해당 포스팅은 프로그래머스 Lv.2 소수찾기 풀이를 다룬다. 문제 링크
코드는 javascript로 작성하였으며 재귀와 에라토스테네스의 체로 풀이하였다.

---

풀이

input으로 주어지는 숫자들을 이용해 모든 순열들을 구한 후, 소수인 숫자들의 개수를 구하면 되는 문제이다.

모든 순열을 구하기 위해 재귀와 Set 컬렉션을 이용하고, 소수를 판별하기 위해 에라토스테네스의 체를 이용하였다.

---

로직 & 예제

1. 모든 순열 구하기 : 재귀 이용

input으로 문자열 "135"가 주어졌다고 가정해보자.

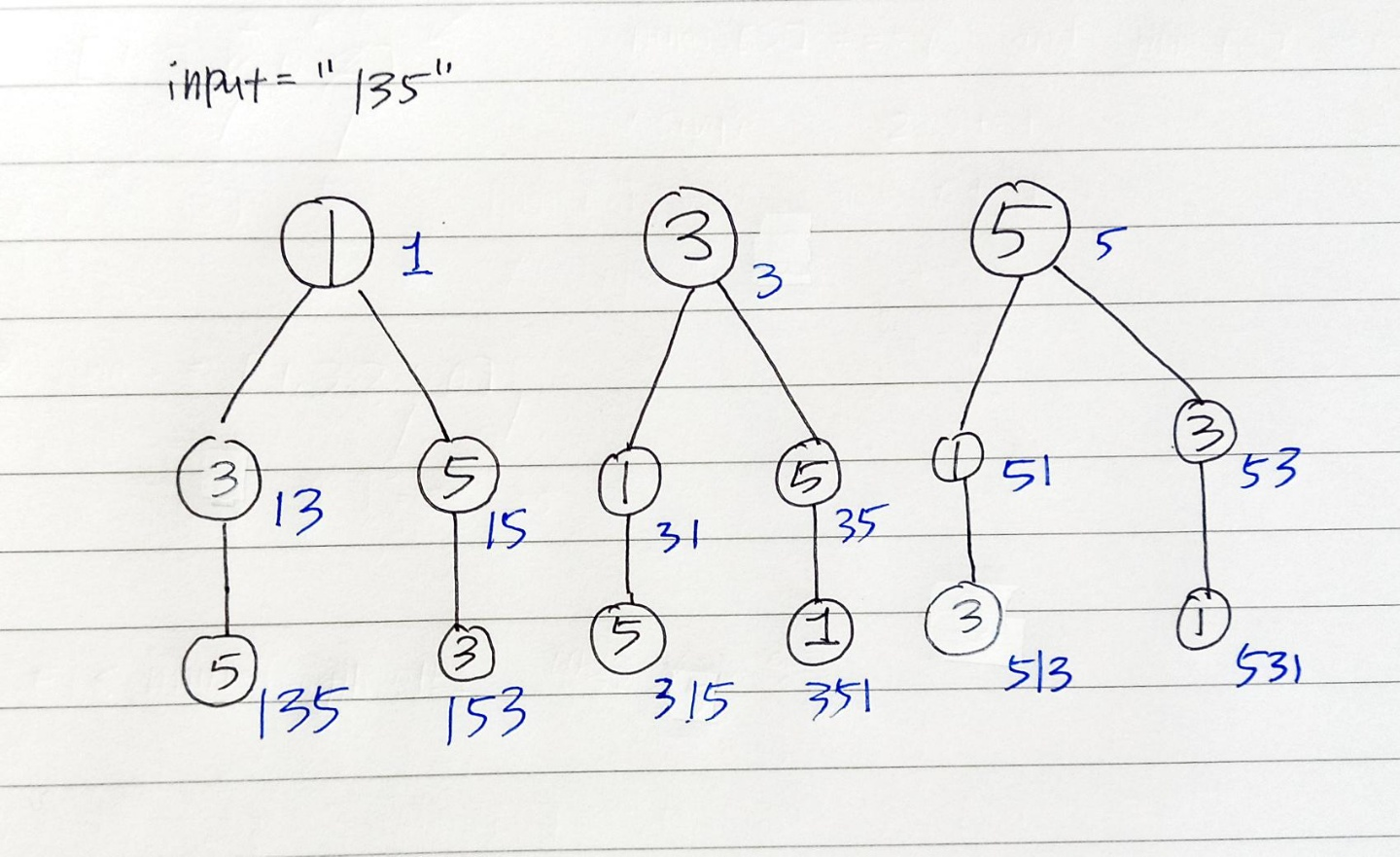
모든 순열을 구하기 위해서는 하나의 숫자를 고정한 다음 그 다음 숫자들을 더해주면 된다. 위의 사진처럼 일종의 트리를 만든다고 생각하면 되는데 DFS 로직과 흡사하다.

아래 코드를 보자.

const permutation = new Set();

makePermutation('', numbers);

// 모든 순열 구하기
function makePermutation(perm, others) {
    if (perm !== '') {
        permutation.add(Number(perm));
    }
    for (let i=0; i < others.length; i++) {
        const remove_i_others = others.substr(0,i) + others.substr(i+1);
        makePermutation(perm + others[i], remove_i_others);
    }
}

재귀함수인 makePermutation은 매개변수로 이전에 생성한 순열 perm과 그 다음 더해줄 숫자 others를 받는다.

input으로 문자열 "135"를 받았다고 가정해보자. 처음 재귀함수를 호출할 때는 아직 이전의 순열이 만들어지지 않은 상태이다.

즉 첫 재귀함수 호출로 아직 만든 순열이 없다. 따라서 perm은 빈 문자열, others는 "135"를 전달해준다 makePermutation('', '135').

함수를 호출하면 perm은 빈 문자열이므로 순열 리스트 Set에 추가하지 않는다.

이제 for loop를 돌리면서 각 숫자를 root로 트리를 생성할 것이다.

그리고 그 다음 순열들을 구하기 위해 각 root 숫자와, root를 제외한 나머지 숫자들을 인자로 전달해 재귀함수를 호출한다. 그럼 아래의 재귀함수가 호출된다.

makePermutation('1', '35')
makePermutation('3', '15')
makePermutation('5', '13')

각 재귀함수가 호출이 되면 이전에 생성한 perm인 1,3,5가 순열 리스트 Set에 추가된다.

이러한 과정들을 전부 거치면 아래의 트리들이 생성이 된다. 즉 모든 재귀함수 호출 종료 시 순열 Set은 { 1, 13, 135, 15, 153, 3, 31, 315, 35, 351, 5, 51, 513, 53, 531 }이 된다.

---

2. 순열 중 소수인 값들만 추려내기 - 에라토스테네스의 체

문제에서 순열 Set 중 소수인 것들의 개수를 구하라고 나와있다. 순열 Set 중 가장 값이 큰 원소에 대해 에라토스테네스의 체를 이용하자.

const max_permutation = Math.max(...permutation_arr);
const primeNumberSieve_of_max = primeNumberSieve(max_permutation);

// 에라토스테네스의 체
function primeNumberSieve(n) {
    const arr = new Array(n+1);
  	for (let i = 2; i <= n; i++) {
        arr[i] = i;
    }
   	
    for (let i = 2; i <= n; i++) {
        if (arr[i] === 0) continue;
        for (let j = i * 2; j <= n; j += i) {
            arr[j] = 0;
        }
    }
    
    const prime = arr.filter(el => el !== 0);
    return prime;
}

순열 Set에서 가장 큰 값은 531이다. 따라서 primeNumberSieve_of_max은 1부터 531까지의 수 중 소수들의 list이다.

이제 순열 Set에 소수들이 몇 개 존재하는지 확인하기 위해 filter를 이용해 permutation_arr와 primeNumberSieve_of_max의 교집합을 구해준다. 그 다음 교집합의 길이를 리턴해주면 된다.

// 순열 list와 소수 list의 교집합
const permutation_primeArr = permutation_arr.filter(num => {
  return primeNumberSieve_of_max.includes(num);
});

return permutation_primeArr.length;

---

전체 코드

const permutation = new Set();

function solution(numbers) {
    makePermutation('', numbers);
    
    const permutation_arr = Array.from(permutation);
    const max_permutation = Math.max(...permutation_arr);
    
    const primeNumberSieve_of_max = primeNumberSieve(max_permutation);
    const permutation_primeArr = permutation_arr.filter(num => {
        return primeNumberSieve_of_max.includes(num);
    });
    
    return permutation_primeArr.length;
}


function makePermutation(perm, others) {
    if (perm !== '') {
        permutation.add(Number(perm));
    }
    for (let i=0; i < others.length; i++) {
        const remove_i_others = others.substr(0,i) + others.substr(i+1);
        makePermutation(perm + others[i], remove_i_others);
    }
}


function primeNumberSieve(n) {
    const arr = new Array(n+1);
  	for (let i = 2; i <= n; i++) {
        arr[i] = i;
    }
   	
    for (let i = 2; i <= n; i++) {
        if (arr[i] === 0) continue;
        for (let j = i * 2; j <= n; j += i) {
            arr[j] = 0;
        }
    }
    
    const prime = arr.filter(el => el !== 0);
    return prime;
}