해당 포스팅은 동빈나 실전 알고리즘 강좌를 보고 정리한 것입니다. 다른 소수판별 알고리즘과 에라토스테네스 체를 비교한 다음, 언제 에라토스테네스 체를 사용해야 하는지를 서술하고자 합니다.

---

에라토스테네스의 체?

에라토스테네스의 체는 가장 대표적인 소수판별 알고리즘이다. 해당 알고리즘은 소수를 대량으로 빠르고 정확하게 구하기 위해 사용된다. 그럼 에라토스테네스의 체를 공부하기 전 소수를 판별하는 알고리즘을 짜보자.

소수판별 알고리즘

1. 판별하려는 수까지 나누어보기: O(N)

function isPrimeNumber(n) {
    for (let i = 2; i < n; i++) {
        if (n % i === 0) return false;
    }
    return true;
}

isPrimeNumber(97) // true

위 알고리즘은 2부터 판별하려는 수까지, 모든 수를 돌면서 소수인지 판단한다. 해당 알고리즘의 시간 복잡도는 O(N)이다. 해당 알고리즘은 판별하고자 하는 수의 제곱근까지 확인하므로써 O(N^(1/2))로 손쉽게 계산할 수 있다.

2. 판별하고자 하는 수의 제곱근까지 나누어보기: O(N^(1/2))

function isPrimeNumber(n) {
    for (let i = 2; i**2 < n; i++) {
        if (n % i === 0) return false;
    }
    return true;
}

isPrimeNumber(97)

위 알고리즘은 판별하고자 하는 수의 제곱근까지 돌면서 소수인지 판단한다. 원리는 모든 약수가 가운데 약수(제곱근)를 기준으로 곱셈 연산에 대해 대칭을 이룬다는 것이다. 예를들어 80의 약수는 아래와 같다.

예제: 80의 소수판별

80의 약수는 1, 2, 4, 5, 8, 10, 16, 20, 40, 80가 있다. 이 때 8 x 10 = 10 x 8은 대칭이다.

• √80은 대략 8.xxxx로, 80의 약수들의 중간값이다.
• 따라서 우리는 특정한 자연수의 모든 약수를 찾을 때 제곱근까지만 확인하면 된다.
  • 예를 들어 80이 8로 나누어떨어진다는 것은 10으로도 나누어떨어진다는 것이다.

---

대량의 소수를 판별할 때 사용하는 에라토스테네스 체

다만 위의 알고리즘처럼 한 두어개 소수를 판별하는 것이 아니라 대량의 소수를 한꺼번에 판별하고자 할 때는 에라토스테네스의 체가 효율적이다.

에라토스테네스의 체는 가장 먼저 소수를 판별할 범위만큼 배열을 할당 후 그 인덱스에 해당하는 값을 넣어준다.

예를 들어 1부터 25까지 판별한다고 가정해보자.

에라토스테네스 체 예시

1부터 25까지의 수 중에서 소수인 수가 뭐가 있는지를 판별해보자.

1. 이차원 배열을 생성하여 값을 초기화한다.

   

2. 2부터 시작하여 특정 숫자의 배수에 해당하는 숫자들을 모두 지운다.

   • 먼저 2의 배수를 지우자(자기 자신은 지우지 않습니다).
     

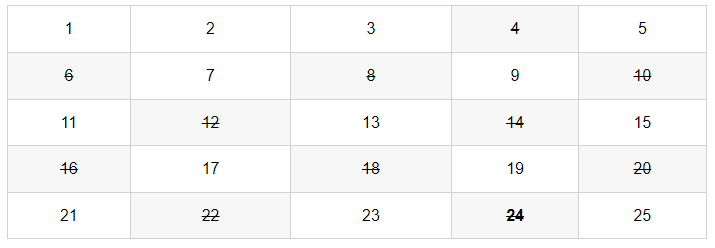
   • 이제 3의 배수를 지우자(자기 자신은 지우지 않습니다).
     

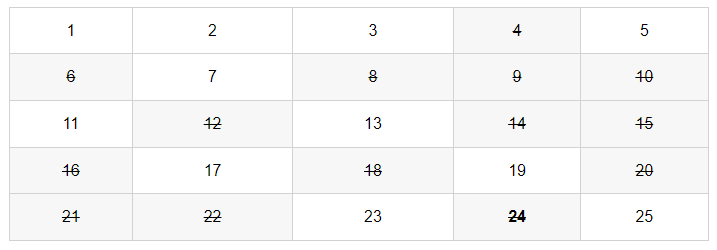
3. 이미 지워진 숫자의 경우 건너뛴다.

   • 4는 이미 지워졌으므로 건너뛴다. 이제 이러한 과정을 반복한다.
     

4. 2부터 시작하여 남아있는 숫자들을 출력한다.
   

출력: 2 3 7 11 13 17 19 23

이러한 과정을 JS 소스코드로 옮겨보자.

function primeNumberSieve(n) {
    const arr = new Array(n+1);
    // 인덱스에 해당하는 값 채우기
  	for (let i = 2; i <= n; i++) {
        arr[i] = i;
    }
   	
  	// 약수 여부 확인하기
    for (let i = 2; i <= n; i++) {
        if (arr[i] === 0) continue;
        for (let j = i * 2; j <= n; j += i) {
            arr[j] = 0;
        }
    }
    
  	// 소수인 값 넣어주기
    const prime = arr.filter(el => el !== 0);
    return prime;
}

primeNumberSieve(25); // [2, 3, 5, 7, 11, 13, 17, 19, 23]

에라토스테네스의 체는 시간복잡도가 O(Nlog(logN)) 으로 가장 빠르고 정확하게 소수를 구하는 알고리즘이다.