[알고리즘] 크루스칼 알고리즘(Kruskal Algorithm)

크루스칼 알고리즘(Kruskal Algorithm)

크루스칼 알고리즘은 그래프에서 최소 비용 신장 부분 트리(최소 신장 트리: Minimum Spanning Tree)를 찾는 알고리즘이다.

매커니즘

• 크루스칼 알고리즘은 기본적으로 그리디한 선택을 바탕으로 알고리즘을 진행한다.

1. 주어진 그래프의 모든 간선에 대해, 간선의 연결비용을 낮은 순으로 오름차순 정렬한다.
2. 정렬된 간선 순서대로 선택하면서, 간선의 양 끝 정정을 Union 한다. 단, 이때 선택된 두 정점이 같은 집합에 속해있다면 사이클(cycle)이 있다고 판단하여 포함시키지 않는다)

• 이러한 매커니즘을 바탕으로 최종 선택된 간선을 연결하는 것이 최소 비용 신장트리이다.

과정

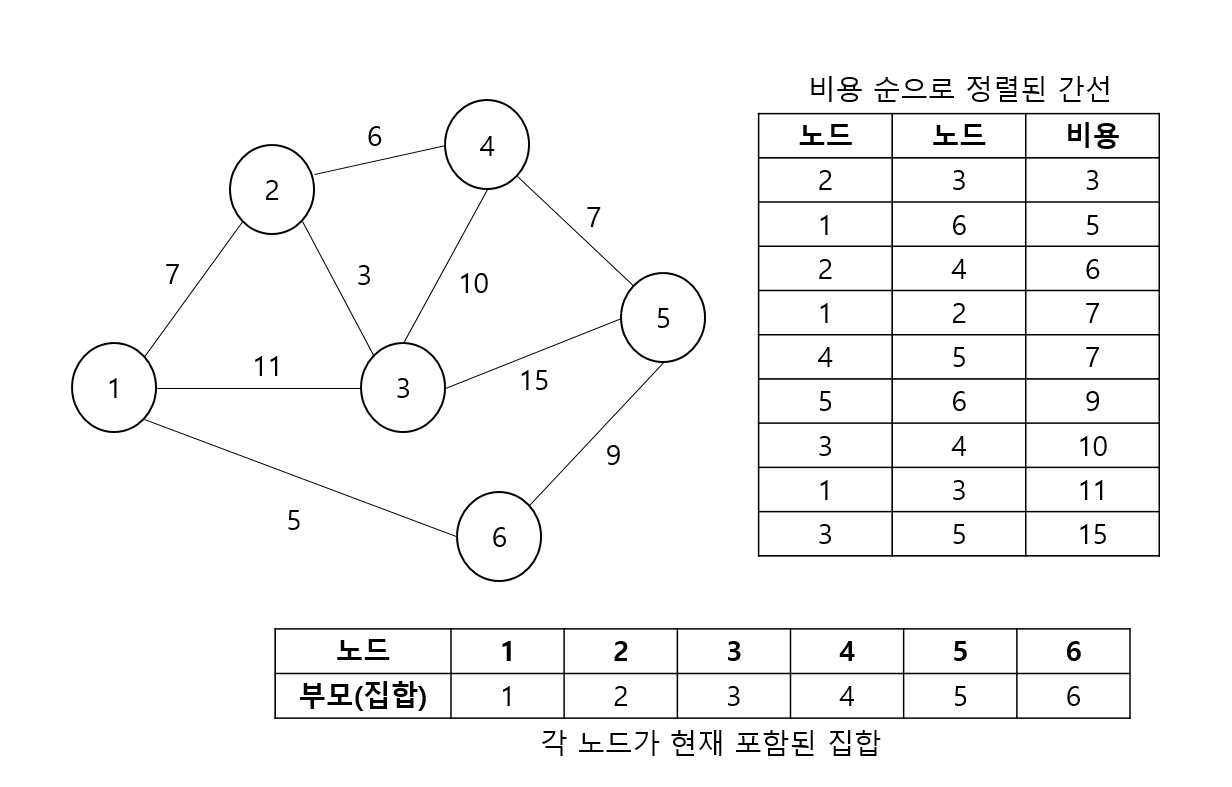
• 비용이 적은 간선의 양 끝 노드를 선택하고 사이클이 존재하지 않는다면 Union 및 해당 간선 선택, 존재한다면 스킵하는 형태로 모든 간선에 대하여 탐색이 끝날 때까지 동작을 반복한다.

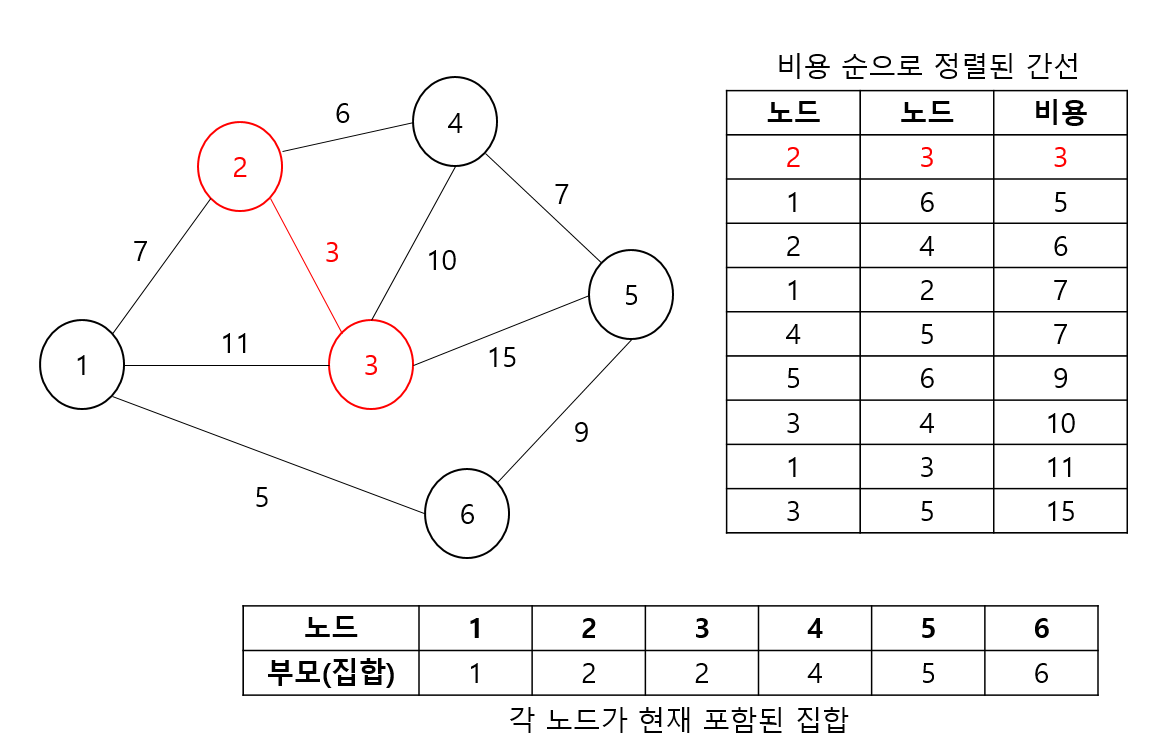
• 먼저 첫번째 간선을 선택한다. 두 노드 2,3은 서로 독립된 집합이기 떄문에 Union을 진행하고 간선도 선택한다.

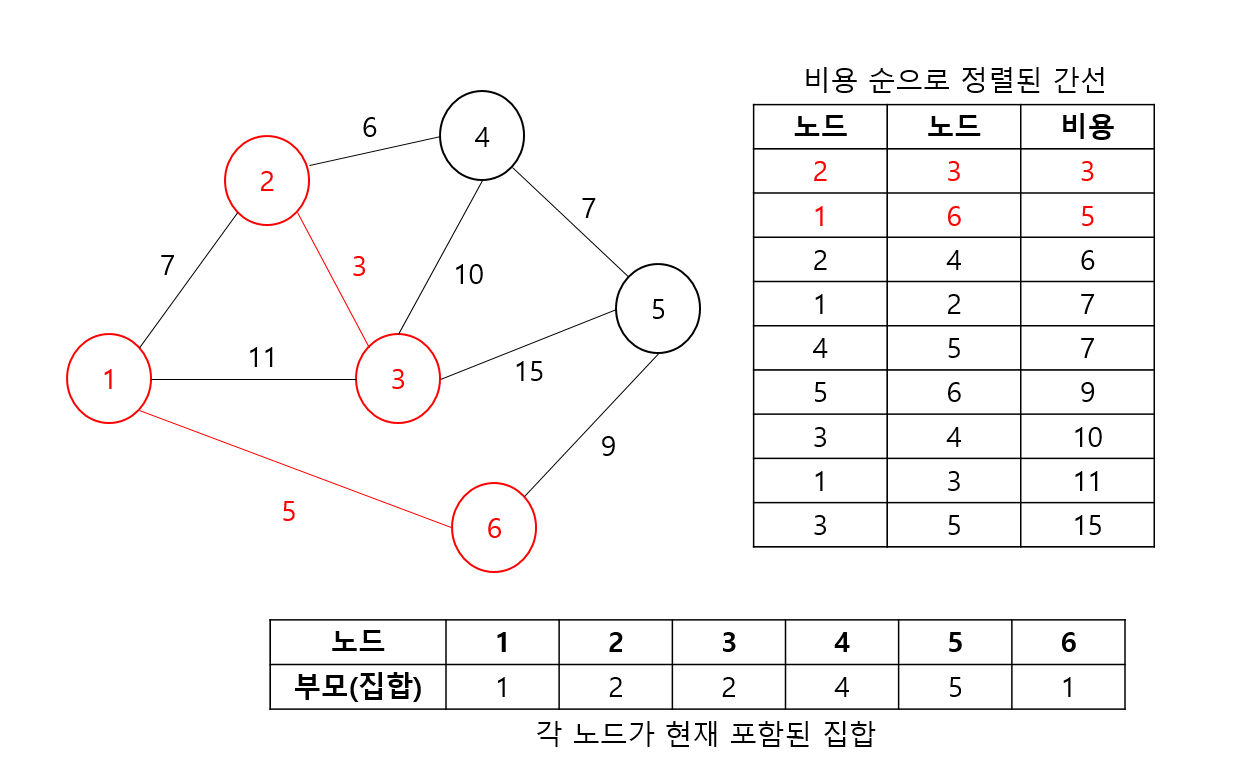
• 마찬가지 방법으로 두번쨰 간선을 선택한다. 두 노드 1,6은 서로 독립된 집합이므로 Union 및 간선을 선택한다.

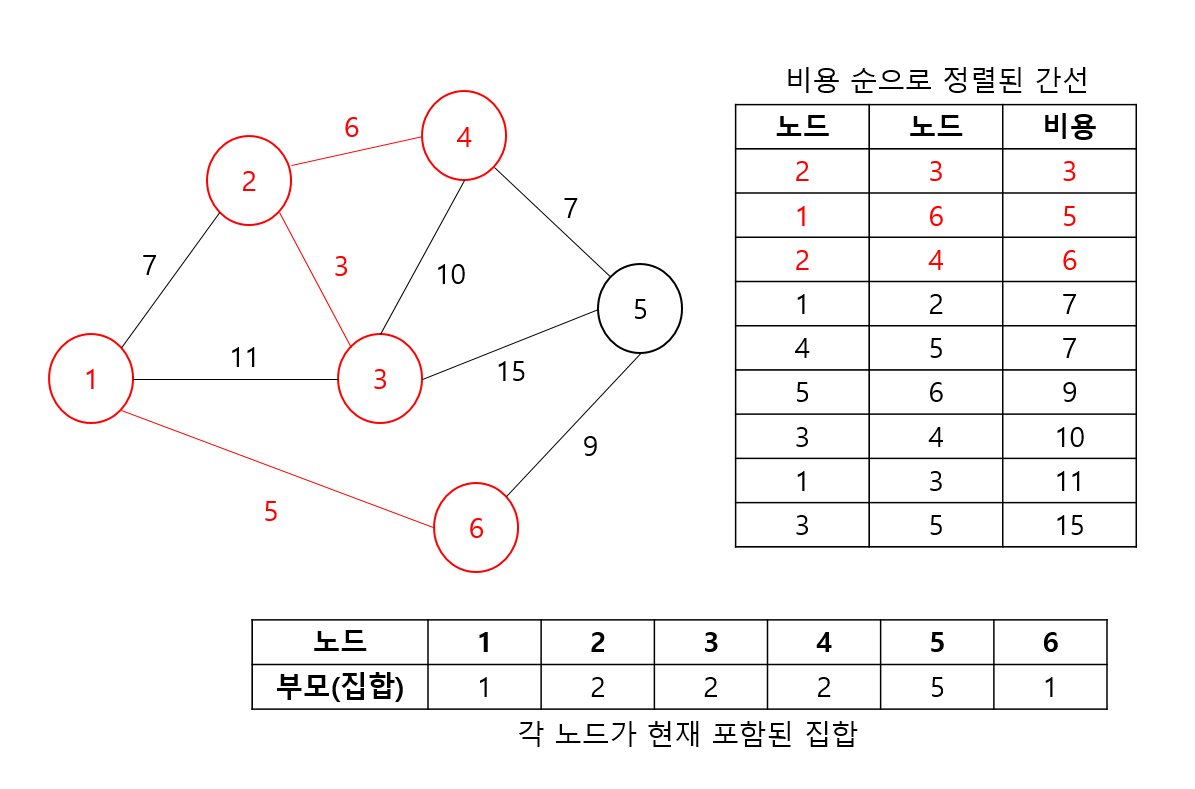
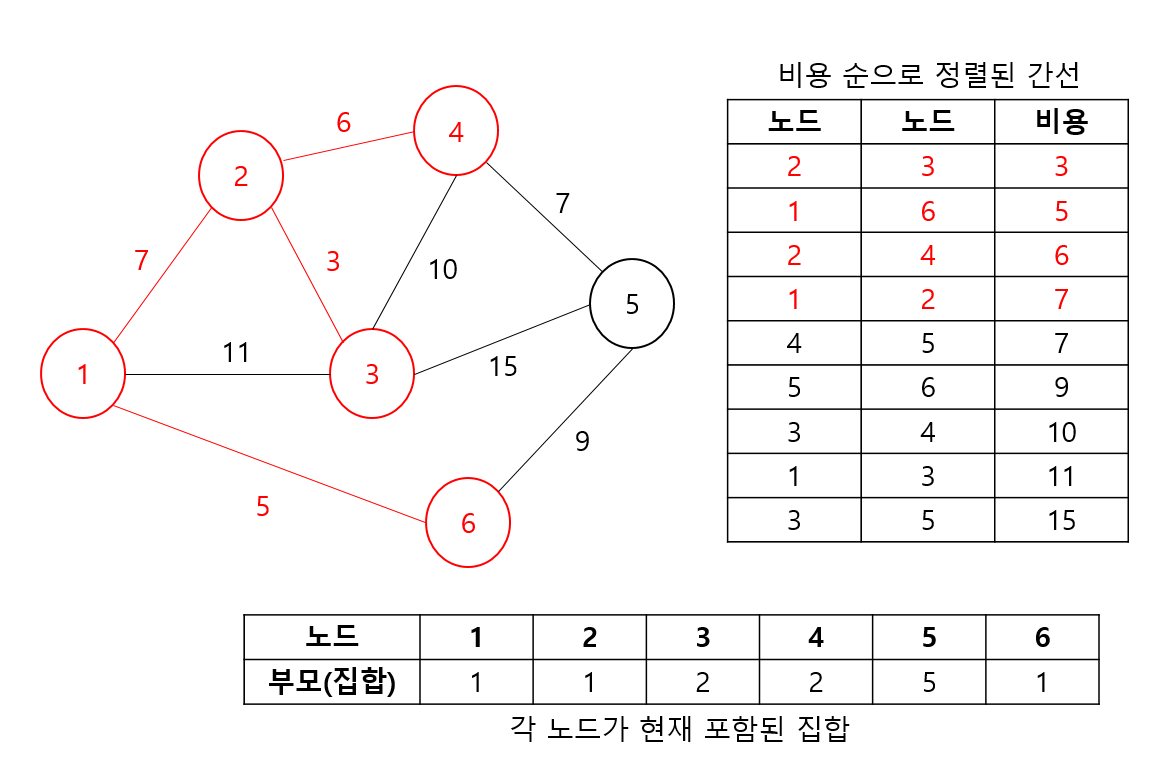
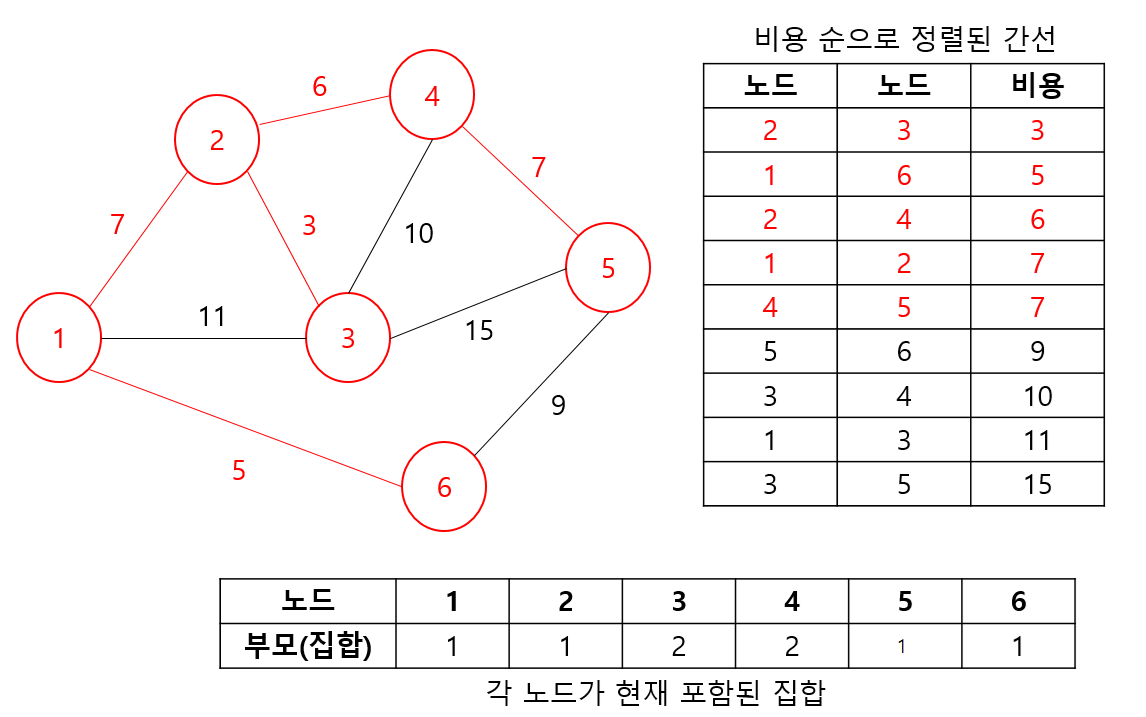
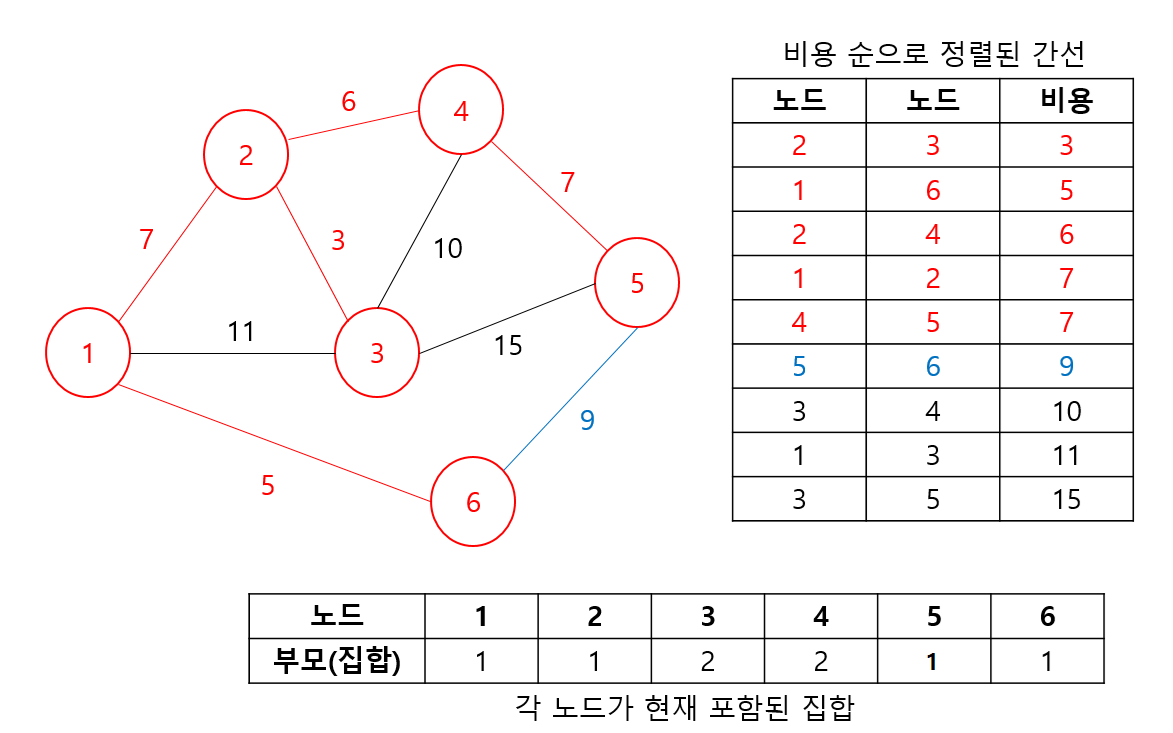
• 5, 6번 노드를 간선에 대해서는 각 노드 5번의 최종 부모는 1, 6번의 최종 부모는 1로 두 집합은 이미 같은 집합에 속해있음을 알 수 있다. 그림에서 확인해보면 알겠지만, 두 노드를 연결하는 순간 사이클이 발생한다. 따라서, 이 경우는 스킵한다.

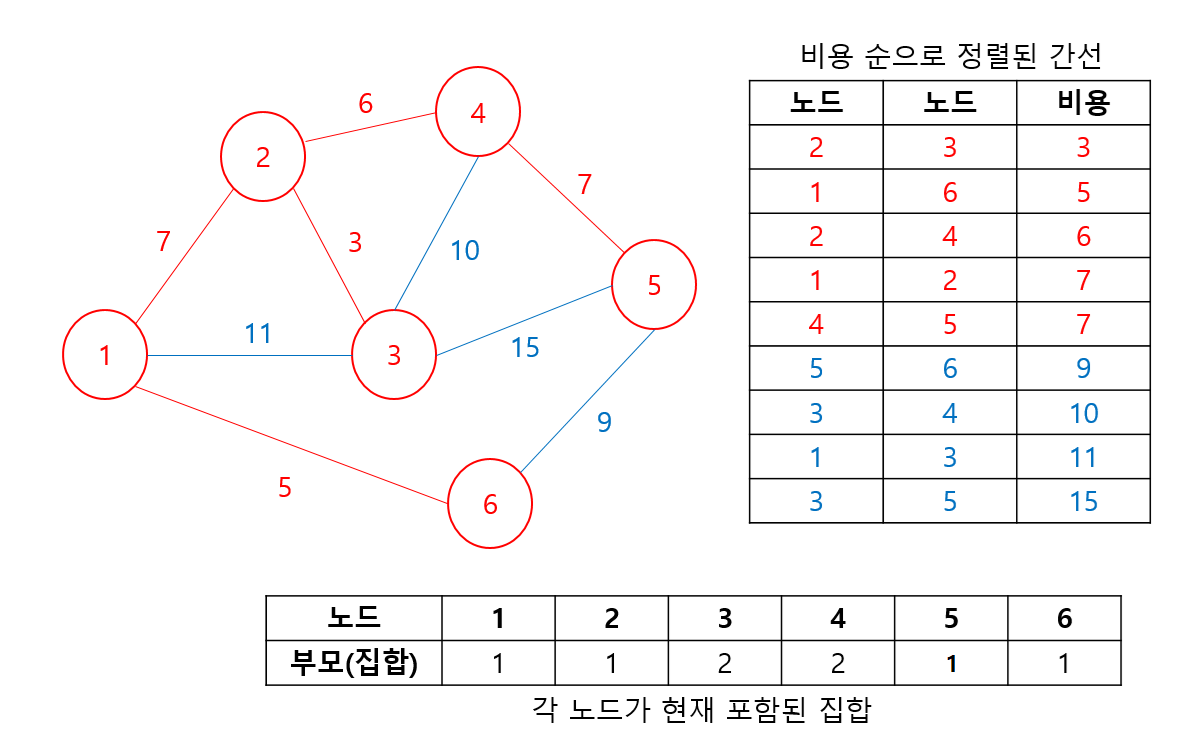
• 나머지 노드에 대해서도 마찬가지로 진행해주면, 최종적으로 선택된 간선(빨간색)이 최소 신장트리(MST)가 됨을 확인할 수 있다.

구현(JAVA)

import java.util.Arrays;
import java.util.Scanner;

/*
sample input(첫 줄의 첫 숫자는 정점의 개수, 두 번째 숫자는 간선의 개수).
6 9
1 6 5
2 4 6
1 2 7
3 5 15
5 6 9
3 4 10
1 3 11
2 3 3
4 5 7
 */

public class Kruskal {
	static int V, E;
	static int[][] graph;
	// 각 노드의 부모
	static int[] parent;
	// 최종적으로 연결된 최소 신장 트리 연결 비용.
	static int final_cost;

	public static void main(String[] args) {
		// 그래프의 연결상태(노드1, 노드2, 비용)를 초기화.
		Scanner sc = new Scanner(System.in);
		V = sc.nextInt();
		E = sc.nextInt();
		graph = new int[E][3];
		for (int i = 0; i < E; i++) {
			graph[i][0] = sc.nextInt();
			graph[i][1] = sc.nextInt();
			graph[i][2] = sc.nextInt();
		}
		parent = new int[V];
		final_cost = 0;

		// 간선 비용 순으로 오름차순 정렬
		Arrays.sort(graph, (o1, o2) -> Integer.compare(o1[2], o2[2]));

		// makeSet
		for (int i = 0; i < V; i++) {
			parent[i] = i;
		}
		// 낮은 비용부터 크루스칼 알고리즘 진행
		for (int i = 0; i < E; i++) {
			// 사이클이 존재하지 않는 경우에만 간선을 선택한다(여기서는 최종 비용만 고려하도록 하겠다).
			if (find(graph[i][0] - 1) != find(graph[i][1] - 1)) {
				System.out.println("<선택된 간선>");
				System.out.println(Arrays.toString(graph[i]));
				union(graph[i][0] - 1, graph[i][1] - 1);
				final_cost += graph[i][2];
				System.out.println("<각 노드가 가리키고 있는 부모>");
				System.out.println(Arrays.toString(parent) + "\n");
				continue;
			}
		}
		
		System.out.println("최종 비용 : " + final_cost);
		sc.close();
	}

	private static void union(int a, int b) {
		a = find(a);
		b = find(b);
		if (a > b) {
			parent[a] = b;
		} else {
			parent[b] = a;
		}
	}

	private static int find(int x) {
		if (parent[x] == x)
			return x;
		else
			return find(parent[x]);
	}
}