point !

구간합 알고리즘을 사용하기 위해서는 합 배열을 구해야 합니다

배열 A가 있을 때 합 배열 S는 다음과 같이 정의합니다

S[i] = A[0] + A[1] + A[2] + ... + A[A-1] + A[i]

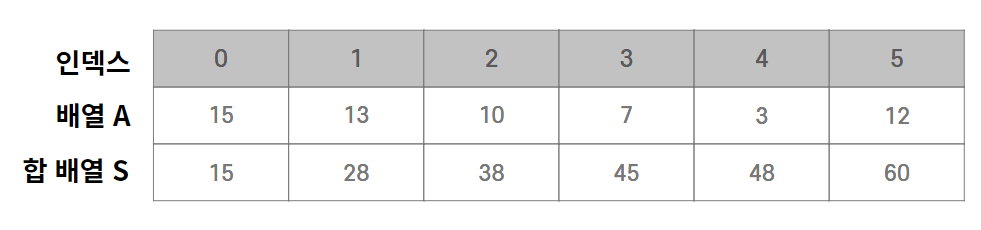
합 배열은 기존의 배열을 전처리한 배열이라고 생각하면 됩니다

합 배열을 미리 구해두면 일정 범위의 합을 구하는 시간복잡도가 O(N) 에서 O(1) 로 바뀝니다

• A[i] 부터 A[j]까지의 배열 을 합 배열 없이 구하는 경우

  최악의 경우 i가 0, j가 N인 경우로 시간 복잡도는 O(N) 입니다

  이런 경우 힙 배열을 사용하면 O(1) 안에 답을 구할 수 있습니다

합 배열 S를 만드는 공식

S[i] = S[i-1] + A[i]

위 공식을 사용하여 구간 합 역시 쉽게 구할 수 있습니다

구간 합 구하는 공식

S[i] - S[i-1]

예제

A[2] 에서 A[5] 까지의 구간 합을 구간 합 배열을 통해 구해보겠습니다

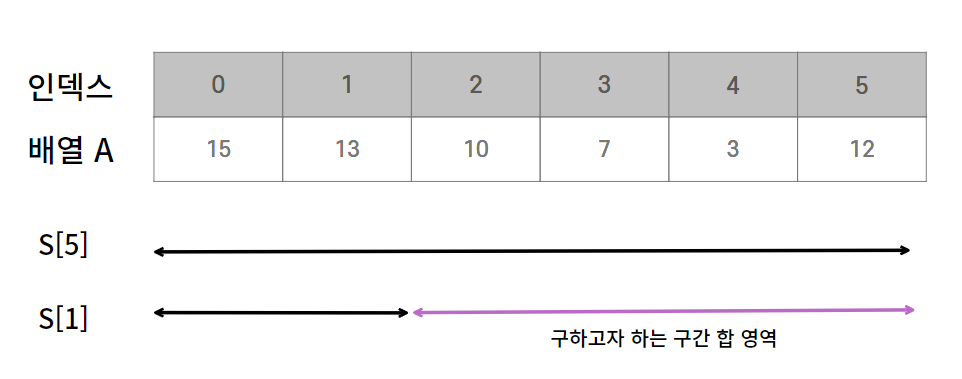
힙 배열과 구간합이 연관되어 있다는 것을 알 수 있습니다

A[0] + ... A[5]에서 A[0] + A[1]을 빼면 구간 합 A[2] + ... + A[5] 가 나오므로

S[5]에서 S[1]을 빼면 구간 합을 구할 수 있습니다