📚 Array

Array는 연관된 data를 메모리상에서 연속적이며 순차적으로 미리 할당된 크기만큼 저장하는 자료구조 이다.

📌 Array의 특징

• 고정된 저장 공간(fixed-size)
• 순차적인 데이터의 저장(order)

⏱ Time complexity (시간 복잡도)

• 조회(look up) : O(1) , random access
• 마지막 인덱스에 추가(append) : O(1)
• 마지막 인덱스에 삭제: O(1)
• 삽입(insert) : O(n)
• 삭제(delete) : O(n)
• 탐색(search) : O(n)

만약 3번째의 인덱스에 저장되어 있는 데이터를 조회 하고자 할때 컴퓨터는 1번 인덱스의 데이터부터 순차적으로 접근 하면서 조회 해야 할까?

Array는 순차적으로 데이터가 저장되어 있기 때문에
첫번째 인덱스의 주소값(0X4AF51) + (4 * 3) = 0x4AF6D
계산을 통해서 바로 구할 수 있다. 이것을 random access 라고 한다.

인덱스의 주소 정보를 계산으로 바로 구할 수 있고 마지막 인덱스 한번의 계산으로 주소 접근이 가능하기 때문에 시간 복잡도가 O(1) 이다.

삽입, 삭제, 탐색의 시간 복잡도가 0(N)으로 정해지는 이유는 Array가 메모리 상에서 순차적으로 저장 되어있어야 하기 때문이다.

만약 새로운 데이터 5가 추가 된다고 가정했을때

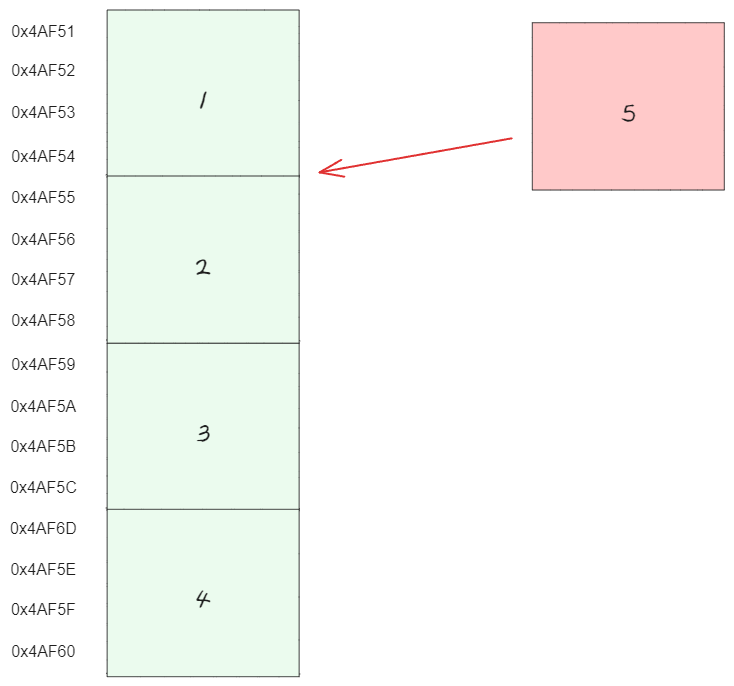
인덱스부터 배열 끝까지의 모든 원소를 한 칸씩 뒤로 밀어야 한다. 따라서 이 동작의 시간 복잡도는 배열의 길이에 비례될 것 이다.

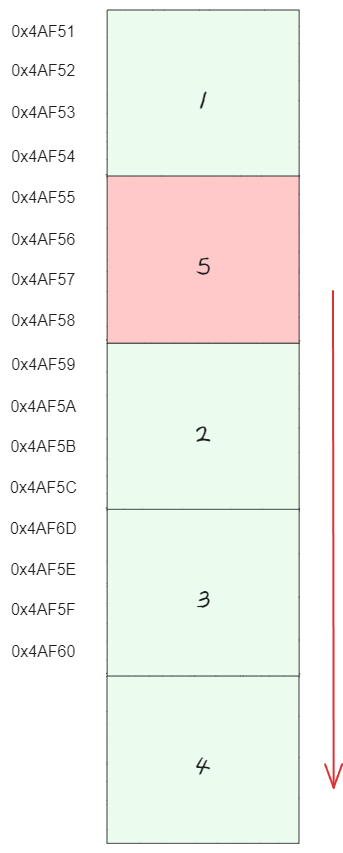
즉, 공간이 4인 배열에서 2번째 인덱스에 5를 넣고 나머지 값을 뒤로 밀어서 5의 공간 Array를 만든다면, 이는 총 3번의 연산(2번째, 3번째, 4번째 원소를 뒤로 밀고, 2번째 위치에 5를 넣는 동작)이 필요하므로 시간 복잡도는 O(3)으로 볼 수 있다.

하지만 단순히 이 경우에 한정된 것이고, 일반적인 경우에는 worst case 복잡도인 O(n)이 될 것이다.

탐색의 경우 컴퓨터는 메모리 주소 계산을 통해 인덱스에는 접근 할 수 있지만 저장되어 있는 값 까지 알 수 있는 것은 아니다.
따라서 결국 모든 배열을 전부 접근해서 찾아야 하기 때문에 배열 길이만큼의 시간 복잡도를 가지게 되는 것이다.

🤔 장단점

리스트의 인덱스를 통한 조회가 자주 필요한 작업에서는 Array 자료구조를 선택하여 적용하는 게 장점으로 작용 될 수 있을 것 같다.

Array의 가장 큰 단점은 데이터 공간이 선언 시에 정해진다는 것이다.

만약 데이터 공간을 50으로 선언하고 개발자가 10개의 공간만을 사용한다면 40개의 공간은 사용되지 않고 낭비 되고 있을 것이다.

한정된 공간을 선언하고 사용하기 때문에 Array 용량을 넘어서는 데이터를 저장이 불가능 하다.

📚 Dynamic Array

그렇다면 용량보다 많은 데이터를 저장할 방법이 없을까?

단순하게 더 큰 용량을 가진 Array를 선언 해주면 기존의 용량보다 많은 데이터를 옮길 수 있을 것이다.

Dynamic Array는 배열 size를 자동으로 resizing 하는 Array 이며 기존에 고정된 size를 가진 Array를 보완하고자 고안 된 자료구조이다.

Dynamic Array는 data의 삽입, 추가로 인해 기존의 할당된 memory 용량을 넘어서게 되면 기존의 size 보다 큰 Array를 선언하고 모든 데이터를 옮긴다.

개발자는 size가 늘어난 Array를 사용 함으로써 추가된 데이터까지 관리 할 수 있는 것이다.

자동으로 memory 초과 시 resizing 하기 때문에 개발자는 size를 미리 고민할 필요가 없다는 장점을 가지게 된다.

그렇다면 Dynamic Array 의 data 를 append 할때 용량이 충분하다면 O(1) 의 데이터 삽입이 가능하지만 만약 용량이 부족해서 resizing 이 발생한다면 data n 개의 이동이 발생 해야한다. 이때의 시간 복잡도가 resize O(n) 이다.

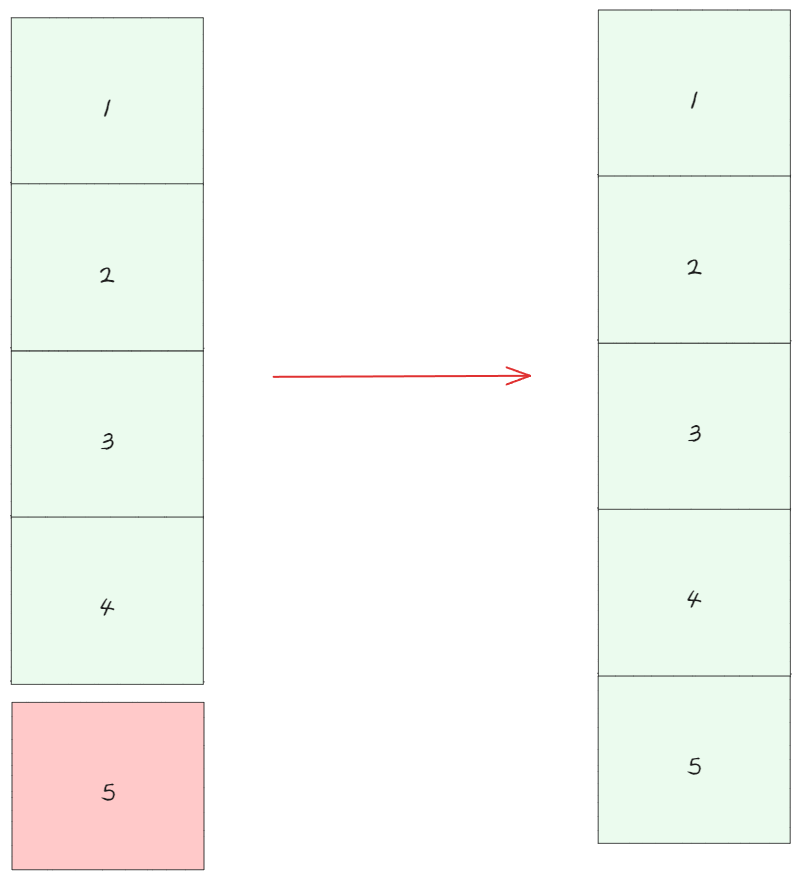
하지만 append의 전체 시간 복잡도는 O(1) or amortized O(1)이다.

물론 worst case 가 O(n)이기 때문에 O(n) 도 맞다고 생각한다.

하지만 거의 대부분의 작업이 O(1)로 처리가 되는데 아주 가끔 O(n)의 상황이 발생한다면 시간 복잡도가 O(n)이라고 말하기 애매 할 것이다.

단순하게 O(n)의 resize 시간을 O(1)의 작업들이 나눠 가짐으로써 전체적으로 O(1)의 시간이 걸린다고 생각하면 이해가 쉬울 것 같다.

💻 resizing

배열의 크기 조정, 즉 resizing에는 다양한 방법이 있다.

그 중에서도 가장 널리 알려진 방법은 Doubling이다.
Doubling은 현재 배열의 용량을 2배로 확장하는 방식이며 새롭게 확장된 배열에 기존의 데이터를 모두 이동하는 과정이 필요하므로, 이 과정에서 O(n)의 시간 복잡도가 발생한다.

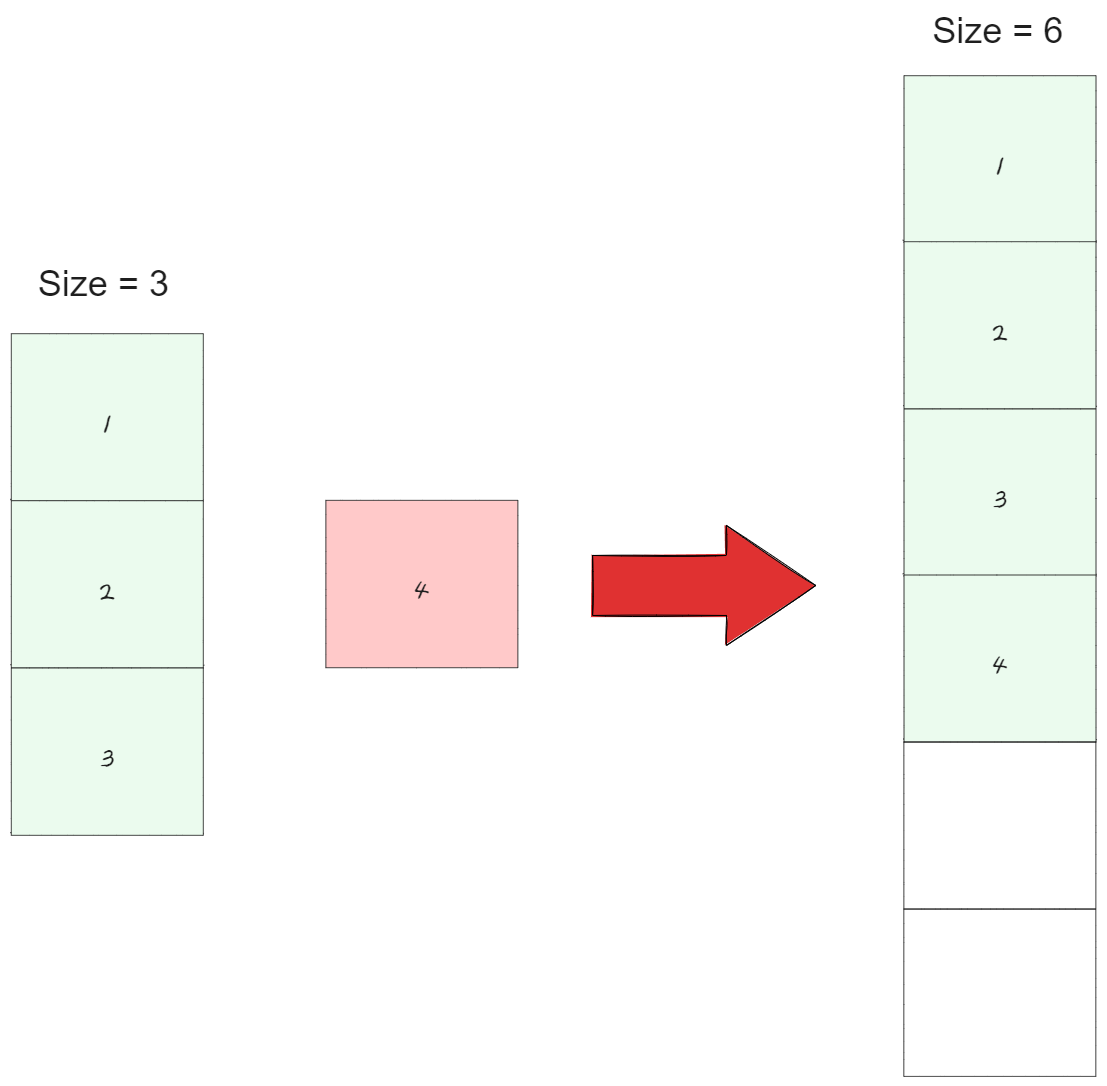
하지만 Doubling 방식에도 단점이 있는데 만약 배열의 크기를 두 배로 늘린 후에 더 이상 데이터 추가나 삽입이 발생하지 않는다면, 그로 인해 발생하는 메모리 낭비가 심해질 수 있다.

이러한 overhead를 줄이기 위한 다양한 방법들이 존재한다.
예를 들어, 일정 개수만큼 배열의 용량을 증가시키는 방법이나, 배열의 용량이 작을 때는 Doubling을, 용량이 큰 상황에서는 일정 개수만큼 용량을 증가시키는 등의 방법이 있을 수 있겠다.

프로젝트의 목적에 따라 적절한 배열 크기 조절 방식을 선택하면, 메모리 사용 효율을 높일 수 있을 것 이라고 생각된다.

🔗 Linked List

Linked List는 Node라는 구조체로 이루어져 있는데, Node는 데이터 값과 다음 Noded의 주소 포인터를 저장 하고 있다.
양방향 Linked List 의 경우 이전 Node의 포인터와 다음 Node의 주소 포인터 모두 저장하고 있다.

Linked List는 물리적인 메모리상에서는 비 연속적으로 저장이 되어있다.

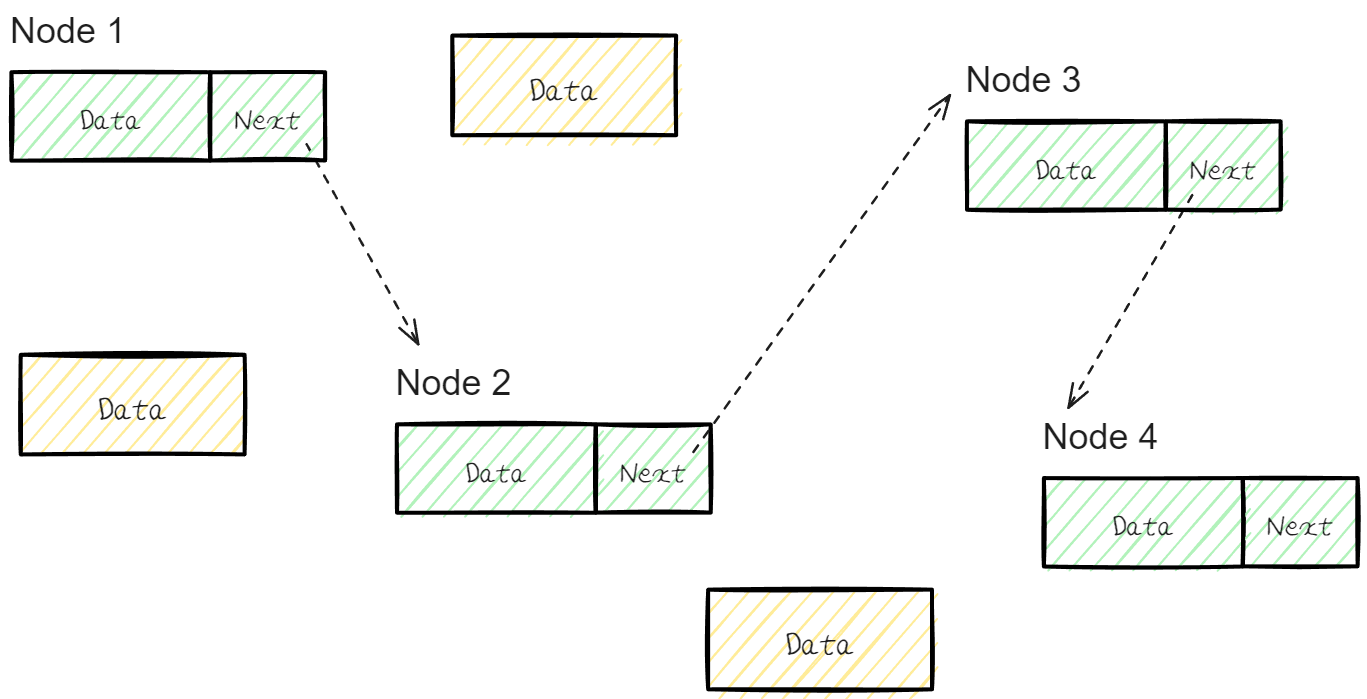
하지만 각각의 Node가 다음 노드의 주소 포인터(address)를 가리킴으로써 접근이 가능하기 때문에 논리적인 연속성을 띄게 된다.

⏱ Time complexity (시간 복잡도)

• 접근(access) : O(n)
• 탐색(search) : O(n)
• 삽입(insert) : O(1)
• 삭제(delete) : O(1)

📌 접근 및 탐색

Array 는 순차적으로 물리적 연결 되어있다고 했다.
하지만 Linked List는 물리적으로 연결 되어 있지 않다.
그렇다면 특정 순번의 Node에 단번에 접근이 불가능 할 것이다.
만약 특정 순번에 Node에 접근을 하려면 가장 처음 Node부터 특정 순번까지 Next Address를 읽어가면서 접근 해야한다.
.

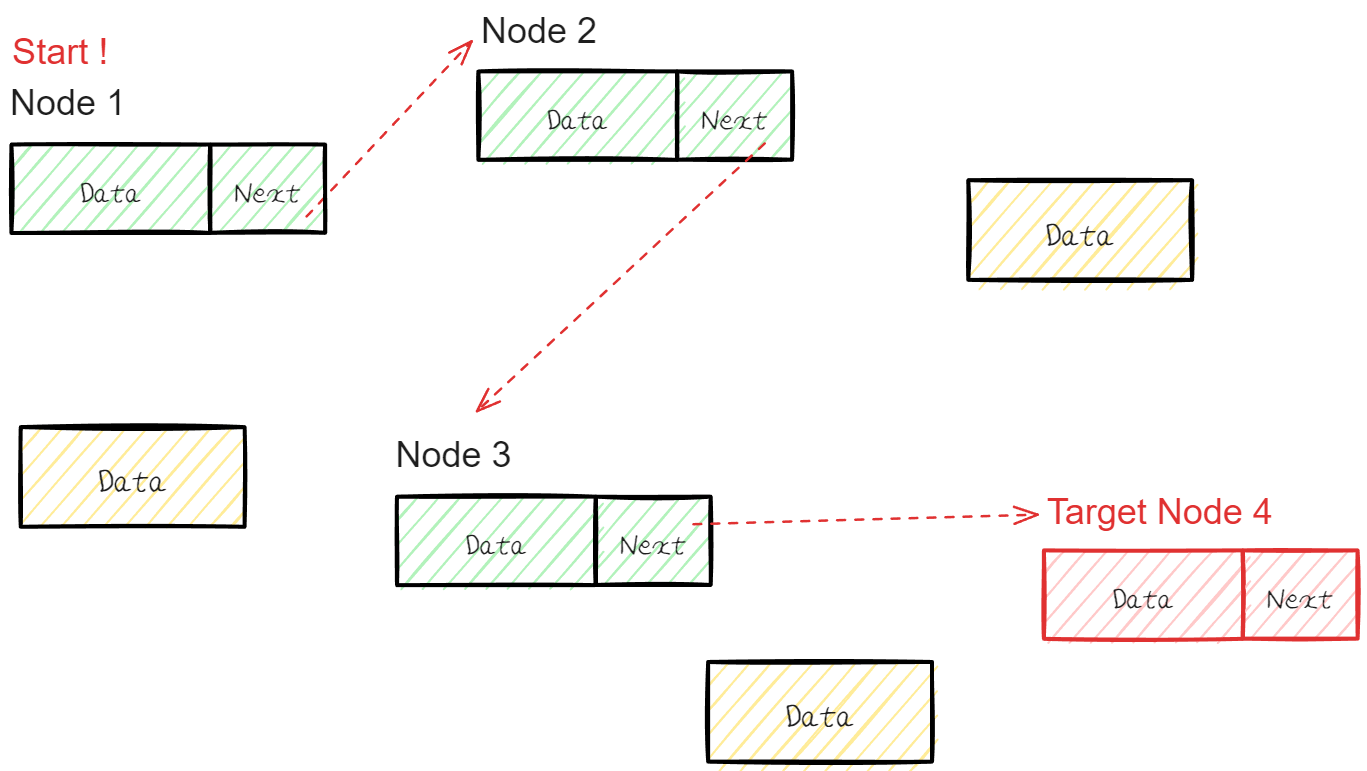
이는 시간복잡도를 증가하게 만드는 원인이다.

📌 삽입

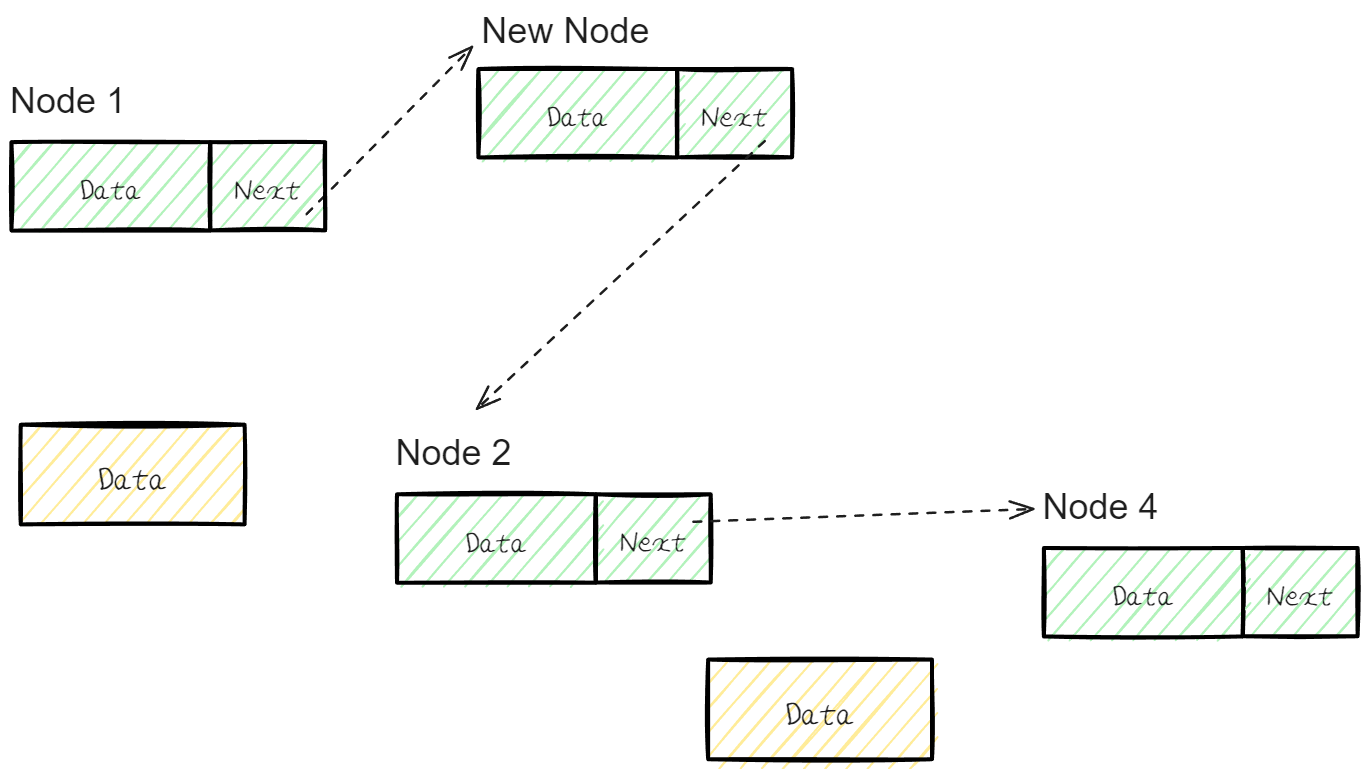
새로운 Node 를 추가한다고 가정해보자.
추가할 Node 는 Node 1과 Node 2의 사이 Node로 Link 되기를 희망하고 있다.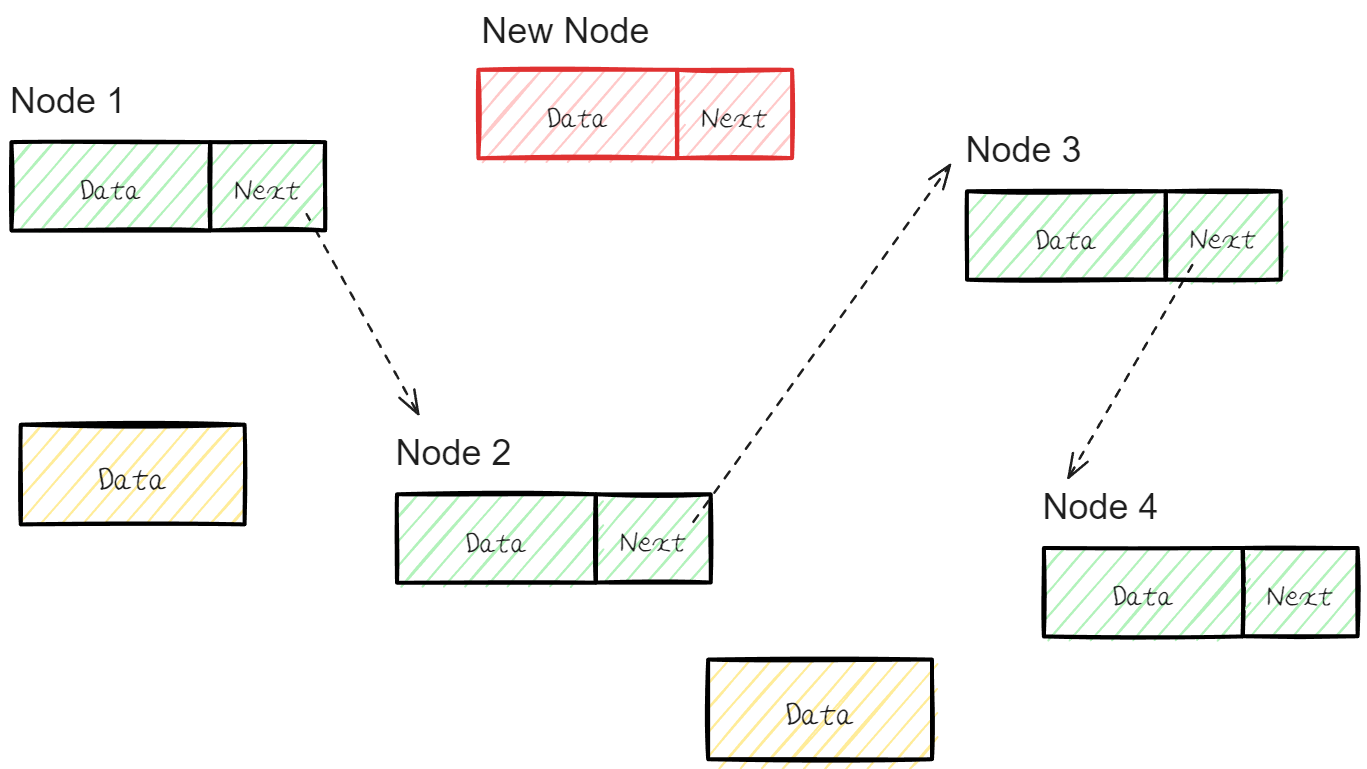
기존의 Node 1의 Next Address를 New Node를 가리키도록 하고 New Node는 기존의 Node 2를 가리키면 정상적인 삽입 절차가 진행 된 것이다.

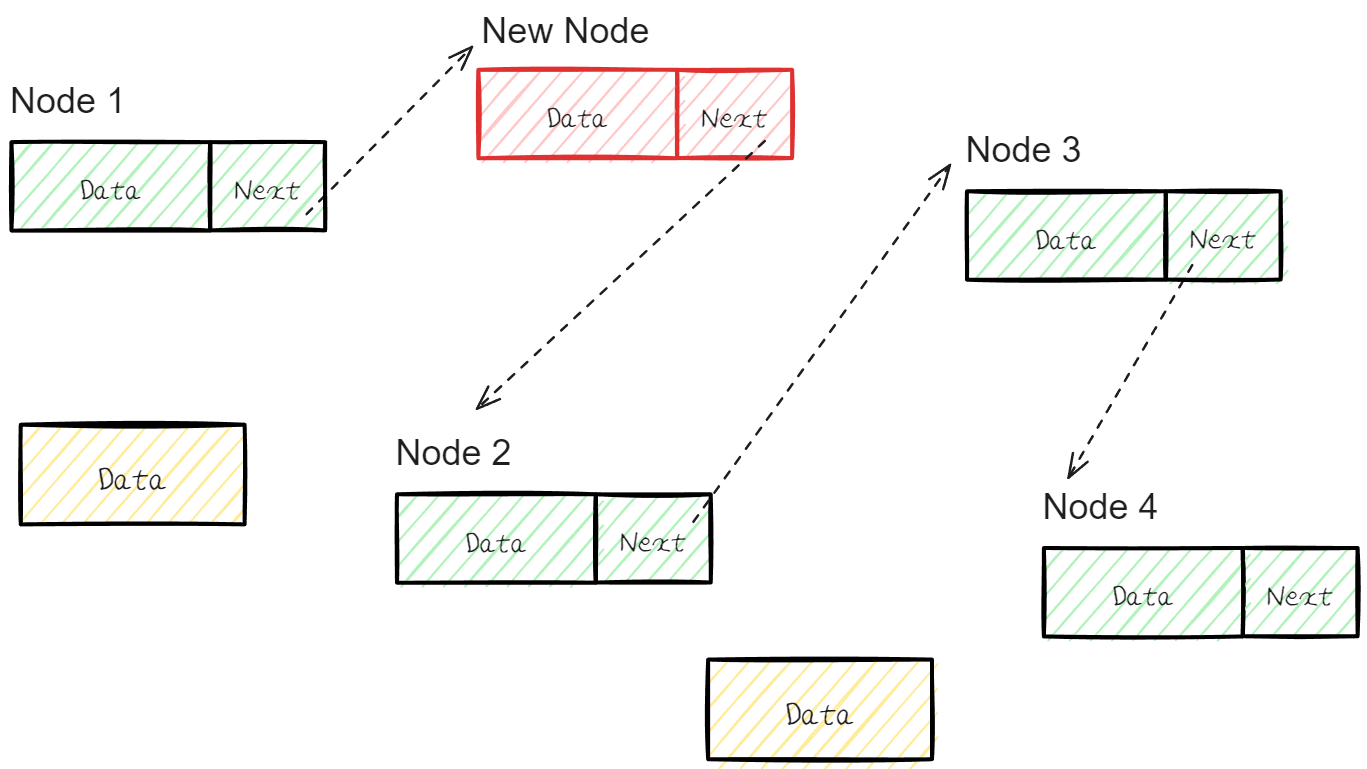
📌 삭제

삭제 역시 간단 하다.
만약 Node 3을 삭제 하고 싶다면 Node 2의 Next Address를 Node 4를 가리키게 해주면 된다

하지만 삽입 또는 삭제의 경우 target Node 를 찾아가는데 까지 Node를 처음부터 거쳐 지나가야 하기 때문에 실질적으로는 O(n)이라고 볼 수 있다.

🙄 비교

Array는 선언 시에 메모리 용량을 확보 한후 생성 되지만 Linked List는 데이터가 추가되는 시점에 메모리를 할당 받기 때문에 메모리를 효율적으로 사용이 가능하다.
하지만 Linked List는 다음 Node를 가리킬 Next Address 포인터 를 저장해야 하기 때문에 데이터 하나당 더 많은 용량을 차지 하게 된다.

따라서 미리 들어올 데이터의 양을 알고 있는 상황에는 Array를 사용하는 것이 더 효율적으로 사용 할 수 있다.

Array는 메모리 상에서 연속적으로 데이터를 저장하지만 Linked List는 물리적으로 연속적이지 않다.
하지만 다음 Node 위치를 Address 포인터 값으로 저장 하고 있기 때문에 논리적으로는 연속성을 가지게 된다.

데이터의 삽입, 삭제의 작업이 잦은 경우에는 시간 복잡도가 O(1)인 Linked List 를, 조회의 작업이 잦다면 Array를 사용하는게 효율적이다.
물론 Linked List는 삽입, 삭제 처리할 위치 까지 탐색 하는 시간 복잡도가 O(n)이다.

🤔 의문점

관련 자료를 좀 찾아보던 중 C언어에서 Array가 Stack 영역에서 저장 된다는 글을 보았다.

Java에서는 Array 와 Linked List가 모두 new 키워드를 통해서 동적 할당 으로 생성되고 Heap 영역에 저장되는 것으로 알고 있었다.
그러나 C 언어에서는 왜 Array가 스택 영역에 저장되는지 의문이 들었다.
그렇다면 C에서는 왜 Array가 Stack 영역에서 저장되는 것일까?

C언어에서 Array는 compile 단계에서 memory 할당이 일어난다. 이를 Static Memory Allocation(정적 메모리 할당)이라고 한다.

Linked List는 개발자의 코드 흐름에 따라 memory 할당이 일어나므로, 이는runtime에 발생 한다.
따라서 Dynamic Memory Allocation(동적 메모리 할당)에 해당 하며 Heap 영역에 저장 되는 것이 맞다.

위 정보를 얻고 Java의 Array가 Heap에 저장 되지 않는 것에 새로운 의문점이 생겼다.

왜 Java의 Array는 Heap에서 저장 되는 것인가?

답은 Java와 C의 차이점에서 발생한다.

C언어에서는 배열의 크기를 선언(compile)할 때 결정한다.

하지만 Java에서는 배열을 선언하는 시점이 아니라, 배열을 실제로 생성하는 시점에 배열의 크기를 결정하기 때문에 runtime으로 취급 받는다.
이는 메모리 공간이 실행 시점에 할당된다는 의미 이기도 하다.

또한 Array는 Java에서 기본 클래스가 아니며 Java에서 구체적인 클래스를 갖는 객체이다.
Java에서 모든 객체는 Heap 영역에서 관리 한다.

따라서 Array를 생성하는 순간 runtime에서 작동하며 객체 이기 때문에 Heap에 저장 되는 것이다.

📗 정리

쉽다 생각하고 넘어 갔던 List를 다시 한번 돌아보게 되었다.
Queue, Stack등 다양한 자료구조를 구현할 때 Linked List를 활용 했기 때문에 List는 나름 잘 알고 있다고 생각했고 자료도 많이 찾아봤었다.

자료를 다시 한번 찾아보면서 Array는 생각보다 몰랐던 상식이 많았다.

Pointer 개념이 Linked List와 다르게 직접적으로는 보여지지 않았기에 단순히 연속성을 띄는 List구나 정도로만 생각 했고 "기초 배열 이구나" 하고 넘어갔기 때문이다.

어쨋든 Array를 통해서 Stack과 Heap에서도 다시 한번 찾아보는 기회 였고 추후 stack과 heap에 대해서 게시글을 한번 써봐야 할 것 같다.
당시 가지고 있던 기술 개념으로 작성된 글 이므로 정확하지 않을 수 있으며 문제가 발견 된다면 수정 하겠습니다.