백준 15681 - 트리와 쿼리 (Java)

장준혁·2024년 4월 2일

Java coding test

coding-test

목록 보기

5/21

🔍 문제

💻 제출

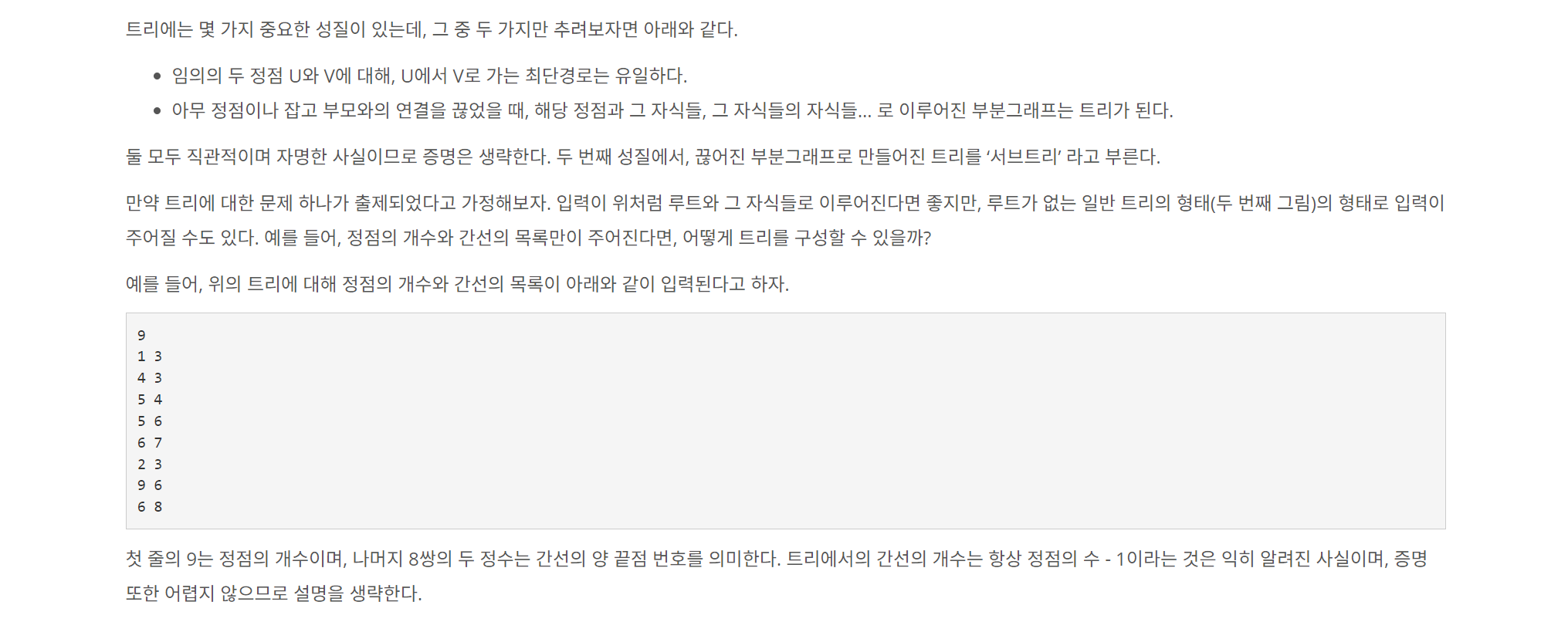
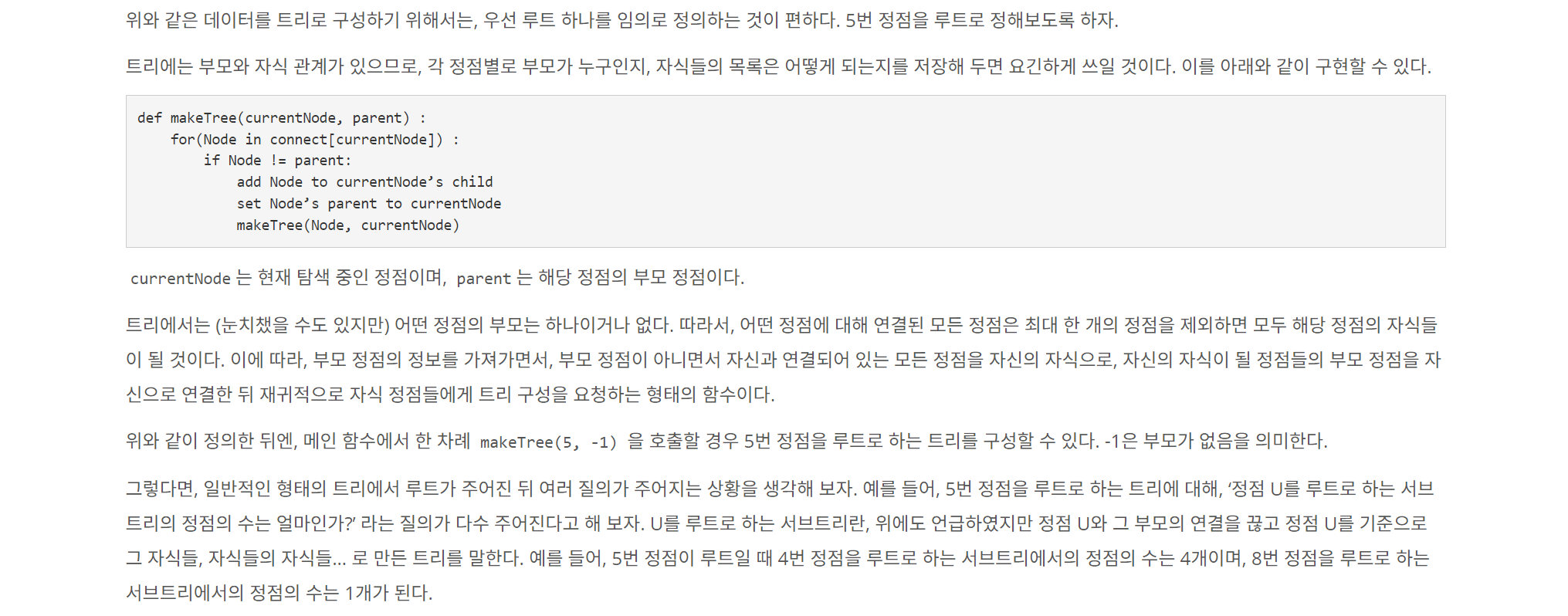
📌 입력

트리의 정점의 수 N과 루트의 번호 R, 쿼리의 수 Q가 주어진다. (2 ≤ N ≤ 105, 1 ≤ R ≤ N, 1 ≤ Q ≤ 105)

이어 N-1줄에 걸쳐, U V의 형태로 트리에 속한 간선의 정보가 주어진다. (1 ≤ U, V ≤ N, U ≠ V)

이는 U와 V를 양 끝점으로 하는 간선이 트리에 속함을 의미한다.

이어 Q줄에 걸쳐, 문제에 설명한 U가 하나씩 주어진다. (1 ≤ U ≤ N)

입력으로 주어지는 트리는 항상 올바른 트리임이 보장된다.

📌 출력

Q줄에 걸쳐 각 쿼리의 답을 정수 하나로 출력한다.

📝 첫번째 코드(메모리 초과)

import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    static int N,R,Q;
    static ArrayList<Integer>[] tree;
    static long[] depth;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        N = Integer.parseInt(st.nextToken()); // 노드 , 정점 개수
        R = Integer.parseInt(st.nextToken()); // 트리의 root 노드 번호
        Q = Integer.parseInt(st.nextToken()); // 질문 개수

        tree = new ArrayList[N+1];
        depth = new long[N+1];

        for (int i=1; i<=N; i++){
            tree[i] = new ArrayList<>();
        }

        for (int i=1; i<=N-1; i++){
            StringTokenizer stD = new StringTokenizer(br.readLine(), " ");

            int s = Integer.parseInt(stD.nextToken());
            int e = Integer.parseInt(stD.nextToken());
            
            tree[s].add(e); //양방향 연결
            tree[e].add(s);
        }

        //root 부터의 depth 기록
        setDepthBfs(R);
        
        for (int i=0; i<Q; i++){ //질문 개수 만큼 순회
            int qRoot = Integer.parseInt(br.readLine());
            long vertexCnt = findVertexBfs(qRoot);

            bw.write(vertexCnt + "\n");
        }

        bw.flush();
        bw.close();
        br.close();
    }

    static void setDepthBfs(int root){ //root 부터의 depth 기록
        boolean[] visited = new boolean[N+1];
        Queue<Integer> q = new LinkedList<>();
        q.offer(root);
        long initD = 0; //root 정점의 깊이는 0
        depth[root] = initD;
        visited[root] = true;

        while (!q.isEmpty()){
            Integer vN = q.poll();
            long cDepth = depth[vN];

            for (int next : tree[vN]){
                if (visited[next] == false){
                    q.offer(next);
                    visited[next] = true;
                    depth[next] = cDepth + 1;
                }
            }
        }
    }

    static long findVertexBfs(int root){ //root 부터의 depth 기록
        long vertexCnt = 1; //정점 포함 1
        boolean[] visited = new boolean[N+1];
        Queue<Integer> q = new LinkedList<>();
        q.offer(root);
        visited[root] = true;


        while (!q.isEmpty()){
            Integer vN = q.poll();
            long cDepth = depth[vN]; //현재 자신의 depth

            for (int next : tree[vN]){
                if (visited[next] == false && cDepth < depth[next]){
                    vertexCnt++;
                    q.offer(next);
                    visited[next] = true;
                }
            }
        }

        return vertexCnt;
    }


}

주어진 root 정점을 통해 각 노드 당 depth 를 배열에 저장한다.
root 정점 = 0 이후 하위 정점 을 +1 하면서 저장한다.
모든 노드에 대한 depth 를 배열에 전부 저장 했다면 이후 주어지는 질문 쿼리의 정점 번호 에 따라 bfs 탐색을 시작한다.

📝 두번째 코드(정상 제출)

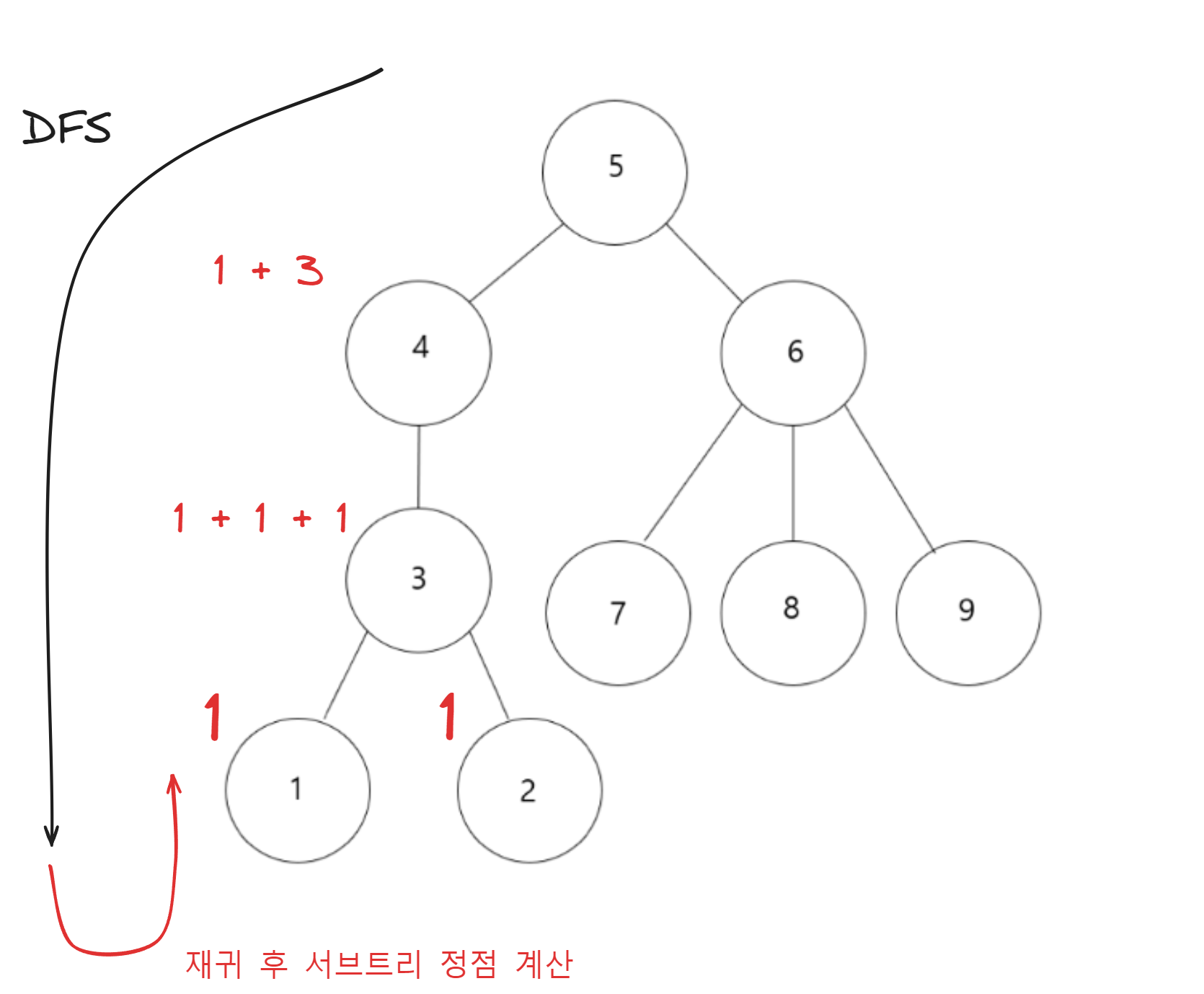
재귀를 마친 후 리프 노드들 부터 root 정점 까지 하위 정점이 몇개 있는 지 확인 하여 계산 했다.

import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;

public class Main {
    static int N,R,Q;
    static ArrayList<Integer>[] tree;
    static long[] subtreeN;
    static boolean[] visited;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");

        N = Integer.parseInt(st.nextToken()); // 노드 , 정점 개수
        R = Integer.parseInt(st.nextToken()); // 트리의 root 노드 번호
        Q = Integer.parseInt(st.nextToken()); // 질문 개수

        tree = new ArrayList[N+1];
        subtreeN = new long[N+1];
        visited = new boolean[N+1];

        for (int i=1; i<=N; i++){
            tree[i] = new ArrayList<>();
        }

        for (int i=1; i<=N-1; i++){
            StringTokenizer stD = new StringTokenizer(br.readLine(), " ");

            int s = Integer.parseInt(stD.nextToken());
            int e = Integer.parseInt(stD.nextToken());
            
            tree[s].add(e); //양방향 연결
            tree[e].add(s);
        }

        dfs(R);
        
        for (int i=0; i<Q; i++){ //질문 개수 만큼 순회
            int qRoot = Integer.parseInt(br.readLine());
            bw.write(subtreeN[qRoot] + "\n");
        }

        bw.flush();
        bw.close();
        br.close();
    }

    static void dfs(int start){ //각 서브트리의 정점 개수 기록
        visited[start] = true; //현재 정점 방문
        subtreeN[start] = 1;

        for (int next : tree[start]){
            if (visited[next] == false){
                visited[next] = true; //다음 정점 visited
                dfs(next);
                subtreeN[start] += subtreeN[next]; //현재 위치의 서브트리 개수에 하위 서브트리 정점 개수를 더해줌
            }
        }
    }


}