
🔍 문제

📌 입력

📌 출력

🤔 문제풀이
해당 문제를 읽었을때 다양한 풀이 방법을 생각했었다.
문제를 해결하기 위해서는 cycle에 들어가지 않는 즉 포함되지 않고 존재하는 정점들의 수를 반환 해주면 된다.
1. DFS를 통해 시작점으로 돌아오는지 전체 탐색
하지만 정점의 개수 N 범위가 굉장히 컷다.
모든 정점을 탐색해서 처음 시작점으로 돌아오는지 확인 해야하기 때문에 시간을 줄이려는 노력이 필요했다.
정점 탐색을 줄이기 위해 한번 발견한 cycle은 따로 DP로 저장해놓고 탐색을 하지 않고 결과를 반환 하는 방법을 고려했다.
하지만 DP로 줄일 수 있는 상황 즉 cycle이 존재하지 않는다면 결국 모든 정점을 탐색 해야하기 때문에 의미가 퇴색 된다고 생각했다.
2. 위상정렬을 통해서 cycle이 발생하는지 확인 하기
정방향
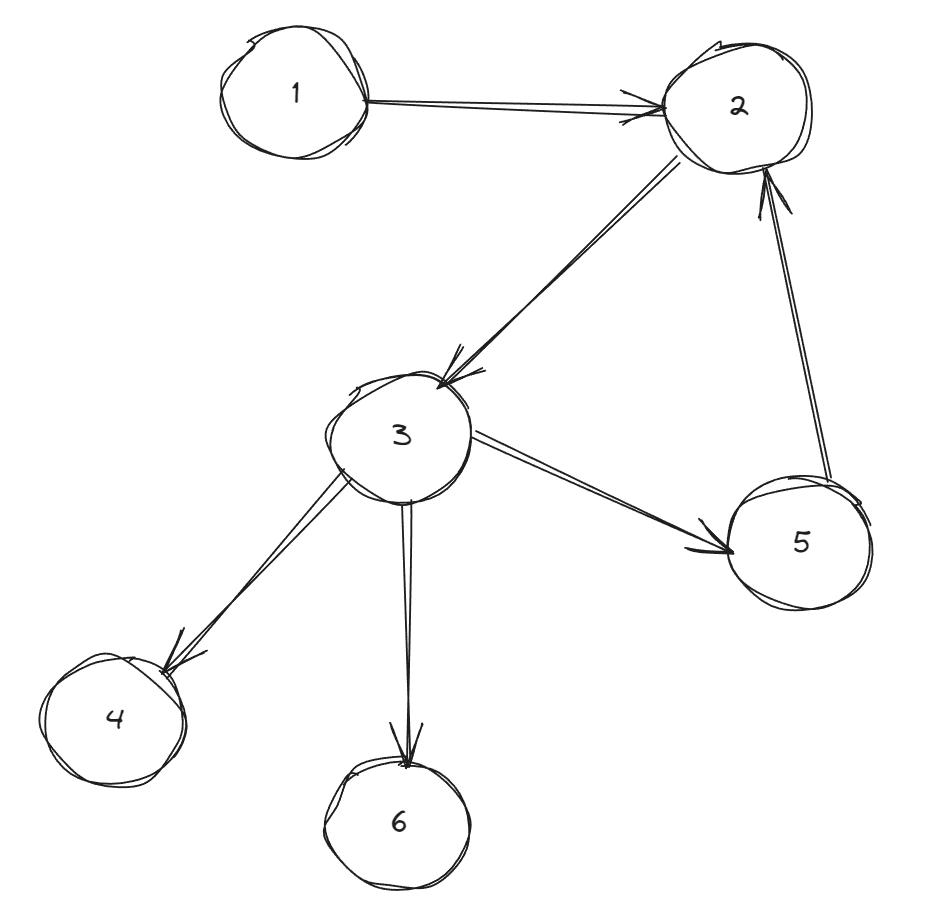
위 그림처럼 그래프가 구현된다고 생각 해보자.
해당 그래프처럼 구현이 된다면 기존 위상정렬 방식으로는 indegree가 0인 1부터 Queue에 삽입 될 것이다.
Queue의 data를 poll하면서 로직을 이어 간다면 cycle이 있는지 여부는 확인 할 수 있을 것이다.
for (int next : relation[cur]){
inDegree[next]--;
if (inDegree[next] == 0){
q.offer(next);
ans++;
}
}선행 되어야 할 정점과 연결되어 있는 모든 정점을 탐색하기에
cycle에 속하지 않는 4, 6 역시 cycle을 판단할때 포함되어서 같이 진행 되므로 따로 분류하기가 껄끄러웠다.
cycle에 포함되지 않는 정점들은 로직에서 완전히 분리하고 싶었다.
역방향
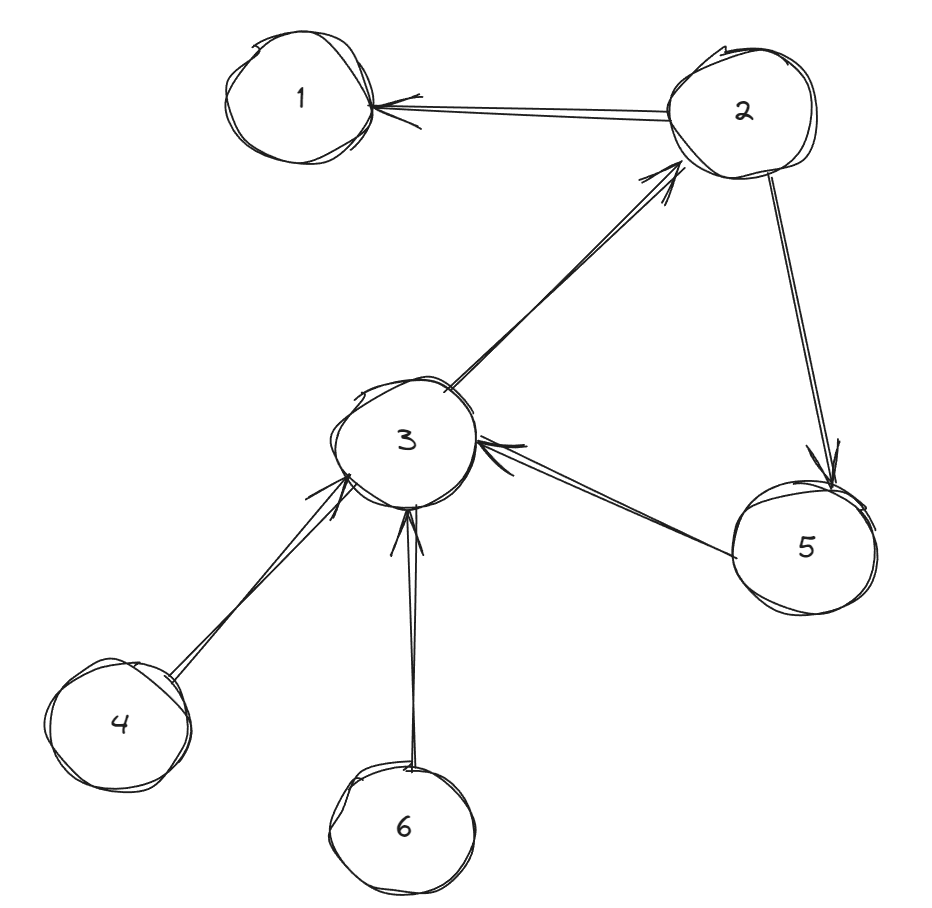
그래프의 간선을 역으로 뒤집는다면 indegree가 0인 차수는 1이 아닌 4, 6으로 시작 한다.
indegree가 0인 4, 6을 Queue에 삽입하고 진행을 하면 이후 어떤 정점도 indegree가 0이 되지 못한다.
indegree가 0이되는 노드들은 cycle에 포함되지 않는 정점이 다.
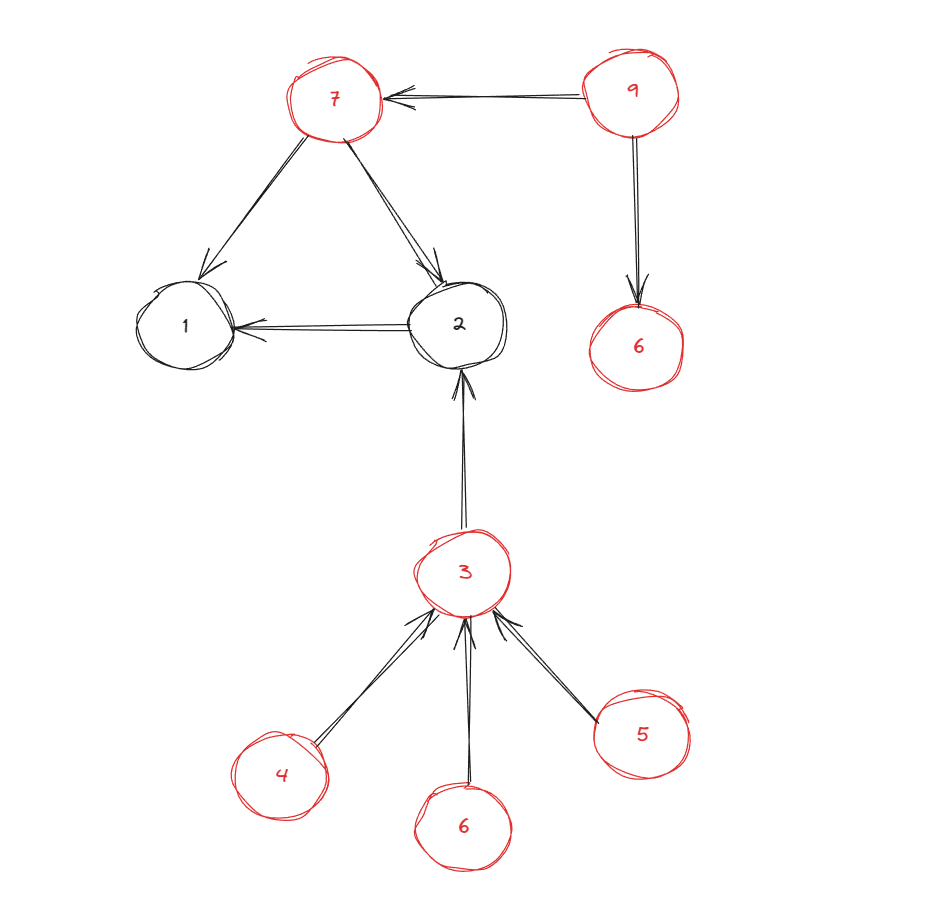
하나의 예시로는 이해가 힘드니 하나 더 생각 해보자.
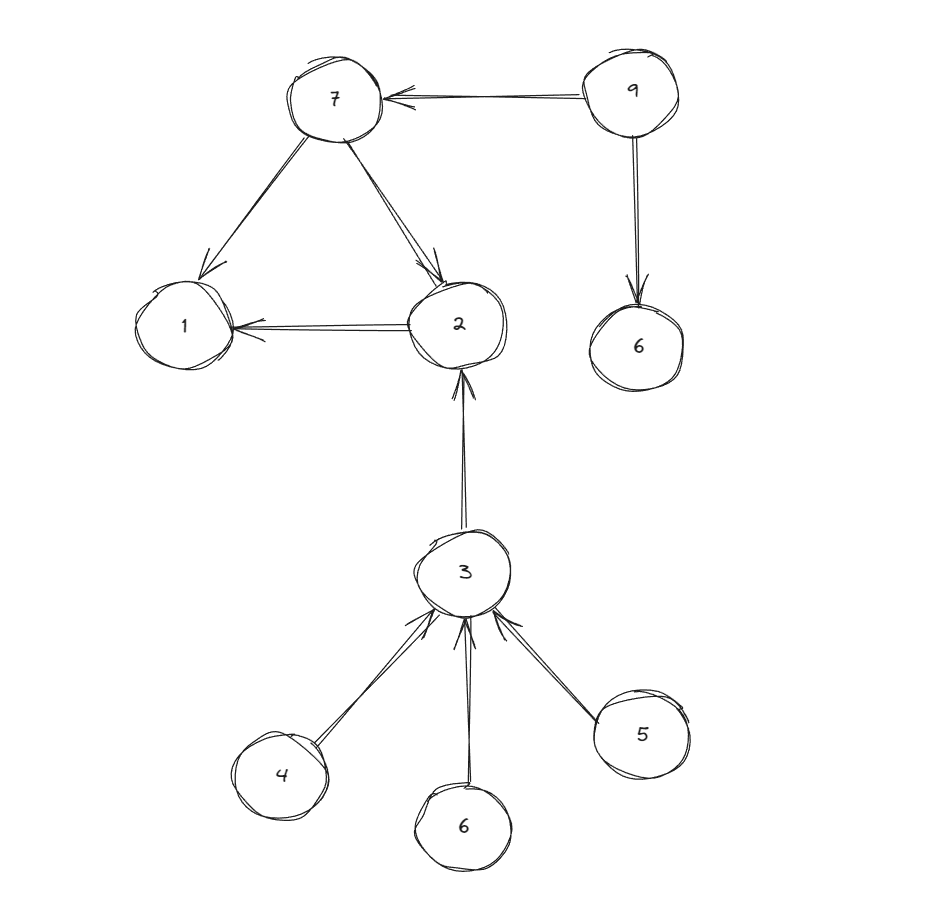
그래프는 이미 간선이 뒤집힌 경우라고 가정한다.
indegree가 0인 정점은 4, 5, 6, 9이다.
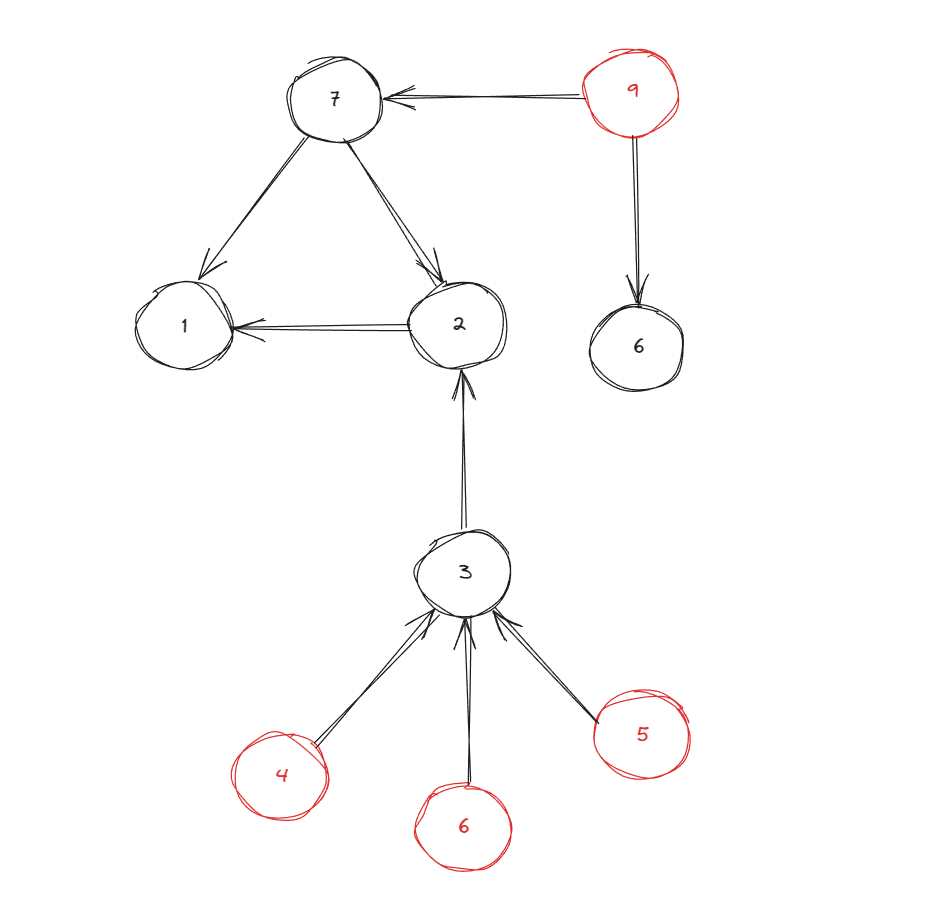
indegree가 0인 정점을 위상정렬을 통해 탐색할때 indegree가 0이되는 정점은 3, 6, 7 이다.
3, 6, 7 정점은 Queue에 삽입 될 것이며 다음 정점의 indegree를 줄여 갈 것이다.
위와 같이 연결된 정점을 계속 반복해서 탐색한다면 모든 정점이 탐색되는 것을 알 수 있다.
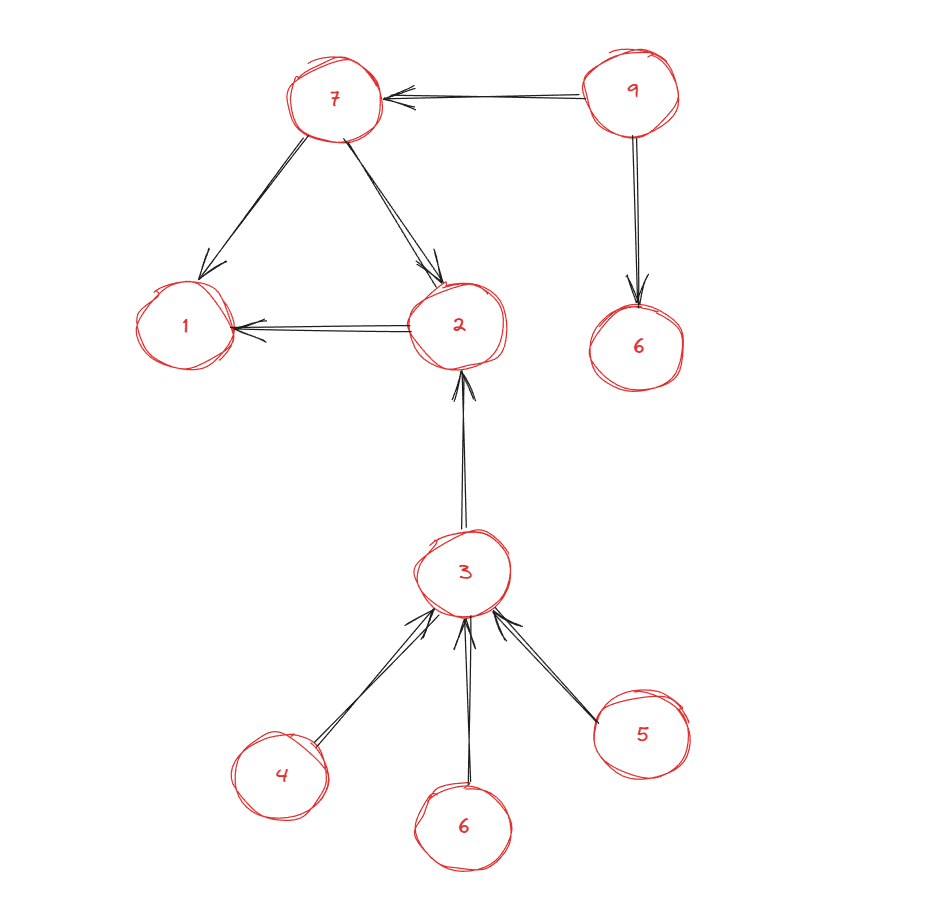
위 예제의 그래프는 모든 정점이 탐색되기 때문에 cycle이 없다고 판단이 가능하다.
💻 제출

📝 제출 코드
import java.io.*;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static ArrayList<Integer>[] relation;
static int[] inDegree;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken()); //부원의 수
M = Integer.parseInt(st.nextToken()); //관계의 수
relation = new ArrayList[N+1];
for (int i=1; i<=N; i++){
relation[i] = new ArrayList<>();
}
inDegree = new int[N+1];
for (int i=1; i<=M; i++){
StringTokenizer stD = new StringTokenizer(br.readLine()," ");
int s = Integer.parseInt(stD.nextToken());
int e = Integer.parseInt(stD.nextToken());
//역방향 연결, 그래프를 뒤집는 로직
relation[e].add(s);
inDegree[s]++;
}
bw.write(topologicalSort() + "\n");
bw.flush();
bw.close();
br.close();
}
static int topologicalSort(){
Queue<Integer> q = new LinkedList<>();
for (int i=1; i<=N; i++){
if (inDegree[i] == 0){
q.offer(i);
}
}
int ans = q.size(); //queue에 삽입된 초기 개수는 cycle에 속하지 않는 정점
while (!q.isEmpty()){
Integer cur = q.peek();
q.poll();
for (int next : relation[cur]){
inDegree[next]--;
if (inDegree[next] == 0){
q.offer(next);
//indegree가 0인 정점은 cycle이 아니다.
ans++;
}
}
}
return ans;
}
}📗 문제를 풀며...
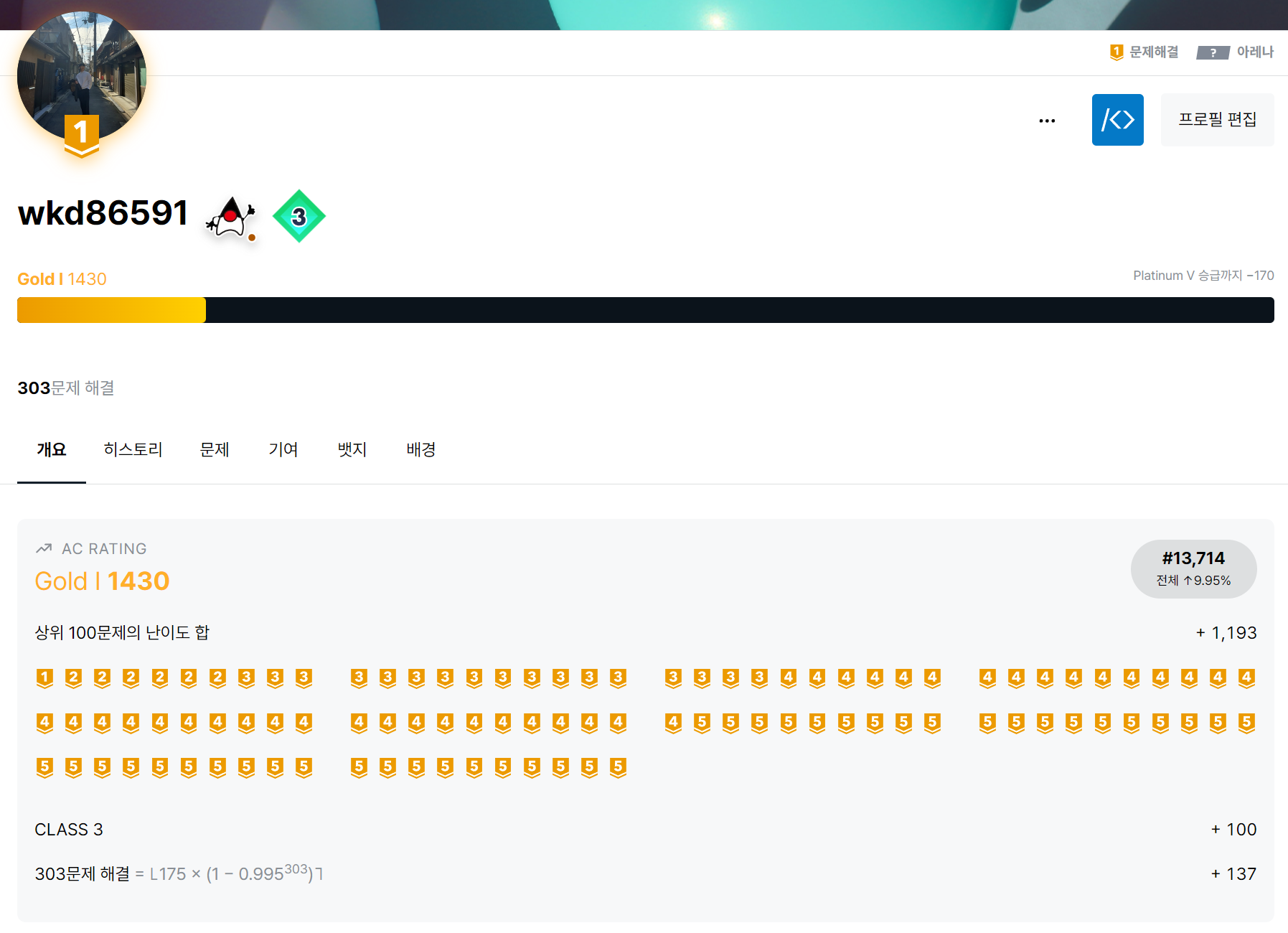
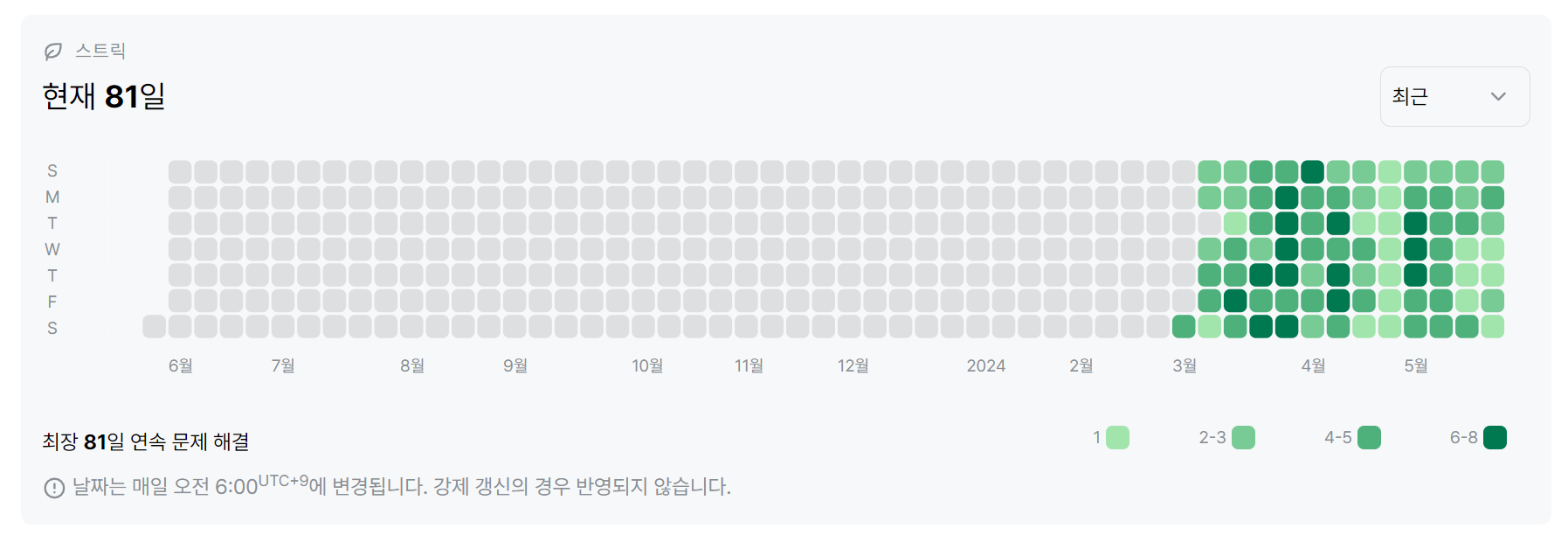
두달 조금 넘는 시간을 백준 문제만 300개 넘게 풀어왔다.
백준 문제를 풀면서 항상 느끼는 불편한 점은 코드를 제출 했을때 체크하는 테스트케이스 반례에 비해 제공되는 반례가 너무나도 적다는 것이다.
물론 완벽한 코드를 제출하기 바랬으면 하는 의도가 있다면 모르겠지만 코딩테스트를 "연습"하는 공간이기에 반례를 넉넉히 문제에 제공해준다면 쓸데없는 삽질을 덜 하지 않을까 하는 개인적인 생각이 있다.
백준에 많은 문제가 있어서 주로 사용하지만 이후 조금 더 숙련도가 쌓인다면 리트코드, 코드포스 등등 다양하게 경험 하는게 효과적일 것 같다.
