백준 2611 - 자동차 경주(Java)

장준혁·2024년 6월 3일

coding test

coding-test

목록 보기

19/21

🔍 문제

📌 입력

📌 출력

💻 제출

🤔 문제 풀이

해당 문제를 풀때 몇 가지의 단서가 존재한다.

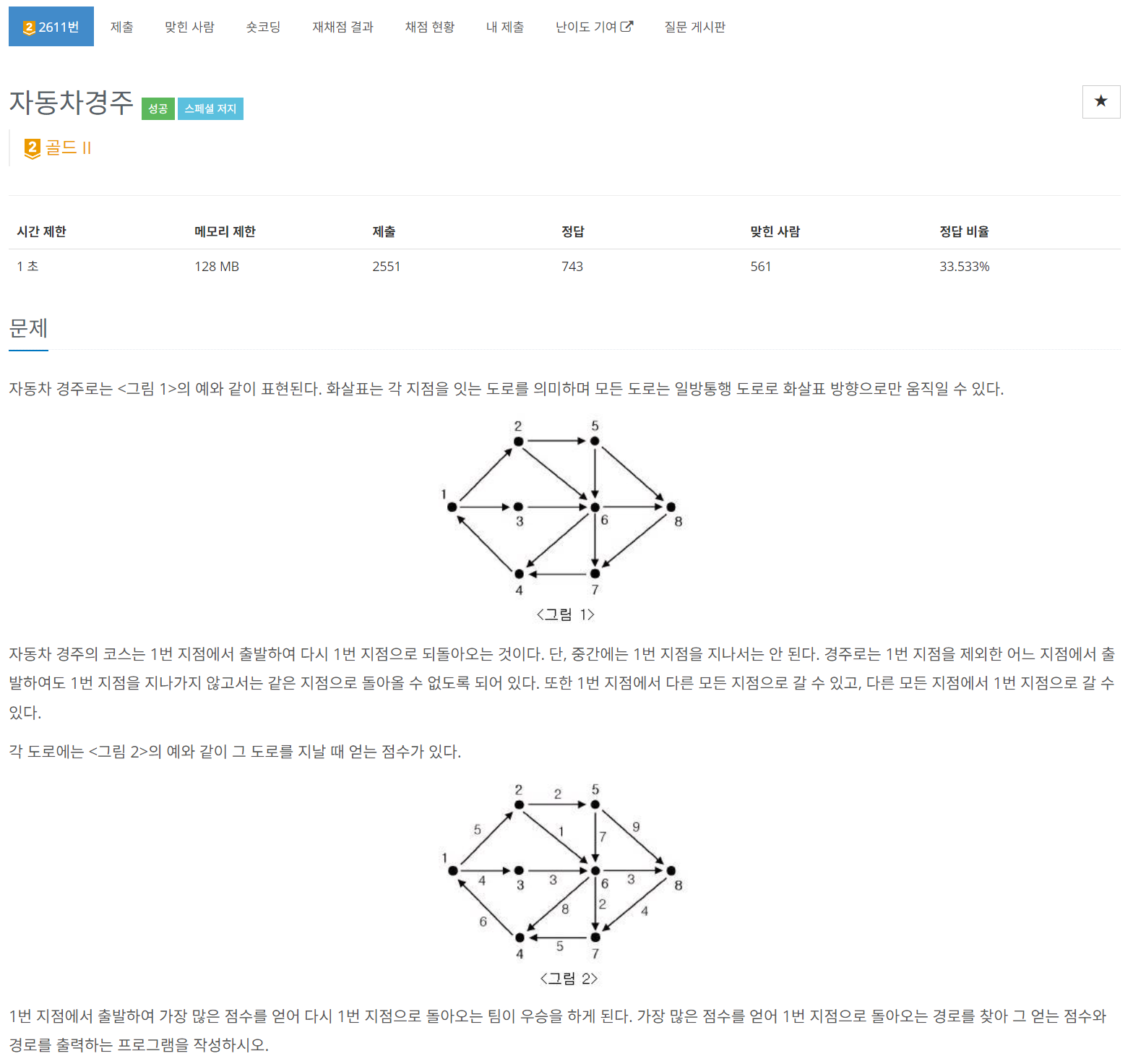
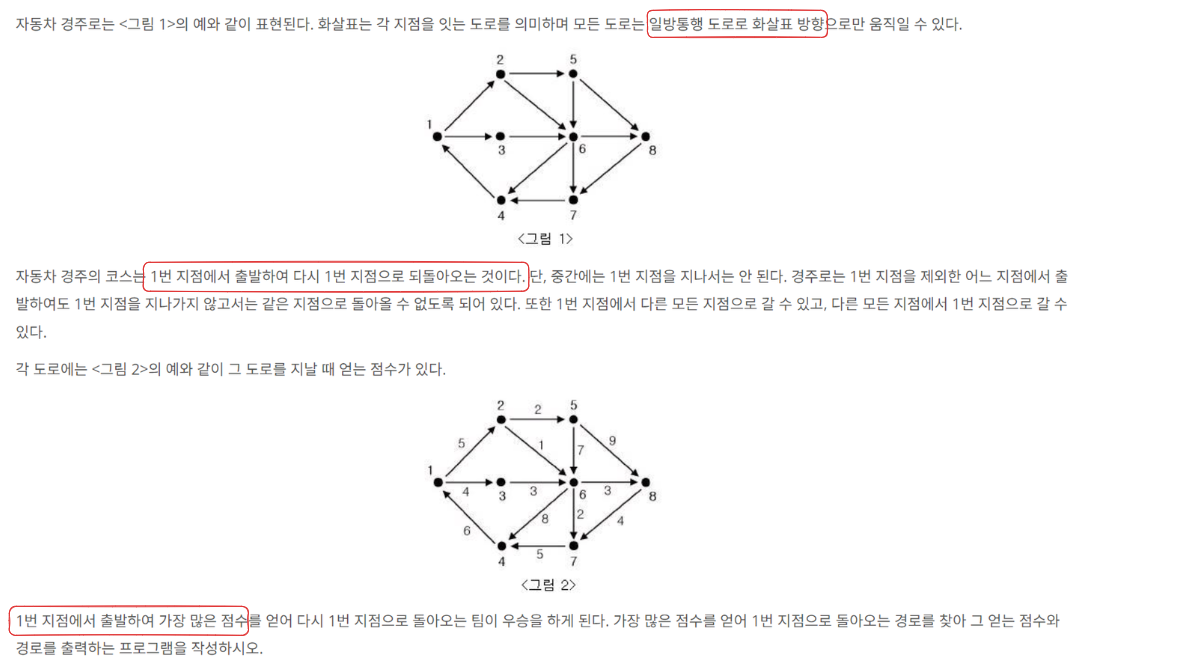
일방통행 도로 라는 말은 방향성이 존재하는 그래프 라는 뜻으로 해석 할 수 있다.
따라서 ArrayList 배열을 통해서 각 정점간의 방향 간선을 입력하기로 했다.
1번 지점에서 시작 하여 1번 지점으로 되돌아 와야 하기 때문에 시작점은 1으로 고정 값이다.
1으로 시작하여 탐색을 진행하고 탐색 도중 다음 정점이 1이라면 cycle이 형성 되는 것 이다.
cycle이 형성되는 최단 경로를 구하는 것이 아닌 최대한 많은 값을 가지는 경로를 구해야 한다.

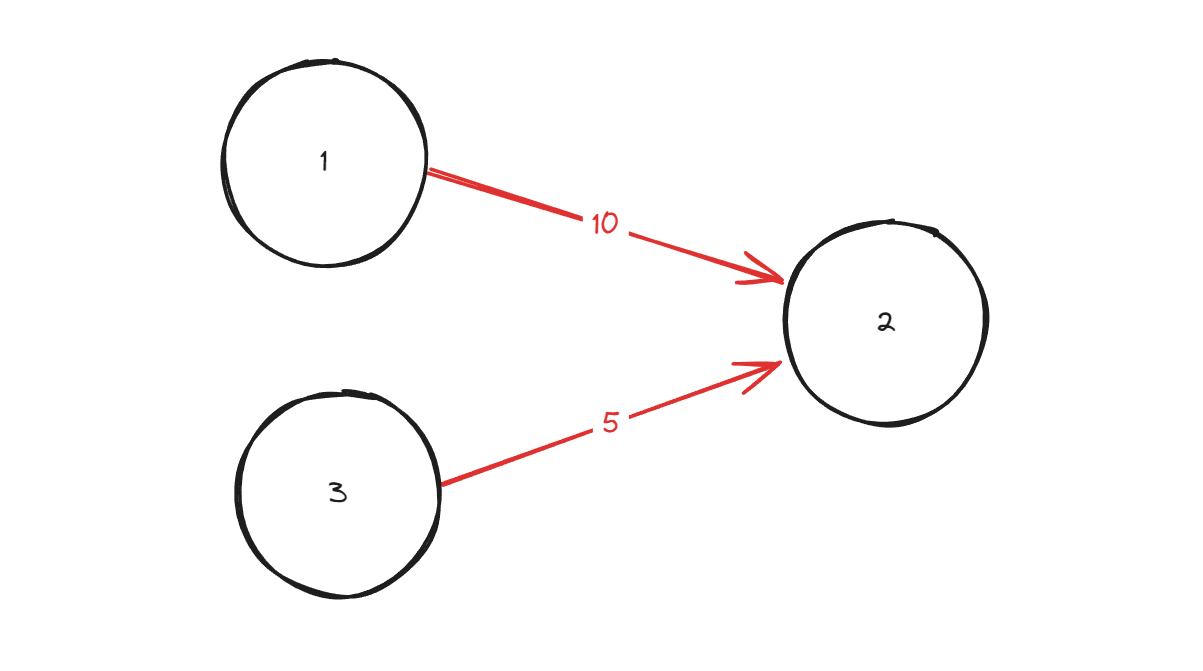
위상 정렬을 사용한다면 2번 정점을 탐색 하기 이전 아래 두 계산이 가능하다.

1번 정점 까지의 가중치 + 1번 에서 2번 까지의 가중치
3번 정점 까지의 가중치 + 3번 에서 2번 까지의 가중치

위 두가지의 값을 비교 해서 큰 가중치 값을 2번 정점에 저장 할 수 있다.

가중치 값을 저장할 때 이전 정점 번호를 저장한다면 역방향 탐색이 가능하다.
(1, 3번 정점의 가중치 값이 동일 하다고 가정 할 때 2번 정점 이전 노드는 3번 정점 이다.)

문제에서 주어진 예제를 통해서 설명 해보겠다.

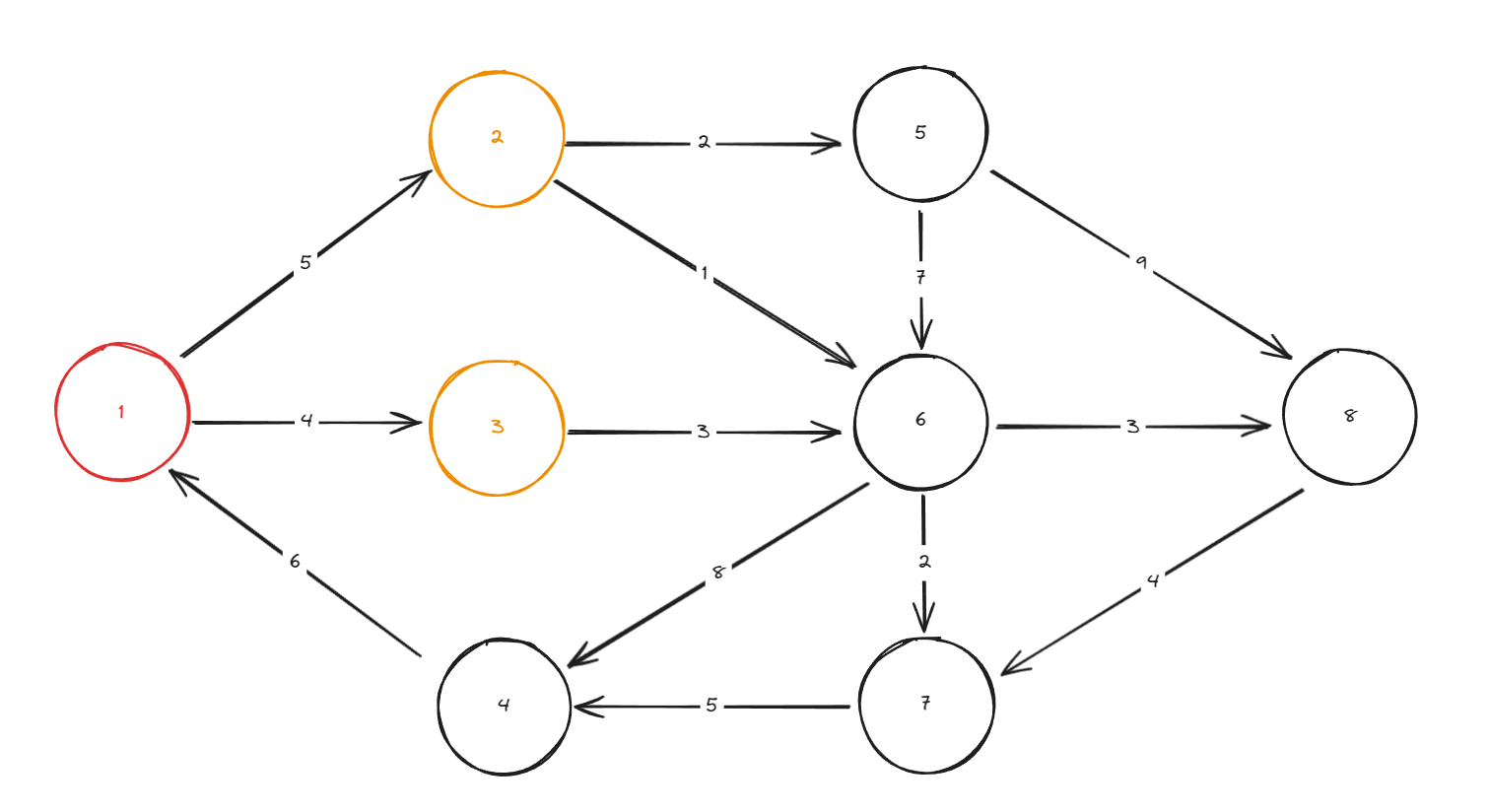
1번 정점을 위상 정렬 탐색 시에 indegree 가 0인 정점은 2와 3이다.

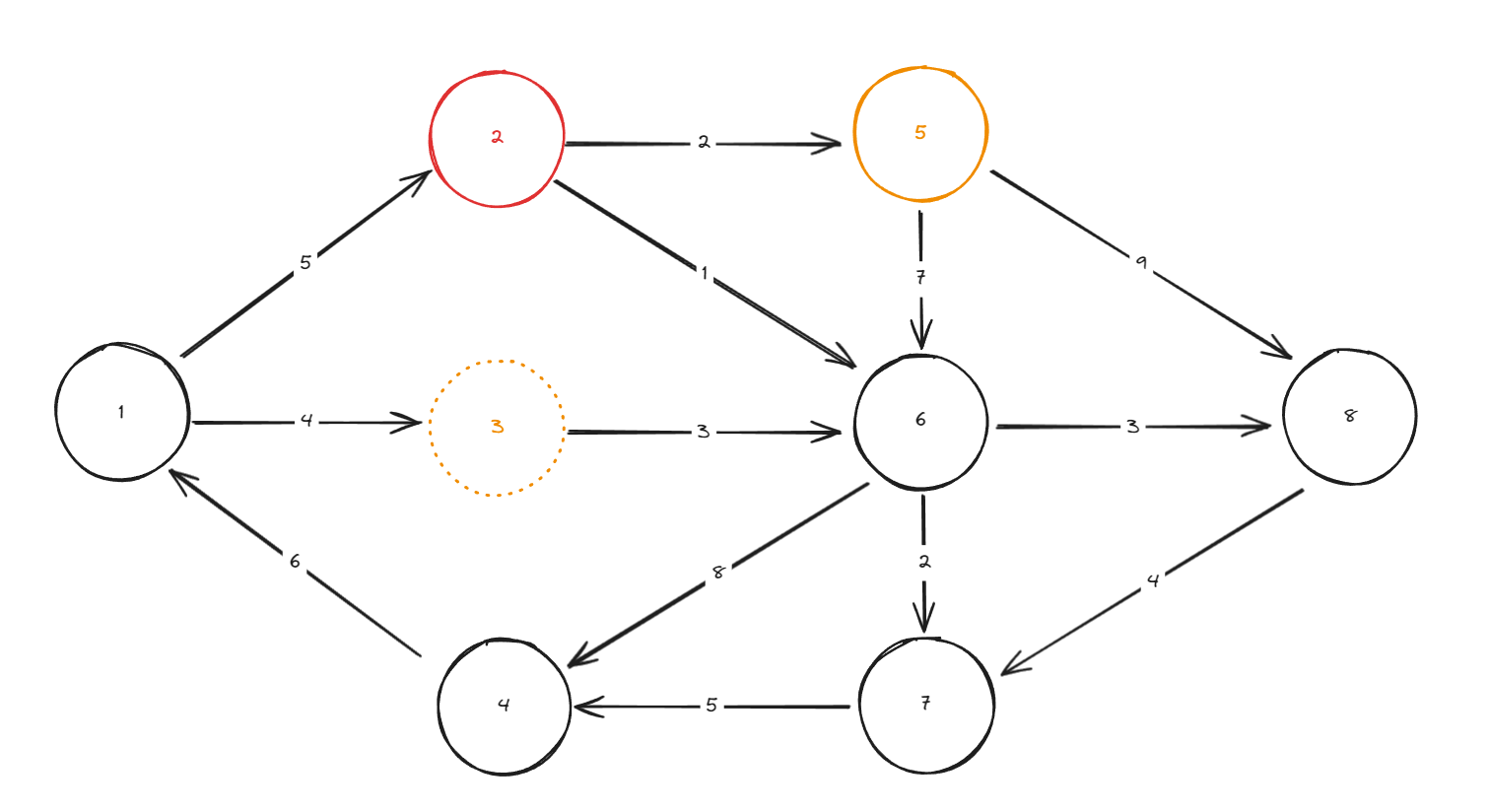
2번 정점을 탐색 시에 5번 정점의 indegree는 0이 되고 6번 정점의 indegree는 1 감소한다.
(3번 정점은 대기 상태)

2번 정점의 이전 정점의 값은 1로 저장 될 것 이다.

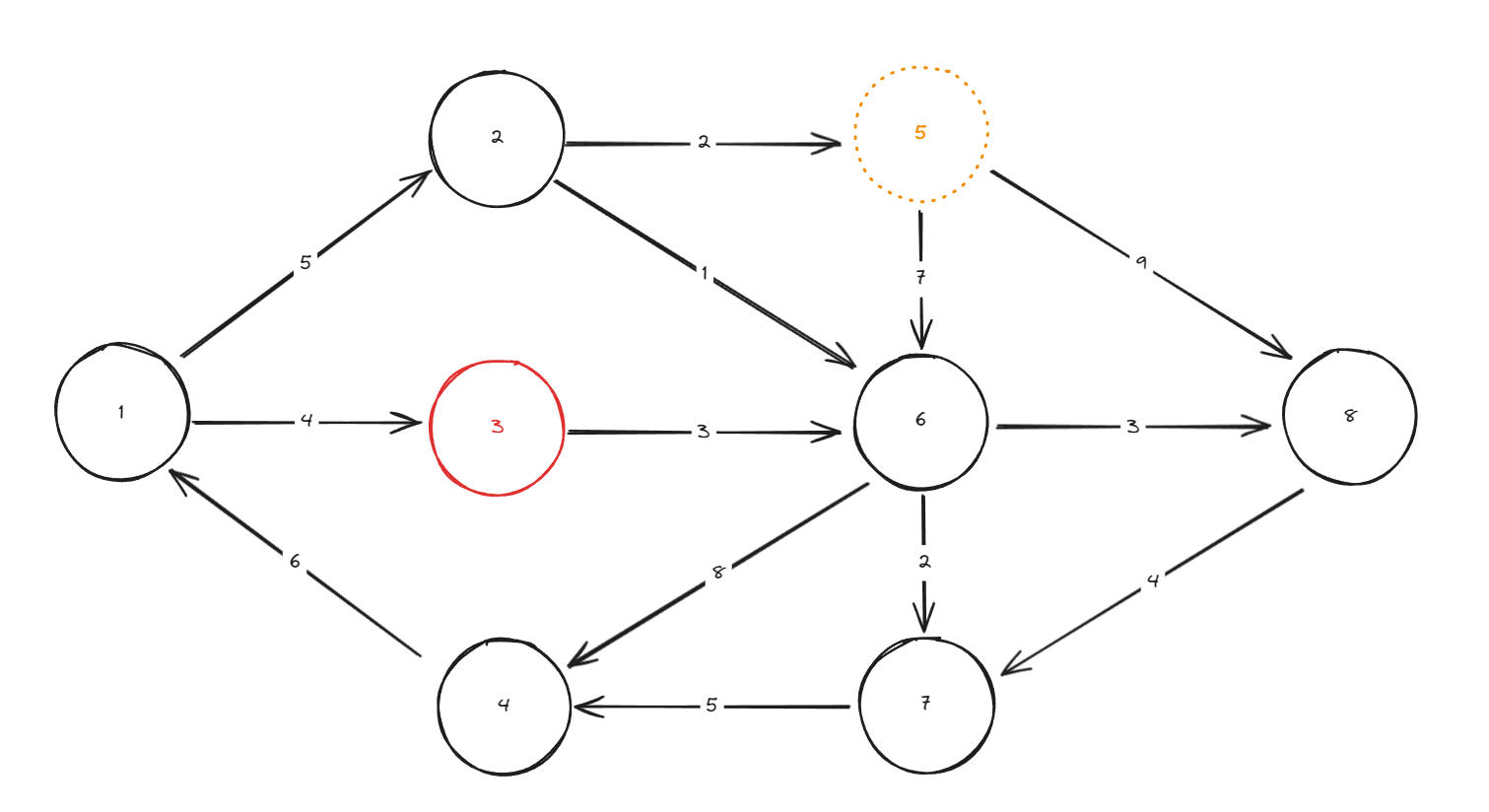
3번 노드 탐색 시 이전 정점의 값은 1이 될 것이다.

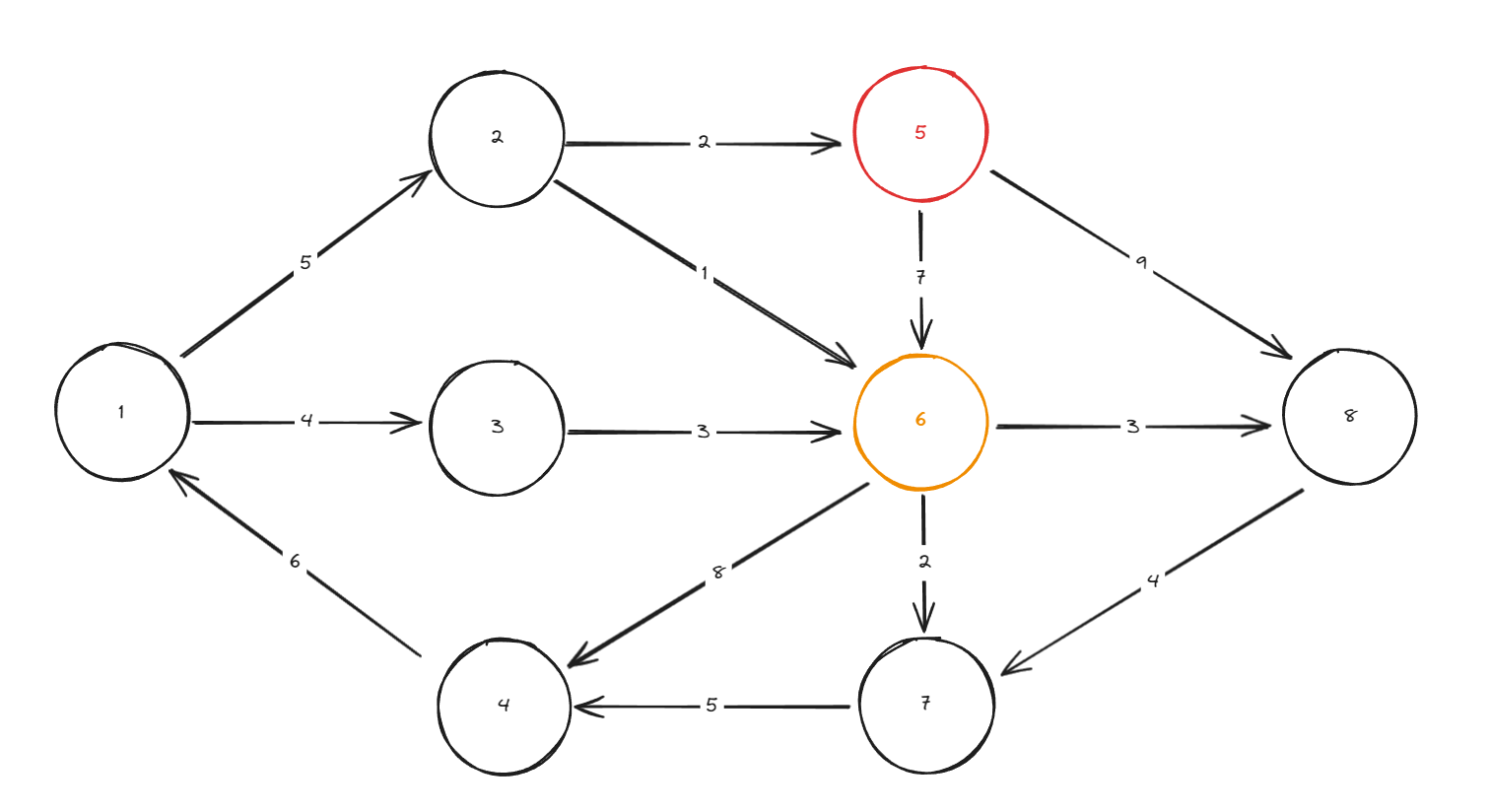
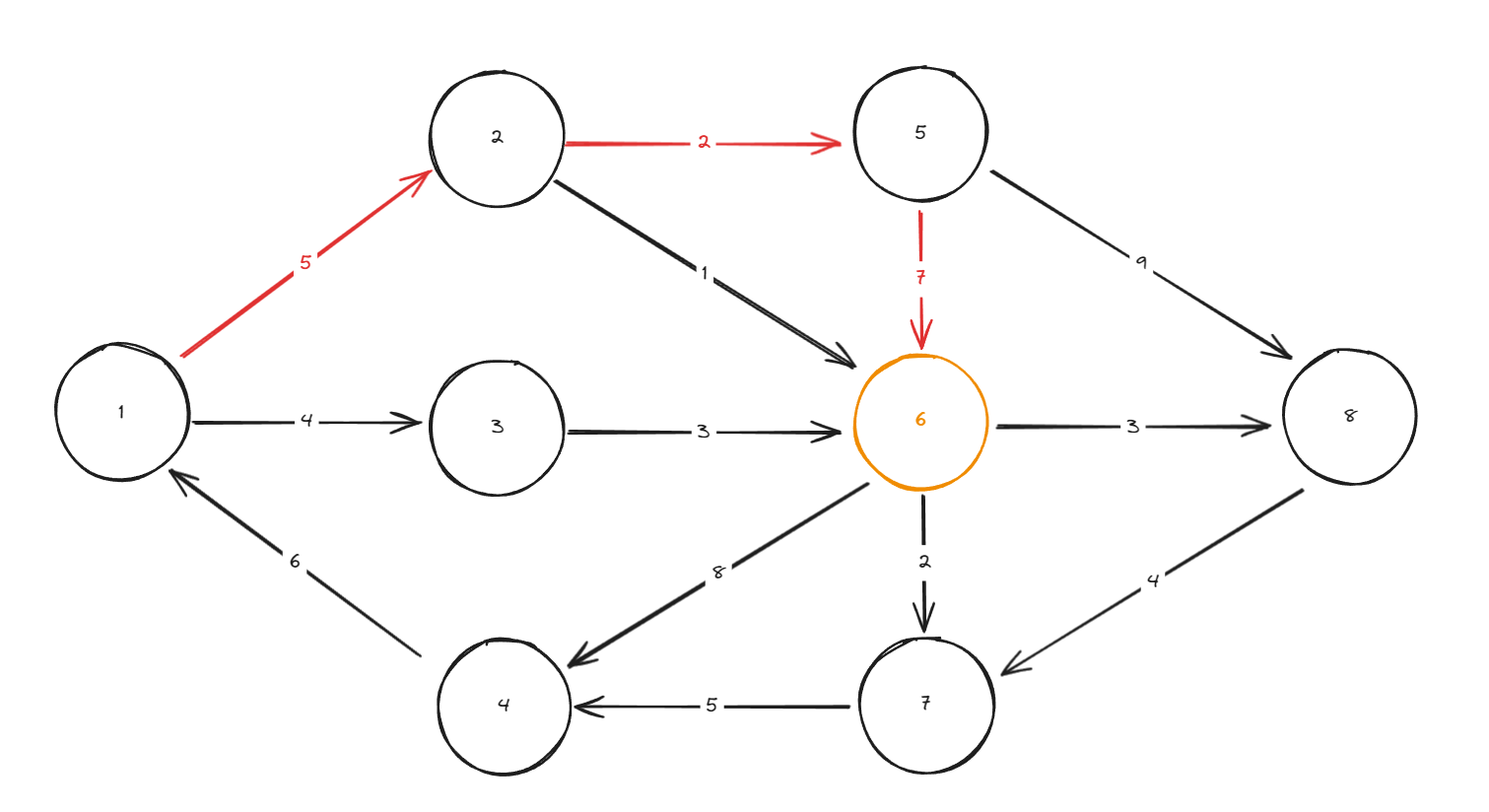
5번 노드 탐색 시에 6번 노드의 indegree가 0이 될 것이며 연결 되어 있는 이전 정점들 중 가장 가중치가 큰 노드는 5번 노드 이다.

위와 과정을 반복 했을 경우

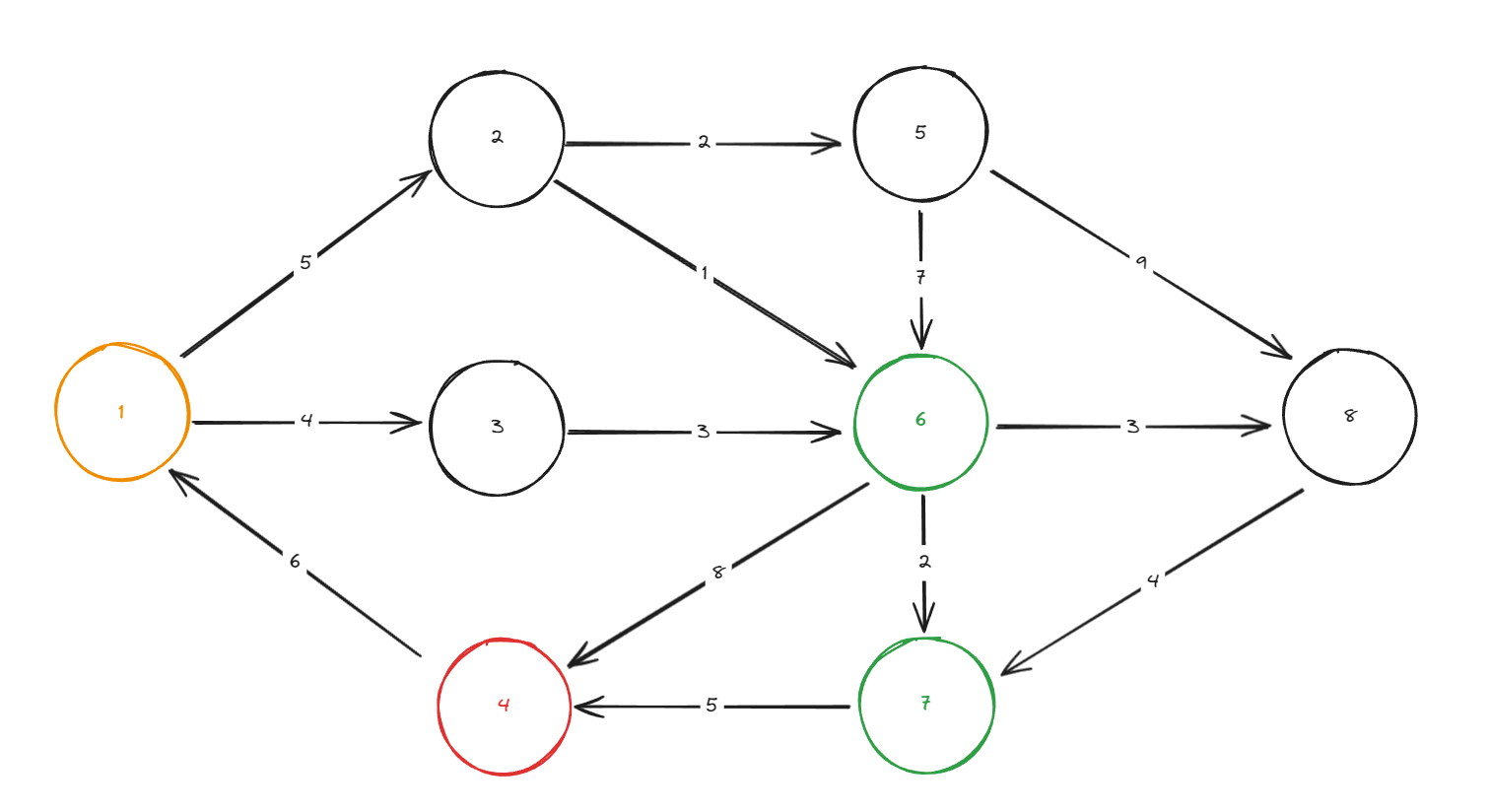
4번 정점의 이전 정점은 6번과 7번 정점 중 가장 가중치가 높은 정점이 저장 될 것이며 4번 정점 탐색 시 다음 indegree가 0인 정점은 1번 정점이다.

1번 정점이 다시 탐색 될 경우 cycle이 형성 된 것이고 1의 이전 정점으로 4번 정점이 저장 된 후 종료 된다.

로직이 종료 된다면 1번 부터 역순으로 이전 정점을 돌아가면서 순서를 저장 한 후 뒤집어 준다.

📝 제출 코드


import java.io.*;
import java.util.*;


public class Main {
    static int N, M;
    static ArrayList<Node>[] graph;
    static int[] inDegree, score, prev;
    static Deque<Integer> dq = new ArrayDeque<>();
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

    static class Node {
        int num;
        int cost;

        public Node(int num, int cost) {
            this.num = num;
            this.cost = cost;
        }
    }

    public static void main(String[] args) throws IOException {


        N = Integer.parseInt(br.readLine()); //정점 수
        M = Integer.parseInt(br.readLine()); //간선 수

        graph = new ArrayList[N + 1];

        for (int i = 1; i <= N; i++) {
            graph[i] = new ArrayList<>();
        }

        inDegree = new int[N + 1];

        for (int i = 0; i < M; i++) {
            StringTokenizer stD = new StringTokenizer(br.readLine(), " ");

            int s = Integer.parseInt(stD.nextToken());
            int e = Integer.parseInt(stD.nextToken());
            int v = Integer.parseInt(stD.nextToken());

            graph[s].add(new Node(e, v));
            inDegree[e]++;
        }

        solved();

        bw.write(print() + "\n");

        bw.flush();
        bw.close();
    }

    static void solved(){
        score = new int[N + 1];
        prev = new int[N + 1];

        dq.offerLast(1); // 시작 정점 = 1

        while (!dq.isEmpty()){
            Integer now = dq.pollFirst();

            for (Node next : graph[now]){
                int nextCost = score[now] + next.cost;

                if (score[next.num] < nextCost){
                    score[next.num] = nextCost;
                    prev[next.num] = now;
                }

                inDegree[next.num]--;

                if (inDegree[next.num] == 0 && (next.num != 1)){
                    dq.offerLast(next.num);
                }
            }
        }
    }

    static String print() throws IOException{
        bw.write(score[1] + "\n");

        StringBuilder sb = new StringBuilder();

        int num = 1;
        while (true){
            if (prev[num] == 1){
                dq.offerLast(1);
                break;
            }

            dq.offerLast(prev[num]);
            num = prev[num];
        }

        while (!dq.isEmpty()){
            sb.append(dq.pollLast()).append(' ');
        }

        sb.append("1 ");

        return sb.toString();
    }

}