해시테이블 -1-

---

해시테이블이란?

• 해시함수를 적용한 key / value 자료구조
• hash 함수로 변환한 값을 index로 value를 찾는다.

---

1.Direct Address Table :
키 값을 index로 사용 하여 테이블에 접근

• 장점
  - 탐색 삽입 삭제 연산이 O(1)
• 단점
  - 최대 키 값을 알고 있어야 함(max key값의 인덱스 크기를 가지는 배열)
  - 최대 키 값이 클 때는 메모리 낭비가 심함.
  - 키 값이 골고루 분포 되지 않을 경우 메모리 낭비가 심함.

2. Hash Table:
키 값에 해시 함수를 적용하여 인덱스 값을 알아낸 후, 해당 인덱스에 value를 저장. 해시함수의 특성 상 충돌(collision)이 발생 하고, 이 충돌에 대한 처리가 필수적이다.

---

충돌이란?

충돌의 개념을 이해하기 위해선 먼저 비둘기집 원리를 이해해야 한다. 비둘기가 n+1 마리가 있다고 가정하자. 그리고 비둘기 집이 n개 있고, 각 비둘기 집에는 비둘기가 단 한 마리 들어갈 수 있다고 가정하자. 그렇다면 비둘기 집에 들어가지 못 한 비둘기가 최소 한 마리 이상 존재한다.

이제 이걸 함수 관점에서 생각해보자. 비둘기 집합은 정의역(Domain)이 되고, 비둘기 집은 치역(range)가 된다. 해시 함수도 함수이므로, 정의역과 치역이 존재한다. 해시 함수의 정의역은 임의의 길이 l의 데이터 집합, 그리고 해시 함수의 치역은 정해진 길이 L의 데이터 집합이다.

그렇다면 max(l) > L인 경우, 비둘기집 원리로 인해 정의역에 속하는 일부 데이터들은 중복으로 치역에 매핑 되게 된다. 이렇게 해시 함수의 정의역이 치역(테이블 크기)에 비해 얼마나 큰 지에 대한 성질을 적재율(Load Factor)을 통해 표현할 수 있다. 적재율은 비둘기 / 비둘기집 비율이라고 생각하면 된다.

적재율(Load Factor) : K=key의 수(비둘기의 수),N=테이블의 크기(비둘기집의 수)
$Load Factor = K/N$

그리고 load facor > 1인 경우 반드시 충돌이 발생하게 된다. 비둘기가 더 많은 것이다.

---

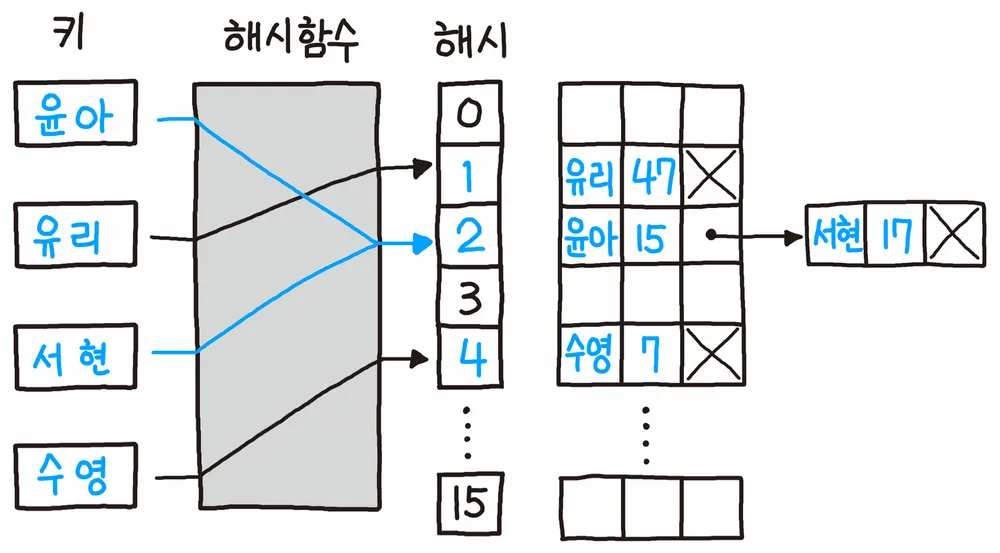
해시 충돌(Collision) 발생시 처리 방법

1. chaining : 말 그대로 충돌이 발생한 인덱스를 동일한 버켓에서 링크드 리스트로 이어 놓는 방법이다. 입력한 키 값에 모두 충돌이 발생한 최악의 경우 O(K) 탐색 시간이 걸린다.

이미지 출처

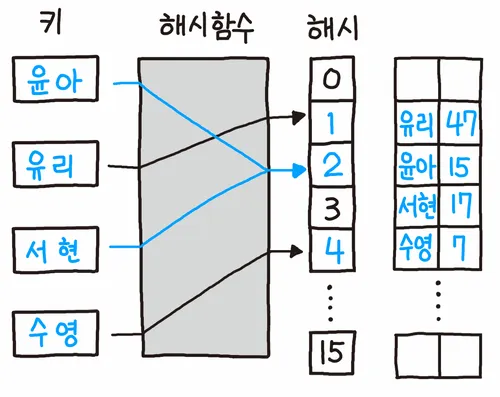
2. Open addressing : 충돌 발생 후 비어 있는 다른 버켓을 탐색 후 삽입하는 방법이다. 비어 있는 버켓을 찾는 탐사 방법은 선형 탐사, 제곱 탐사, 이중 해싱 등이 있다.

이미지 출처

chaining이 충돌이 발생한 버킷 바로 그 위치에서 링크드리스트로 삽입을 하여 해결하는 방법이라면, open addressing은 충돌이 발생한 위치에 삽입을 하지 않고 탐색(probing) 알고리즘을 추가해서 비어 있는 버킷에 데이터를 삽입 하는 방법이라고 생각하면 된다. 즉, 충돌 지점에서 충돌 문제를 해결하느냐, 충돌 지점이 아닌 다른 곳에 데이터를 삽입해서 문제를 해결하느냐 방법의 차이다.

---

해시 함수 개선

위의 방법들은 충돌 발생 후, 즉 해시충돌에 대한 사후 처리에 대한 방법론이었다. 하지만 이 외에도 해시함수 자체를 사전적으로 개선하는 방식으로 해시충돌을 개선할 수 있다.

1. 나눗셈법(Division Method): 입력값 % 테이블의 크기로 인덱스를 구하는 방법이다.

   $hash(k) =\;k\;mod\;N$

   여기서 테이블의 크기는 N이고 입력 키 값은 K가 되는데, 테이블 N의 값은 소수를 쓰게 된다. 왜 그럴까? 소수는 1과 자기 자신으로만 나누어지게 된다. 즉, 해시 충돌은 소수를 사용할 경우 균일할게 분포되어 발생한다. 아래의 경우 자연수 m의 배수 단위로 같은 해시값이 리턴된다.

   $k\;mod\;(p*m) =\;k\;mod(p)$

2. 곱셈법 : $0<A<1$인 A에 대하여 아래의 해시함수를 정의할 수 있다.나눗셈 법보단는 느리고 2진수 연산에 최적화된 컴퓨터 구조를 고려한 해시 함수라는데, 정확하게 이해 후 내용을 추가해야 할 것 같다.

   $hash(k) = N(kA\;mod\;1)$

3. 자릿수 접기(Digits Folding):
   각 자릿수를 전부 더해 해시 값을 만든다. 예를 들어 92321를 자릿수 접기를 하면 9+2+3+2+1 = 17로 5자리 숫자가 2자리 숫자로 해싱 된다. 문자열 또한 자릿수 접기를 할 수 있는데, 각 문자는 아스키 코드 (정수)에 대응 되므로, 각 문자를 더해 얻은 수가 자릿수 접기로 해싱된 해시값이다. HELLO = {72,101,,108,108,111} $\rightarrow$ 72+101+108+108+111 = 500 HELLO를 폴딩해서 500이라는 해시값을 얻을 수 있다.