빠른 정렬

빠른 정렬(Quick Sort)

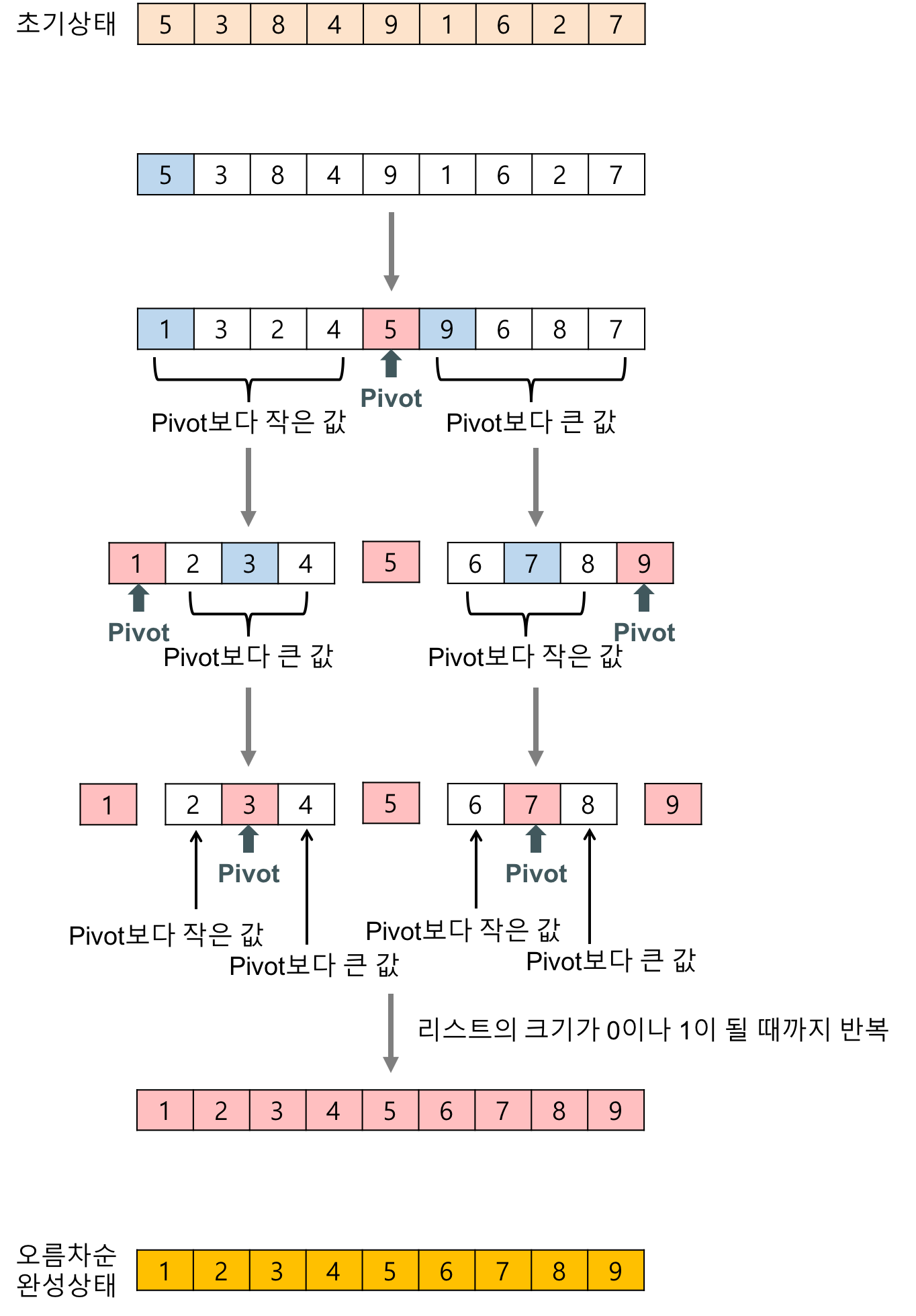
• 기준점을 획득한 다음 해당 기준점을 기준으로 배열을 나눔
• 한쪽에는 기준점보다 큰 항목들이 위치하고 다른 쪽에는 기준점보다 작은 항목들이 위치함.
• 이런 식으로 모든 항목이 정렬될 때까지 이 과정을 반복함
• 가장 이상적인 기준점은 배열의 중간값.
• 중간 값이 배열을 균등하게 나눌 수 있기 때문
• 하지만 정렬되지 않은 배열의 중간값을 얻기 위해선 계산하는 데 선형 시간이 걸림. 따라서 일반적으로 분할 부분의 첫 번째 항목과 중간 항목, 마지막 항목의 중간 값을 취해 기준점얻음
• 이러한 정렬은 재귀 정렬이고 분할 정복 방식을 사용해 시간 복잡도를 이차에서 O(nlog2(N))으로 낮춤.
• 하지만 모든 항목을 한쪽으로만 위치시키는 기준점을 선택하는 최악의 경우 시간 복잡도는 O(N^2)
• 시간복잡도: 평균은 O(nlog2(N)), 최악은 O(N^2)
• 공간복잡도: O(log2(N))
• 단점
  • 기준점을 항상 잘못 선택한 경우는 시간복잡도가 최악으로 나올수 있음.
  • 잘못된 기준점은 배열을 균등하게 분할하지 않음
  • 이상적인 기준점은 배열의 중간 항목
  • 다른 알고리즘과 비교할 대 더 큰 공간복잡도가 필요(재귀 때문)
• 평균 성능이 최적화돼야 하는 경우에 빠른 정렬 알고리즘
• 램 캐시에 대해 더 나은 성능을 보임

코드 구현

const quickSort = items => {
  return quickSortHelper(items, 0, items.length-1)
}

const partition = (arr, left, right) => {
  let pivot = arr[Math.floor((right+left)/2)];
  
  while(left <= right) {
  	while(pivot > arr[left]) {
      left++;
    }
    while(pivot < arr[rigth]) {
      right--;
    }
    
    if(left<=right) {
      [arr[left], arr[right]] = [arr[right],arr[left]];
      left++;
      right--;
    }  
  }
  return left;
}

const quickSortHelper = (items, left, right) => {
  let idx;
  
  if(items.length > 1) {
    idx = partition(items, left, right);
    
    if(left < idx - 1) {
      quickSortHelper(items, left, idx-1);
    }
    
    if(idx < right) {
      quickSortHelper(items, idx, right);
    }
  }
  return items;
}
quickSort([6,1,23,4,2,3]); // [1,2,3,4,5,6,23]