심볼 기반 함수의 점근적 바운드

1. 심볼 기반 함수의 점근적 바운드

• 알고리즘의 복잡도가 점근적으로 n이 크게 증가했을 때 어떻게 행동하는지 표현할 수 있는 여러 가지 노테이션들이 있다.

2. 세타, 빅오, 빅오메가 노테이션

• 세타 노테이션은 알고리즘의 정확한 복잡도를 의미.
  • f(n) = θ(g(n))
  • 0 <= c₁g(n) <= f(n) <= c₂g(n)
  • 위의 경우 f(n)을 θg(n)이라고 함.
  • n > n₀일 때
    
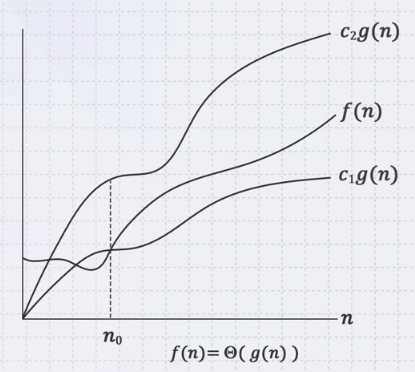
  • f(n)은 g(n)과 같은 속도의 증가속도를 가진다.
  • f(n)은 θg(n)에 속한다.
  • g(n)은 f(n)의 점근적으로 타이트하게 바운드하고 있다.
  • f(n) = θ(nᵏ)
    • ½n²-3n = θ(n²)
    • ⅛n² <= ½n²-3n <= n²
    • 단, n>3
• 빅오 노테이션은 알고리즘의 상한을 의미.
  • 세타 노테이션의 위쪽만을 취하고 아래쪽은 제외한 노테이션
  • 최악의 경우를 표현하기 좋다.
  • f(n) = O(g(n))
  • 0 < f(n) < cg(n)
  • n > n₀
    
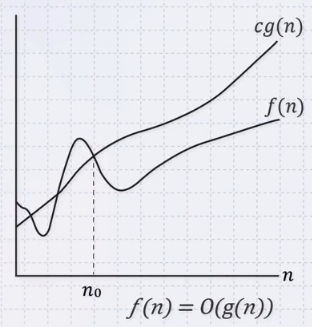
  • 이 때, g(n)은 f(n)보다 위에 있는 바운드라고 해서 upper bound라고 함.
  • f(n) = θ(g(n))이면 f(n) = O(g(n))
  • 빅오 노테이션은 위에 upper bound를 덮어주는 것이 때문에
    f(n)은 절대 cg(n)을 넘어가지 않으므로, 알고리즘의 worst case 러닝타임을 애기할 때 유용하게 사용할 수 있음.
  • 2n²+8n-2 = O(n²) -> ok
  • 2n²+8n-2 = O(n³) -> ok
  • 2n²+8n-2 = O(n⁴) -> ok
  • 2n²+8n-2 = O(n) -> x
    • n은 2n²의 위로 갈수 없기 때문
• 빅오메가 노테이션은 알고리즘의 하한을 의미.
  • 세타 노테이션의 아래쪽만을 취하고 위쪽은 제외한 노테이션
  • asymptoticaly lower bound
  • 이 노테이션은 아무리 빨라도 이것보다 느리다고 애기할 때 사용됨(best case running time)
    
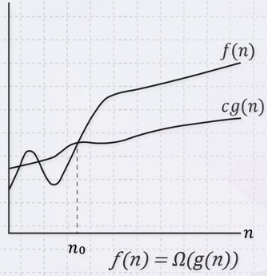
  • f(n) = θ(g(n)) = Ω(g(n))
  • f(n) = θ(g(n)) if and only if f(n) = O(g(n)) and
    f(n) = Ω(g(n))

리틀 노테이션

• 리틀 오, 리틀 오메가의 경우 빅오, 빅 오메가 노테이션과 달리
  점근적으로 타이트한 바운더리를 의미함.

tip

• if and only if: 필요충분조건. 양쪽이 필요충분관계에 있다.
• 유니코드 문자 백과 사전

참고

• 인공지능을 위한 알고리즘과 자료구조(함수의 점근적 분석법)