[Python] 다항식의 저장 방식 (배열, 리스트)

📌 What to do?

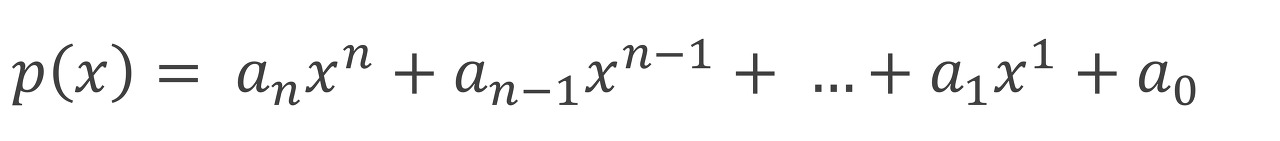
위의 그림은 일반적인 다항식의 형태이다.
위와 같은 다항식을 배열 혹은 리스트에 저장하는 방식은 크게 두가지가 있다.

1) 다항식의 모든 항을 저장하는 방식

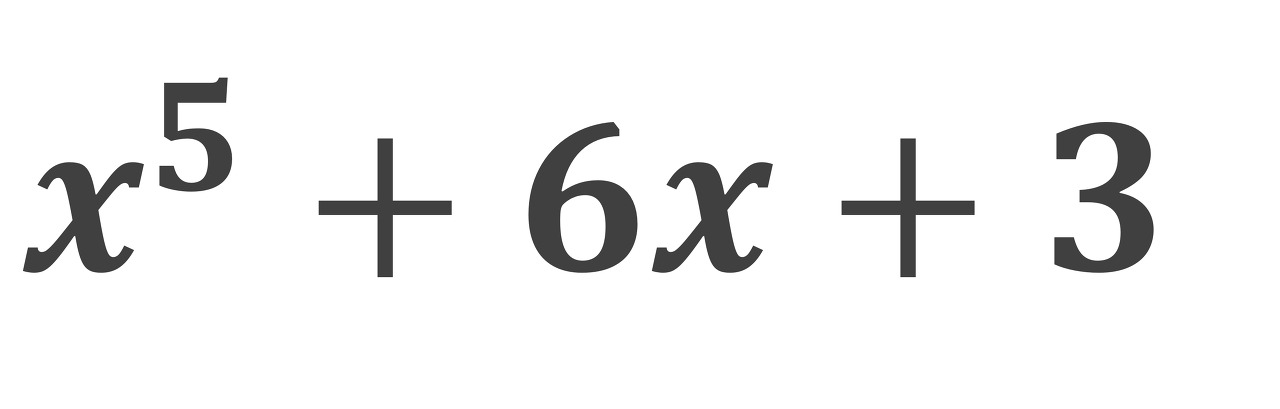
예를 들어 다음과 같은 다항식이 주어졌을때, 이를 1번 방식으로 배열(리스트)에 저장한 형태는 다음과 같다.

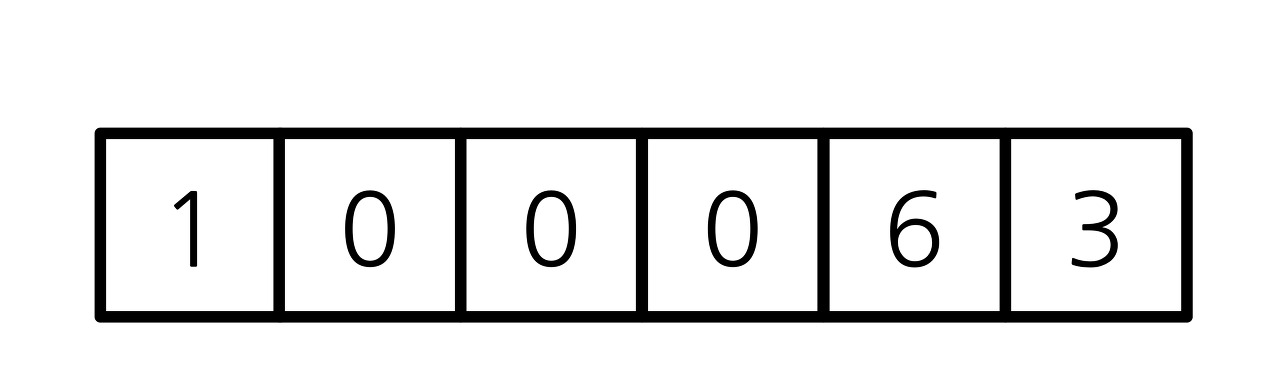
1번 방식의 장단점은 다음과 같다.

• 장점: 다항식의 각종 연산이 간단하다.
• 단점: 항의 계수가 0인 항이 많으면 공간의 낭비가 크다.

2) 다항식 중 계수가 0이 아닌 항만을 저장하는 방식

위의 다항식을 2번 방식으로 배열(리스트)에 저장한 형태는 다음과 같다.

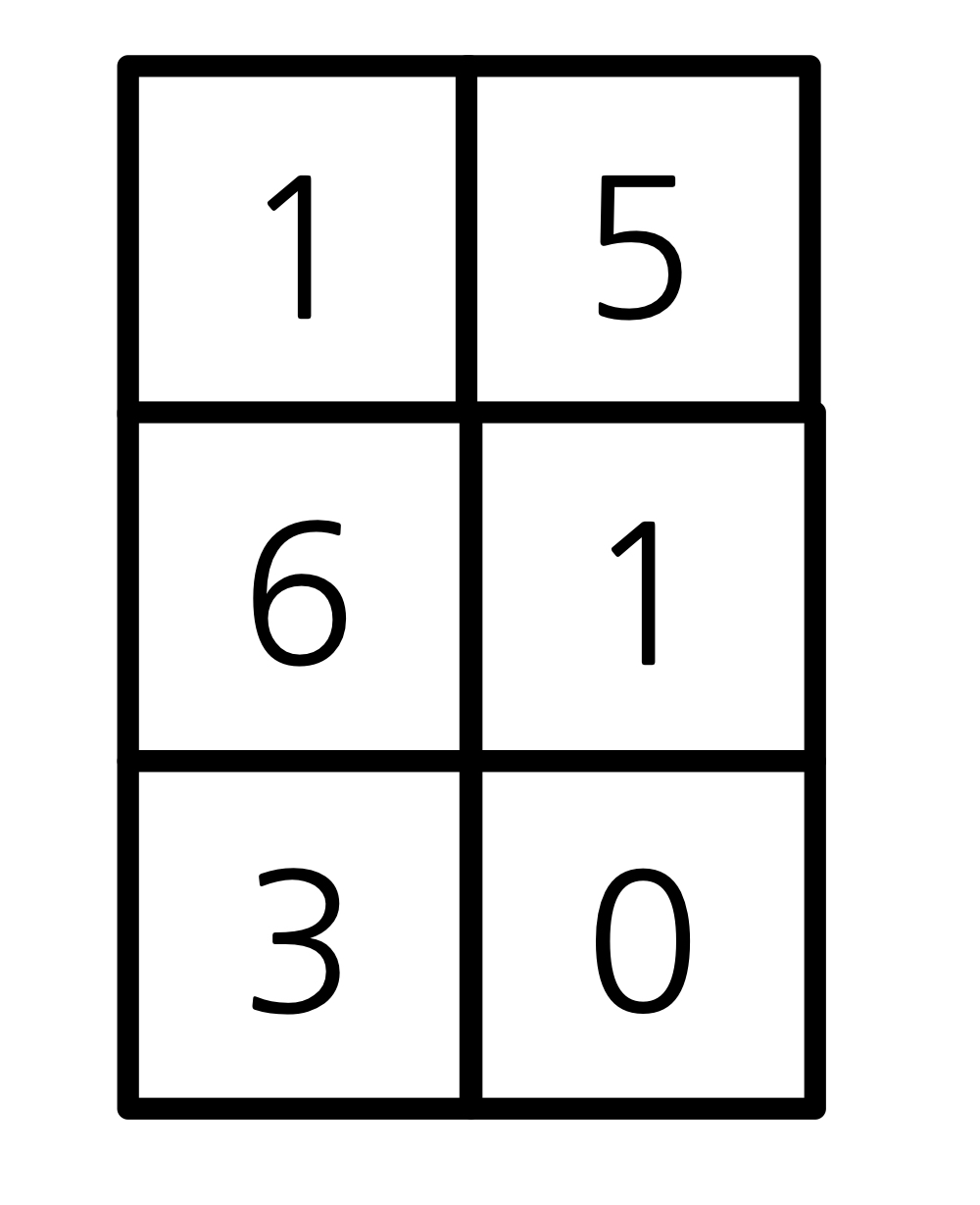
2번 방식의 장단점은 다음과 같다.

• 장점: 메모리 공간을 효율적으로 활용할 수 있다.
• 단점: 다항식의 각종 연산이 복잡하다.

위의 두가지 방식 각각에 대하여 다음과 같은 프로그램을 작성한다.

⚡️ 프로그램의구성

• 입력된 데이터로부터 다항식을 구성하여 화면에 표시한다.
• 입력된 2개의 다항식의 합과 곱을 화면에 표시한다.
• 4개의 다항식 중 하나를 선택하여 𝒙에 값을 대입하면 그에 대한 결과 값을 표시한다.
• 입력되는 다항식의 차수는 최대 5를 넘지않는다.
  
  

1. 다항식의 모든 항을 배열에 저장하는 방식

```python class poly1(): def __init__(self, coef): self.coef = coef self.degree = len(coef) ``` 우선 다항식을 표현하기 위해 **poly1** 클래스를 선언해준다. 이때 **coef**는 다항식의 각 항의 계수를 담아 줄 변수이고, **degree**는 다항식의 최대 차수를 담아 줄 변수이다.

🛠 print_poly1( )

def print_poly1(self):
    for i in range(self.degree):
        if i == self.degree - 1:                        # 상수항인지 판별
            if self.coef[i] != 0.0:
                if self.coef[i] >= 0:                   # 상수항의 부호 판별
                    print(" + ", end='')
                else:
                    print(" - ", end='')
                print("%0.2f" % (abs(self.coef[i])))
            else:                                       # 상수항이 0일 경우 0 출력하지 않고 줄바꿈
                print()
        else:
            if self.coef[i] != 0.0:
                if i == 0:
                    print("%0.2f x^%d" % (self.coef[i], self.degree - i - 1), end='')
                else:
                    if self.coef[i] >= 0:
                        print(" + ", end='')
                    else:
                        print(" - ", end='')
                    print("%0.2f x^%d" % (abs(self.coef[i]), self.degree - i - 1), end='')

poly1 형태로 저장된 다항식 값을 사람이 보기 쉬운 다항식 형태로 표시해주는 메소드이다.
최고 차항의 계수가 양수인지 음수인지, 상수항이 0인지 아닌지, 각 항의 계수가 양수인지 음수인지 등을 판단하고,
그에 따라 각 항에 알맞은 부호를 부여한다.

🛠 find_val( )

def find_val(self, x):
    temp_degree = self.degree
    val = 0
    for i in range(self.degree):
        temp = 1
        for j in range(temp_degree - 1):
            temp *= x
        if temp_degree == 1:
            temp = self.coef[i]
        else:
            temp = temp * self.coef[i]
        val += temp
        temp_degree -= 1
    print('결과 값은 %0.1f' %val)

다항식의 x에 값을 대입하여 해를 찾아주는 메소드이다.
최고차항부터 x에 대입한 값을 차수 번 만큼 제곱해주고, 제곱한 값과 해당 차수의 계수를 곱한다.
상수의 경우 차수 곱 없이 계수의 값만 저장해준다.
그렇게 구해진 각 항의 계산값을 val 에 더해준다.
이때 temp_degree 는 현재 항의 해를 찾기 위한 다항식의 index값이다.

🛠 poly1_add( )

def poly1_add(a,b):
    z = []                  # 두 다항식의 덧셈의 결과값을 담아 줄 리스트
    apos = bpos = 0         # 두 다항식의 현재 위치
    degree_a = a.degree     # 다항식 a의 차수(ex. 2차, 3차, 4차 ...)
    degree_b = b.degree     # 다항식 b의 차수

    while (apos < degree_a) or (bpos < degree_b):
        if degree_a > degree_b:
            z.append(a.coef[apos])
            apos += 1
            degree_a -= 1
        elif degree_a == degree_b:              # 두 다항식에서 현재 위치한 항의 차수가 같은 경우
            z.append(a.coef[apos]+b.coef[bpos]) # 두 항의 계수를 더해준다
            apos += 1
            bpos += 1
        else:
            z.append(b.coef[bpos])
            bpos += 1
            degree_b -= 1
    return poly1(z)

두개의 다항식을 매개변수로 받아서 더해주는 함수이다.

🛠 poly1_mul( )

def poly1_mul(a, b):
    x = []                  # a의 최고차항 * b다항식 전체
    degree_a = a.degree
    degree_b = b.degree

    apos = 0
    for i in range(degree_b):
        x.append(a.coef[apos] * b.coef[i])
    for i in range(degree_a - 1):
        x.append(0)

    x = poly1(x)
    degree_a -= 1
    apos += 1

    while(apos < a.degree):
        y = []              # a의 최고차항 이하의 항 * b다항식 전체
        for i in range(degree_b):
            y.append(a.coef[apos] * b.coef[i])
        for i in range(degree_a - 1):
            y.append(0)
        y = poly1(y)

        x = poly1_add(x, y) # a + b
        apos += 1
        degree_a -= 1
    return x

두개의 다항식을 매개변수로 받아서 곱해주는 함수이다.
첫 번째 다항식인 a 의 각항을 두번째 다항식 b 와 곱해주고, 그 결과값들을 poly1_add함수를 통해 모두 더해주는 방식으로 작동한다.

1) a의 최고차항과 b다항식 전체를 곱해준 결과값을 x 리스트에 넣어준다.
2) 이후 순서대로 a의 최고차항 이하의 항들과 b다항식 전체를 곱한 값을 y 리스트에 넣어준다.
3) x와 y를 poly1_add 함수를 통해 더해준다.
4) a의 마지막 항까지 위의 과정을 반복해준다.

🛠 print_val( )

def print_val():
    while True:
        e = list(map(float, input("수식에 값을 넣으세요 ").split(' ')))
        if e[0] == 1:           # 수식1을 선택할 경우
            a.find_val(e[1])    
        elif e[0] == 2:         # 수식2를 선택할 경우
            b.find_val(e[1])    
        elif e[0] == 3:         # 수식3(수식1 + 수식2)을 선택할 경우
            c.find_val(e[1])  
        elif e[0] == 4:         # 수식4(수식1 * 수식2)를 선택할 경우
            d.find_val(e[1])
        else:                   # 범위(1~4)를 벗어난 값이 입력된 경우
            print('잘못된 값을 입력하셨습니다!')

사용자가 선택한 다항식에 값을 대입할 경우 그 결과 값을 출력해주는 함수.
우선 첫번째로 입력 받은 숫자를 통해 몇번째 다항식에 값을 대입할지 판단하는데,
이때 범위(1~4)를 벗어나는 숫자가 입력되면 값을 다시 입력받는다.
두번째로 입력 받은 숫자를 find_val 메소드를 통해 선택한 다항식에 대입하여 그 결과값을 구해준다.

📌 실행결과

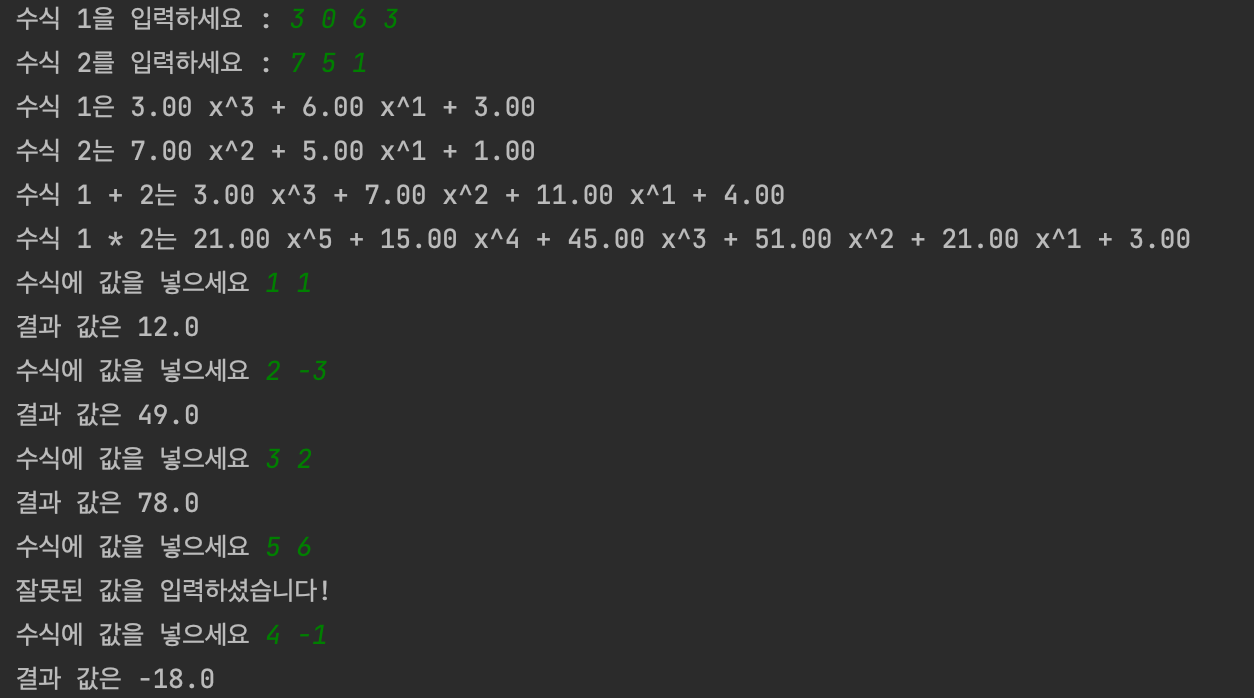
📌 전체코드

class poly1():
    def __init__(self, coef):
        self.coef = coef
        self.degree = len(coef)

    def print_poly1(self):
        for i in range(self.degree):
            if i == self.degree - 1:                        # 상수항인지 판별
                if self.coef[i] != 0.0:
                    if self.coef[i] >= 0:                   # 상수항의 부호 판별
                        print(" + ", end='')
                    else:
                        print(" - ", end='')
                    print("%0.2f" % (abs(self.coef[i])))
                else:                                       # 상수항이 0일 경우 0 출력하지 않고 줄바꿈
                    print()
            else:
                if self.coef[i] != 0.0:
                    if i == 0:
                        print("%0.2f x^%d" % (self.coef[i], self.degree - i - 1), end='')
                    else:
                        if self.coef[i] >= 0:
                            print(" + ", end='')
                        else:
                            print(" - ", end='')
                        print("%0.2f x^%d" % (abs(self.coef[i]), self.degree - i - 1), end='')

    def find_val(self, x):
        temp_degree = self.degree
        val = 0
        for i in range(self.degree):
            temp = 1
            for j in range(temp_degree - 1):
                temp *= x
            if temp_degree == 1:
                temp = self.coef[i]
            else:
                temp = temp * self.coef[i]
            val += temp
            temp_degree -= 1
        print('결과 값은 %0.1f' %val)

def poly1_add(a,b):
    z = []                  # 두 다항식의 덧셈의 결과값을 담아 줄 리스트
    apos = bpos = 0         # 두 다항식의 현재 위치
    degree_a = a.degree     # 다항식 a의 차수(ex. 2차, 3차, 4차 ...)
    degree_b = b.degree     # 다항식 b의 차수

    while (apos < degree_a) or (bpos < degree_b):
        if degree_a > degree_b:
            z.append(a.coef[apos])
            apos += 1
            degree_a -= 1
        elif degree_a == degree_b:              # 두 다항식에서 현재 위치한 항의 차수가 같은 경우
            z.append(a.coef[apos]+b.coef[bpos]) # 두 항의 계수를 더해준다
            apos += 1
            bpos += 1
        else:
            z.append(b.coef[bpos])
            bpos += 1
            degree_b -= 1
    return poly1(z)

def poly1_mul(a, b):
    x = []                  # a의 최고차항 * b다항식 전체
    degree_a = a.degree
    degree_b = b.degree

    apos = 0
    for i in range(degree_b):
        x.append(a.coef[apos] * b.coef[i])
    for i in range(degree_a - 1):
        x.append(0)

    x = poly1(x)
    degree_a -= 1
    apos += 1

    while(apos < a.degree):
        y = []              # a의 최고차항 이하의 항 * b다항식 전체
        for i in range(degree_b):
            y.append(a.coef[apos] * b.coef[i])
        for i in range(degree_a - 1):
            y.append(0)
        y = poly1(y)

        x = poly1_add(x, y) # a + b
        apos += 1
        degree_a -= 1
    return x

def print_val():
    while True:
        e = list(map(float, input("수식에 값을 넣으세요 ").split(' ')))
        if e[0] == 1:           # 수식1을 선택할 경우
            a.find_val(e[1])
        elif e[0] == 2:         # 수식2를 선택할 경우
            b.find_val(e[1])
        elif e[0] == 3:         # 수식3(수식1 + 수식2)을 선택할 경우
            c.find_val(e[1])
        elif e[0] == 4:         # 수식4(수식1 * 수식2)를 선택할 경우
            d.find_val(e[1])
        else:                   # 범위(1~4)를 벗어난 값이 입력된 경우
            print('잘못된 값을 입력하셨습니다!')

a = list(map(float, input("수식 1을 입력하세요 : ").split(' ')))
while len(a) > 6:
    a = list(map(float, input("최대 차수를 초과하였습니다. 다시 입력해주세요! : ").split(' ')))
b = list(map(float, input("수식 2를 입력하세요 : ").split(' ')))
while len(b) > 6:
    b = list(map(float, input("최대 차수를 초과하였습니다. 다시 입력해주세요! : ").split(' ')))

a = poly1(a)
b = poly1(b)
c = poly1_add(a, b)
d = poly1_mul(a, b)

print('수식 1은 ', end='')
a.print_poly1()
print('수식 2는 ', end='')
b.print_poly1()
print('수식 1 + 2는 ', end='')
c.print_poly1()
print('수식 1 * 2는 ', end='')
d.print_poly1()

print_val()

2. 다항식 중 계수가 0이 아닌 항만을 배열에 저장하는 방식

``` class poly2(): def __init__(self, coef): self.coef_deg = coef # 다항식의 각 항의 계수와 차수를 나타내는 변수 self.degree = len(coef) # 각 다항식의 항의 개수를 나타낼 변수 ``` 다항식을 표현하기 위해 **poly2** 클래스를 선언해준다. **coef_deg** : 다항식의 각 항의 계수(coef)와 차수(deg)를 담아주는 변수이다. **degree** : 각 다항식의 항의 개수를 나타낼 변수이다.

🛠 print_poly2( )

def print_poly2(self):
    for i in range(self.degree):
        if i == self.degree - 1:                 # 맨 마지막 항의
            if self.coef_deg[i][0] != 0.0:       # 계수가 0이 아닐 경우
                if self.coef_deg[i][0] >= 0:     # 항의 부호 판별
                    print(" + ", end='')         # 양수일 경우엔 '+'를
                else:
                    print(" - ", end='')         # 음수일 경우엔 '-'를

                if self.coef_deg[i][1] == 0:     # 상수일 경우엔 계수만 출력한다
                    print("%0.2f" % (abs(self.coef_deg[i][0])))
                else:                            # 상수가 아닐 경우엔 "계수 x^차수"형태로 출력한다.
                    print("%0.2f x^%d" % (abs(self.coef_deg[i][0]), self.coef_deg[i][1]))
            else:
                print()                          # 맨 마지막 항이 상수가 아니고 계수가 0일 경우엔 아무것도 출력하지 않는다
        else:
            if self.coef_deg[i][0] != 0.0:       # 계수가 0일경우 아무것도 출력하지 않는다
                if i == 0:                       # 첫 항의 부호를 출력하기 위해 따로 출력
                    print("%0.2f x^%d" % (self.coef_deg[i][0], self.coef_deg[i][1]), end="")
                else:
                    if self.coef_deg[i][0] >= 0:
                        print(" + ", end='')
                    else:
                        print(" - ", end='')
                    print("%0.2f x^%d" % (abs(self.coef_deg[i][0]), self.coef_deg[i][1]), end="")

2차원 리스트로 저장된 다항식을 진짜 다항식 형태로 변환해주는 메소드이다.

1) 우선 다항식의 마지막 항이 상수이고, 그 값이 0인 경우에는 굳이 출력을 하지 않도록 코드를 수정하였다.
2) 또한 마지막 항이 상수는 아니지만 계수가 0일 경우에도 아무것도 출력하지 않도록 수정하였다.
3) 마지막으로 맨 첫번째 항의 계수의 부호도 표시할 수 있도록 코드를 수정하였다.

🛠 find_val( )

def find_val(self, x):
    val = 0                                         # 최종 결과 값을 반영해 줄 변수 val 선언
    for i in range(self.degree):                    # 각 항을 돌며
        temp = 1
        for j in range(int(self.coef_deg[i][1])):   # 각 항의 차수 만큼(횟수)
            temp *= x                               # 입력받은 x의 값을 곱해준다
        if self.coef_deg[i][1] == 0:                # 차수가 0일 경우는 상수이므로
            temp = self.coef_deg[i][0]              # 해당 항의 계수가 곧 temp값이 된다
        else:
            temp = temp * self.coef_deg[i][0]
        val += temp                                 # val에 temp값을 더해준다
    print('결과 값은 %0.2f' %val)

다항식의 x에 값을 대입하여 해를 찾아주는 메소드이다.
우선 최종 결과 값을 담을 변수 val 을 선언하고 0으로 초기화해준다.
그리고 각 항의 계산 결과값을 담을 변수 temp 를 선언하고 1로 초기화해준다.
전체 항을 돌며 각 항마다 각 항의 차수 만큼(횟수) 반복하여 입력 받은 값을 temp에 곱해주고, 그 값에 다시 각 항의 계수를 곱해준다.
이때 차수가 0인 항은 상수이므로 해당 항의 계수가 곧 temp값이 된다.
그렇게 구해진 각 temp값들을 val에 더해주면 최종 계산 결과값이 될 것이다.

🛠 poly2_add( )

def poly2_add(a,b):
    z = []
    apos = bpos = 0
    term_a = a.degree
    term_b = b.degree

    while(apos < term_a) and (bpos < term_b):
        if a.coef_deg[apos][1] > b.coef_deg[bpos][1]:
            z.append([a.coef_deg[apos][0], a.coef_deg[apos][1]])
            apos += 1
        elif a.coef_deg[apos][1] == b.coef_deg[bpos][1]:
            z.append([a.coef_deg[apos][0] + b.coef_deg[bpos][0], a.coef_deg[apos][1]])
            apos += 1
            bpos += 1
        else:
            z.append([b.coef_deg[bpos][0], b.coef_deg[bpos][1]])
            bpos += 1

        if apos >= term_a:
            while bpos < term_b:
                z.append([b.coef_deg[bpos][0], b.coef_deg[bpos][1]])
                bpos += 1
        elif bpos >= term_b:
            while apos < term_a:
                z.append([a.coef_deg[apos][0], a.coef_deg[apos][1]])
                apos += 1
    return poly2(z)

입력 받은 두 다항식을 서로 더하고, 그 결과 값을 반환하는 함수이다.

🛠 poly2_mul( )

def poly2_mul(a, b):
    x = []                                                                                           # 최종 결과 값을 담아 줄 빈 리스트 x 선언
    apos = 0
    for i in range(b.degree):
        x.append([a.coef_deg[apos][0]*b.coef_deg[i][0], a.coef_deg[apos][1] + b.coef_deg[i][1]])     # 각 항의 계수끼리는 곱하고, 차수끼리는 더해준다.
    x = poly2(x)                                                                                     # 위 연산의 결과 값을 x에 담아준다
    apos += 1

    while (apos < a.degree):
        y = []                                                                                       # 중간 결과 값을 담아 줄 빈 리스트 y 선언
        for i in range(b.degree):
            y.append([a.coef_deg[apos][0]*b.coef_deg[i][0], a.coef_deg[apos][1] + b.coef_deg[i][1]]) # 위와 같은 방식의 연산 수행
        y = poly2(y)                                                                                 # 위 연산의 결과 값을 y에 담아준다

        x = poly2_add(x, y)                                                                          # x와 y를 더해준 값을 x에 담아준다
        apos += 1
    return x

우선 최종 결과값을 담게 될 리스트 x 를 선언해준다.
그리고 a 의 첫번째 요소(ex. [1, 2])와 b 전체에 대하여
coef_deg[i][0] , 즉 각 항의 계수에 대해서는 곱셈을,
coef_deg[i][1] , 즉 차수에 대해서는 덧셈 연산을 수행하고 그 결과값을 리스트 x에 추가 해준다.

다음으론 while문 안에 중간 결과 값을 반영할 리스트 y 를 선언해준다.
a의 두번째 요소부터 위와 같은 방식의 연산을 수행한 결과값을 y에 추가 해주고,
이를 poly2_add( ) 함수를 통해 x와 더해주고 그 결과값을 다시 x에 대입한다.
위와 같은 과정을 a의 마지막 요소까지 반복해서 수행하고, 연산이 모두 끝난 후에는 리스트 x를 반환하도록 한다.

📌 실행결과

📌 전체코드

class poly2():
    def __init__(self, coef):
        self.coef_deg = coef        # 다항식의 각 항의 계수와 차수를 나타내는 변수
        self.degree = len(coef)     # 각 다항식의 항의 개수를 나타낼 변수

    def print_poly2(self):
        for i in range(self.degree):
            if i == self.degree - 1:                 # 맨 마지막 항의
                if self.coef_deg[i][0] != 0.0:       # 계수가 0이 아닐 경우
                    if self.coef_deg[i][0] >= 0:     # 항의 부호 판별
                        print(" + ", end='')         # 양수일 경우엔 '+'를
                    else:
                        print(" - ", end='')         # 음수일 경우엔 '-'를

                    if self.coef_deg[i][1] == 0:     # 상수일 경우엔 계수만 출력한다
                        print("%0.2f" % (abs(self.coef_deg[i][0])))
                    else:                            # 상수가 아닐 경우엔 "계수 x^차수"형태로 출력한다.
                        print("%0.2f x^%d" % (abs(self.coef_deg[i][0]), self.coef_deg[i][1]))
                else:
                    print()                          # 맨 마지막 항이 상수가 아니고 계수가 0일 경우엔 아무것도 출력하지 않는다
            else:
                if self.coef_deg[i][0] != 0.0:       # 계수가 0일경우 아무것도 출력하지 않는다
                    if i == 0:                       # 첫 항의 부호를 출력하기 위해 따로 출력
                        print("%0.2f x^%d" % (self.coef_deg[i][0], self.coef_deg[i][1]), end="")
                    else:
                        if self.coef_deg[i][0] >= 0:
                            print(" + ", end='')
                        else:
                            print(" - ", end='')
                        print("%0.2f x^%d" % (abs(self.coef_deg[i][0]), self.coef_deg[i][1]), end="")

    def find_val(self, x):
        val = 0                                         # 최종 결과 값을 반영해 줄 변수 val 선언
        for i in range(self.degree):                    # 각 항을 돌며
            temp = 1
            for j in range(int(self.coef_deg[i][1])):   # 각 항의 차수 만큼(횟수)
                temp *= x                               # 입력받은 x의 값을 곱해준다
            if self.coef_deg[i][1] == 0:                # 차수가 0일 경우는 상수이므로
                temp = self.coef_deg[i][0]              # 해당 항의 계수가 곧 temp값이 된다
            else:
                temp = temp * self.coef_deg[i][0]
            val += temp                                 # val에 temp값을 더해준다
        print('결과 값은 %0.2f' %val)

def print_val():
    while True:
        e = list(map(float, input("수식에 값을 넣으세요 ").split(' ')))
        if e[0] == 1:
            a.find_val(e[1])
        elif e[0] == 2:
            b.find_val(e[1])
        elif e[0] == 3:
            c.find_val(e[1])
        elif e[0] == 4:
            d.find_val(e[1])
        else:
            print('잘못된 값을 입력하셨습니다!')

def poly2_add(a,b):
    z = []
    apos = bpos = 0
    term_a = a.degree
    term_b = b.degree

    while(apos < term_a) and (bpos < term_b):
        if a.coef_deg[apos][1] > b.coef_deg[bpos][1]:
            z.append([a.coef_deg[apos][0], a.coef_deg[apos][1]])
            apos += 1
        elif a.coef_deg[apos][1] == b.coef_deg[bpos][1]:
            z.append([a.coef_deg[apos][0] + b.coef_deg[bpos][0], a.coef_deg[apos][1]])
            apos += 1
            bpos += 1
        else:
            z.append([b.coef_deg[bpos][0], b.coef_deg[bpos][1]])
            bpos += 1

        if apos >= term_a:
            while bpos < term_b:
                z.append([b.coef_deg[bpos][0], b.coef_deg[bpos][1]])
                bpos += 1
        elif bpos >= term_b:
            while apos < term_a:
                z.append([a.coef_deg[apos][0], a.coef_deg[apos][1]])
                apos += 1
    return poly2(z)

def poly2_mul(a, b):
    x = []                                                                                           # 최종 결과 값을 담아 줄 빈 리스트 x 선언
    apos = 0
    for i in range(b.degree):
        x.append([a.coef_deg[apos][0]*b.coef_deg[i][0], a.coef_deg[apos][1] + b.coef_deg[i][1]])     # 각 항의 계수끼리는 곱하고, 차수끼리는 더해준다.
    x = poly2(x)                                                                                     # 위 연산의 결과 값을 x에 담아준다
    apos += 1

    while (apos < a.degree):
        y = []                                                                                       # 중간 결과 값을 담아 줄 빈 리스트 y 선언
        for i in range(b.degree):
            y.append([a.coef_deg[apos][0]*b.coef_deg[i][0], a.coef_deg[apos][1] + b.coef_deg[i][1]]) # 위와 같은 방식의 연산 수행
        y = poly2(y)                                                                                 # 위 연산의 결과 값을 y에 담아준다

        x = poly2_add(x, y)                                                                          # x와 y를 더해준 값을 x에 담아준다
        apos += 1
    return x

a = list(map(float, input("수식 1을 입력하세요 : ").split(' ')))
while a[1] > 6: # 최고 차항이 6이상이면 값을 다시 입력받는다
    a = list(map(float, input("최대 차수를 초과하였습니다. 다시 입력해주세요! : ").split(' ')))
temp = []
for i in range(0, len(a), 2):
    temp.append(a[i:i+2])
a = poly2(temp)

b = list(map(float, input("수식 2를 입력하세요 : ").split(' ')))
while b[1] > 6: # 최고 차항이 6이상이면 값을 다시 입력받는다
    b = list(map(float, input("최대 차수를 초과하였습니다. 다시 입력해주세요! : ").split(' ')))
temp = []
for i in range(0, len(b), 2):
    temp.append(b[i:i+2])
b = poly2(temp)

c = poly2_add(a, b)
d = poly2_mul(a, b)

print('수식 1은 ', end='')
a.print_poly2()
print('수식 2는 ', end='')
b.print_poly2()
print('수식 1 + 2는 ', end='')
c.print_poly2()
print('수식 1 * 2는 ', end='')
d.print_poly2()

print_val()