🤔복잡도란?

복잡도란 알고리즘의 성능 평가 및 효율성을 나타내는 척도로써, 시간 복잡도와 공간 복잡도로 나눌 수 있다.

• 시간 복잡도 : 얼마나 빠르게 실행되는가?
• 공간 복잡도 : 얼마나 많은 저장 공간이 필요한가?

좋은 알고리즘은 실행 시간이 짧으면서 저장 공간도 적게 쓰는 알고리즘이다!

그러나 둘 다 만족시키기는 아래와 같은 이유로 어려움이 있다.

• 시간과 공간은 반비례적 경향이 있다
• 최근 대용량 시스템이 보편화되면서 공간 복잡도보다는 시간 복잡도가 우선이 된다.
• 그래서 알고리즘은 시간 복잡도가 중심이다.

---

💡공간 복잡도(Space Complexity)

알고리즘이 실행되는 동안 필요한 추가 메모리의 양을 나타낸 것.
입력 크기와 상관없이 알고리즘이 필요로 하는 메모리의 양을 나타낸 것이다.

---

✅n! 팩토리얼 구하기 : 반복문

n! = 1 x 2 x ... x n

public class FactorialExample {

    public static int factorial(int n) {
        int fac = 1;
        for (int i = 2; i <= n; i++) {
            fac = fac * i;
        }
        return fac;
    }

    public static void main(String[] args) {
        int result = factorial(3);
        System.out.println("3! = " + result);
    }
}

• 구현 : 반복문
• n의 값에 상관 없이 변수 n, 변수 fac, 변수 i만 필요함
• 즉, 입력크기 n이 아무리 커져도 추가로 필요한 변수 개수는 변하지 않는다
  ➡️공간복잡도는 O(1)

---

✅n! 팩토리얼 구하기 : 재귀함수

n! = 1 x 2 x ... x n

public class FactorialExample {

   public static int factorial(int n) {
       if (n > 1) {
           return n * factorial(n - 1);
       } else {
           return 1;
       }
   }

   public static void main(String[] args) {
       int result = factorial(3);
       System.out.println(result); // 출력: 6
   }
}

• 구현 : 재귀함수
• 재귀 함수를 사용하였으므로, n에 따라 변수 n이 n개가 만들어지게됨.
• 재귀 호출을 할때마다 스택 프레임이 생긴다.
• factorial(3) 호출 시,

  factorialRecursive(3)
   -> factorialRecursive(2)
     -> factorialRecursive(1)

• 호출 깊이가 n이므로 스택 메모리를 n개 사용
  ➡️공간복잡도는 O(n)

---

💡시간 복잡도(Time Complexity)

알고리즘이 실행되는 동안 수행하는 기본적인 연산 횟수의 총량.

• 시간복잡도라고 해서 실제 걸리는 시간(초 단위)로 표현하지 않는다.
• 속도는 컴퓨터라는 하드웨어가 결정하기 때문에 같은 알고리즘이더라도 내 컴퓨터와 친구의 컴퓨터에서 속도가 다를 수 있기 때문에 실제 걸리는 시간은 무의미함
• 따라서 알고리즘의 속도는 완료까지 걸리는 절차의 수(연산 횟수)로 결정한다.

---

💡빅오(Big-O) 표기법

알고리즘의 효율성을 표기해주는 표기법

✅점근 표기법

• Big-O(빅-오) : 최대 이만큼 느려질 수 있어요! ➡️최악/상한
• Big-Ω(빅-오메가) : 적어도 이만큼은 걸려요! ➡️최소/하한
• Big-Θ(빅-세타) : 대략 항상 이정도 걸려요! ➡️빅-오와 빅-세타가 같은 차수일 때 그 차수

📌빅오 표기법은 최악의 경우를 고려하므로 프로그램이 실행되는 과정에서 소요되는 최악의 시간까지 고려가능하므로 가장 자주 사용된다.

---

💡빅오(Big-O) 표기법의 종류

1️⃣O(1)

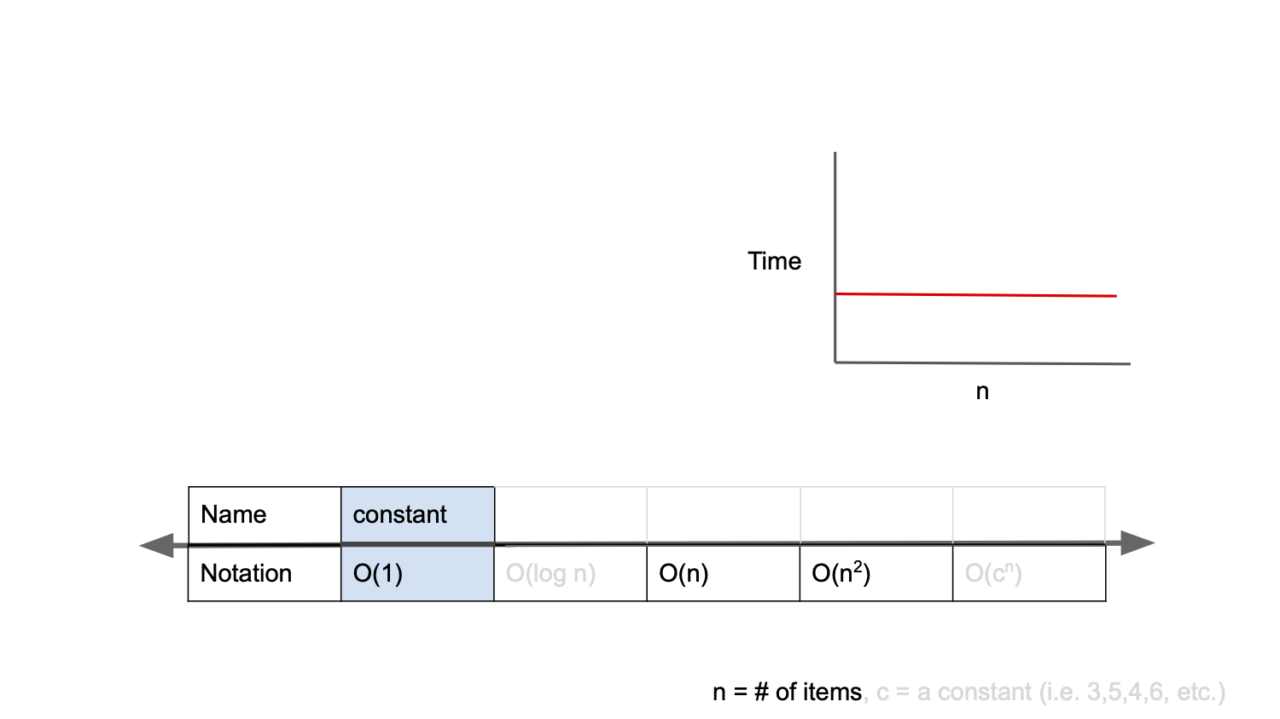
O(1)는 일정한 복잡도라고하며, 입력값이 증가하더라도 시간이 늘어나지 않는다.

---

2️⃣O(n)

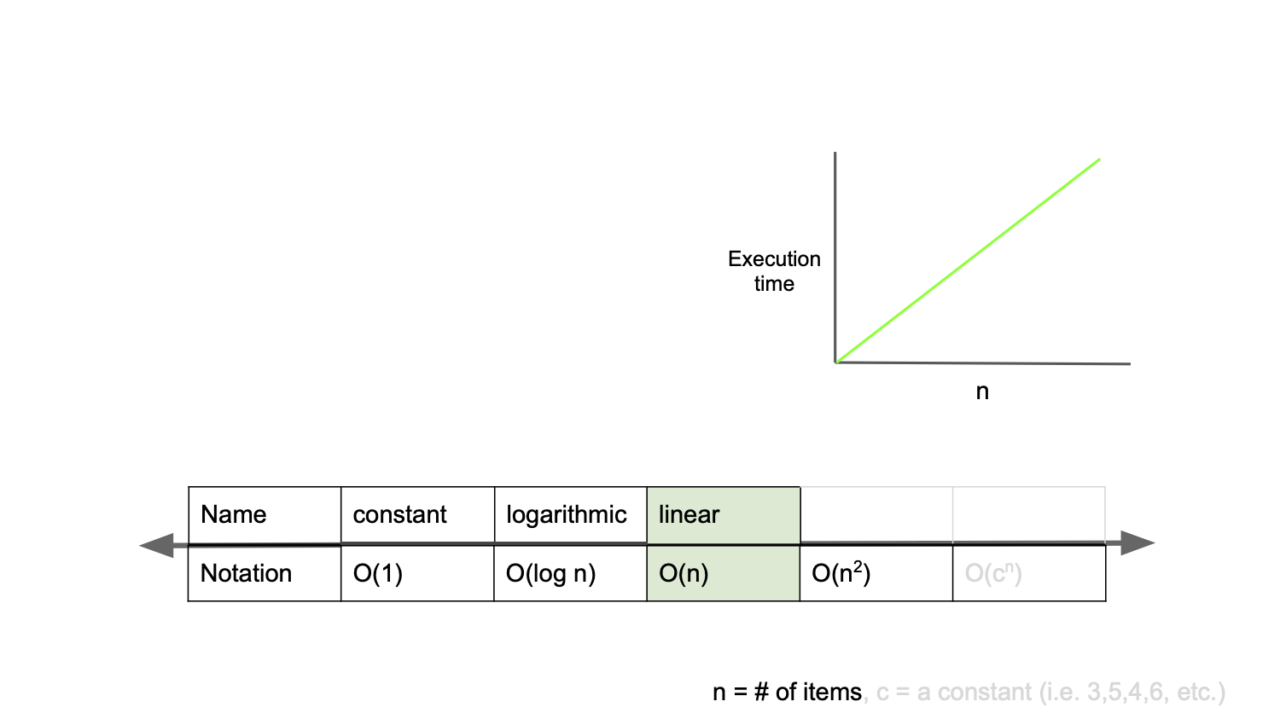
O(n)은 선형 복잡도라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.

• 예를 들어, 입력 값이 1일 때 1초의 시간이 걸리고, 입력값을 100배로 증가시켰을 때 100초가 걸리는 알고리즘을 구현했다면, 그 알고리즘은 O(n)의 시간 복잡도를 가진다고 할 수 있다.

---

3️⃣O(log n)

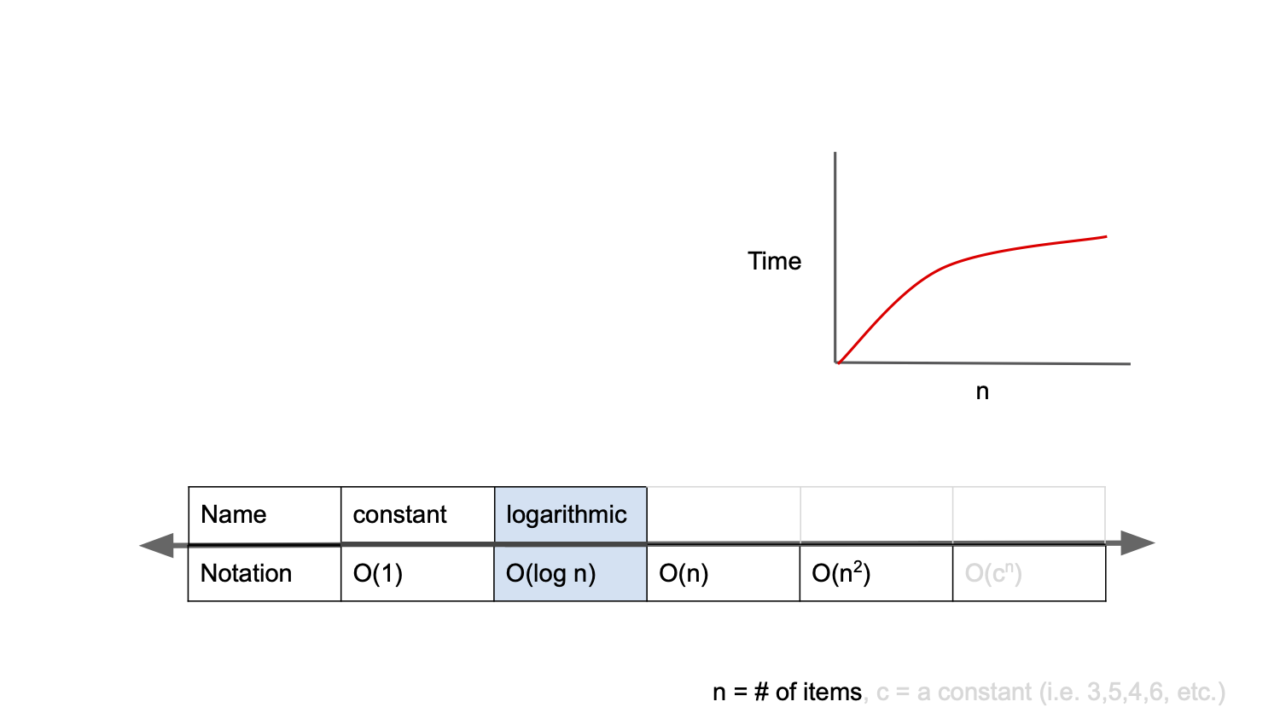
O(log n)은 로그복잡도라고 부르며, 빅오 표기법 중 O(1) 다음으로 빠진 시간 복잡도를 가진다.

---

4️⃣O(n²)

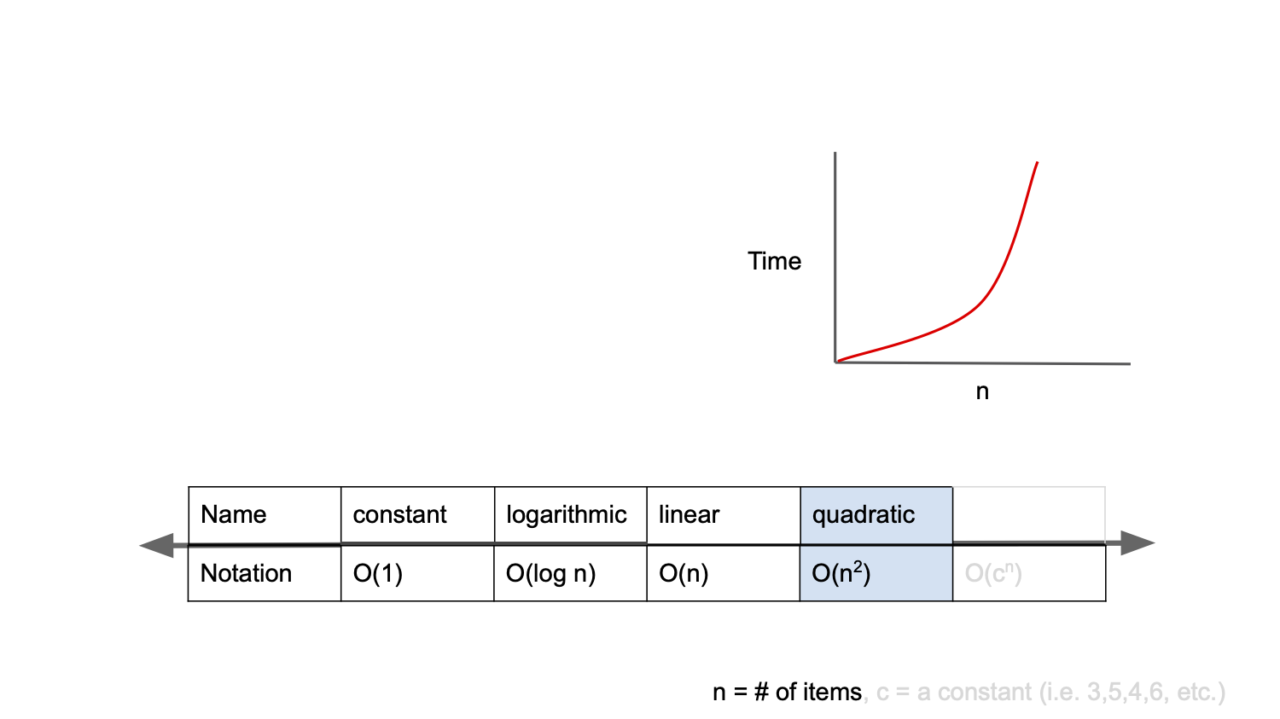
O(n²)는 2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.

• 예를 들어, 입력값이 1일 경우, 1초가 걸리던 알고리즘에 5라는 값을 주었더니 25초가 걸리게 된다면, 이 알고리즘의 시간 복잡도는 O(n²)라고 표현한다.

---

5️⃣O(2ⁿ)

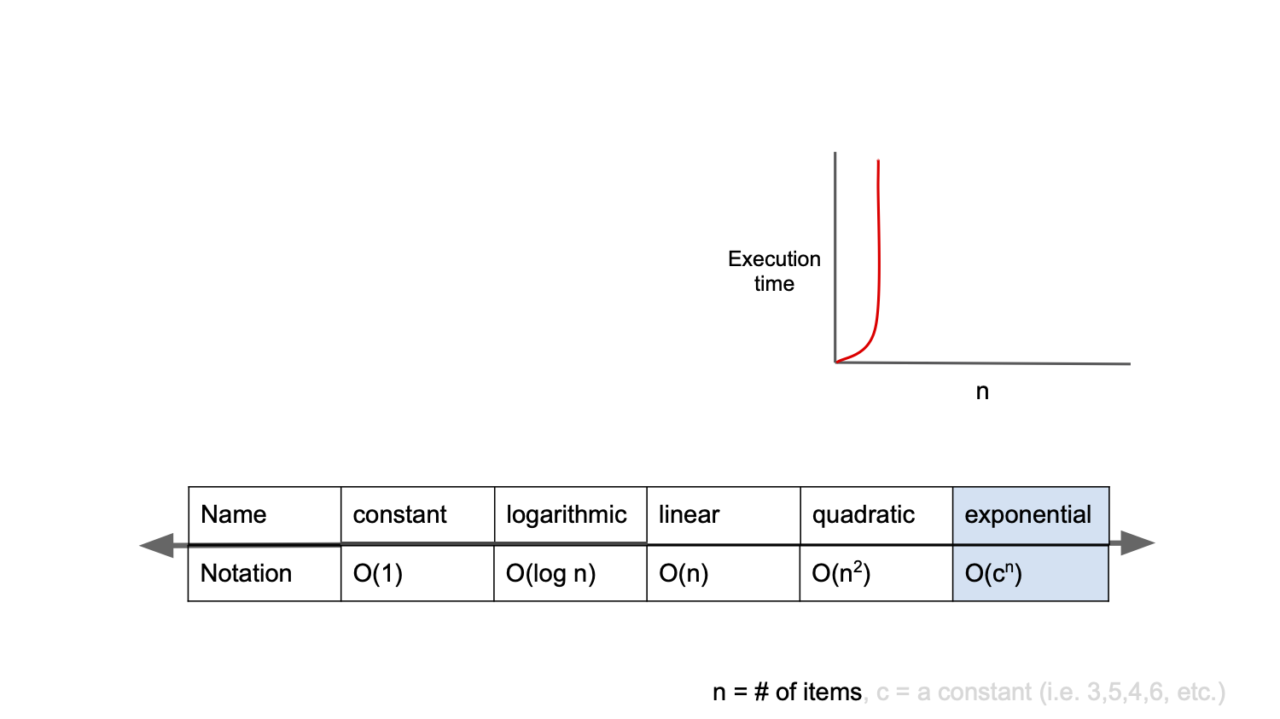
O(2n)은 기하급수적 복잡도라고 부르며, 빅오 표기법중 가장 느린 시간복잡도를 가진다.

---

☑️정리

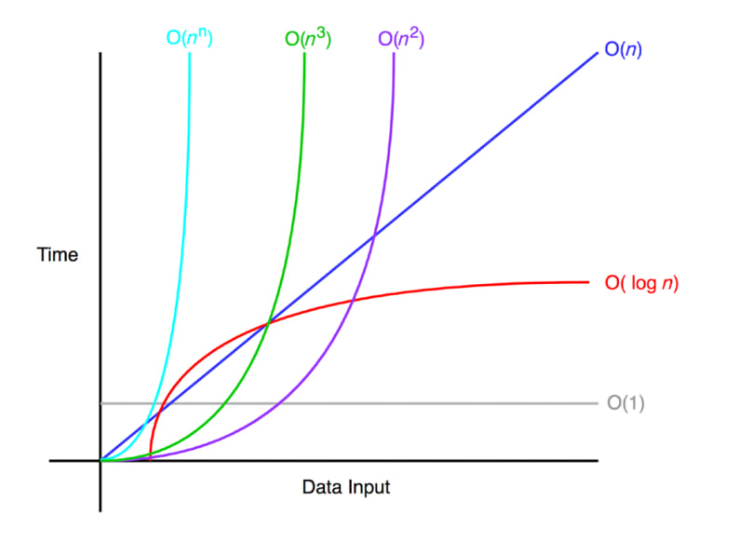
• 시간복잡도의 성능은 다음과 같다.
  
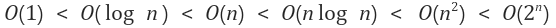
• 상수함수 < 로그함수 < 선형함수 < 다항함수 < 지수함수

표기법	소개	대표 예시
O(1)	입력 크기와 관계없이 항상 일정한 시간이 걸림	▪️배열에서 인덱스 접근 ▪️해시테이블에서 키로 값 가져오기
O(n)	입력 크기만큼 시간이 걸림	▪️배열 전체 순회(for) ▪️연결 리스트 탐색
O(log n)	입력 크기가 커질수록 조금씩만 시간이 늘어남	▪️이진 탐색 ▪️균행 이진탐색 트리에서 탐색
O(n²)	입력이 조금만 커져도 실행시간이 크게 증가	▪️버블 정렬 ▪️삽입 정렬 ▪️선택 정렬
O(2ⁿ)	입력 크기가 조금만 커져도 시간이 폭발적으로 증가	▪️부분집합 구하기 ▪️피보나치 수열(재귀)
O(n log n)	효율적인 정렬 알고리즘의 대표적인 시간 복잡도	▪️병합 정렬 ▪️퀵 정렬 ▪️힙 정렬(최악은 O(2ⁿ)) ▪️이진 탐색 트리를 이용한 정렬

---

☑️정렬 알고리즘 시간 복잡도 비교

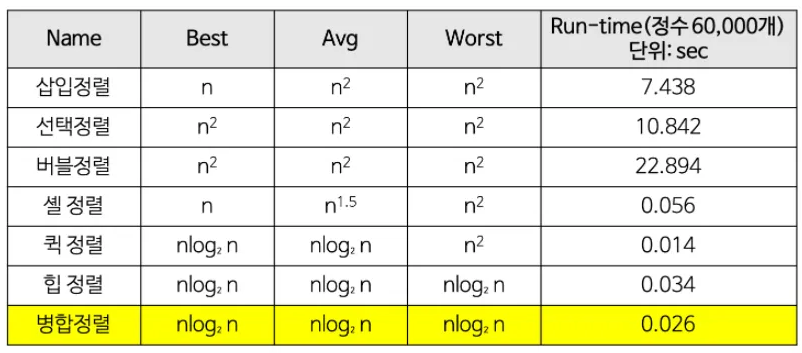
• 단순 (구현 간단)하지만 비효율적인 방법
  - 삽입 정렬, 선택 정렬, 버블 정렬
• 복잡하지만 효율적인 방법
  - 퀵 정렬, 힙 정렬, 합병 정렬, 기수 정렬