🌳 트리(Tree)란?
트리란 계층적인 구조를 나타내는 자료구조로, 노드(Node)와 노드를 연결해주는 간선(Edge)로 이루어져 있다. 노드의 개수가 N개일 때, 간선의 개수는 항상 N-1 이다.
💭트리에서 사용되는 용어들
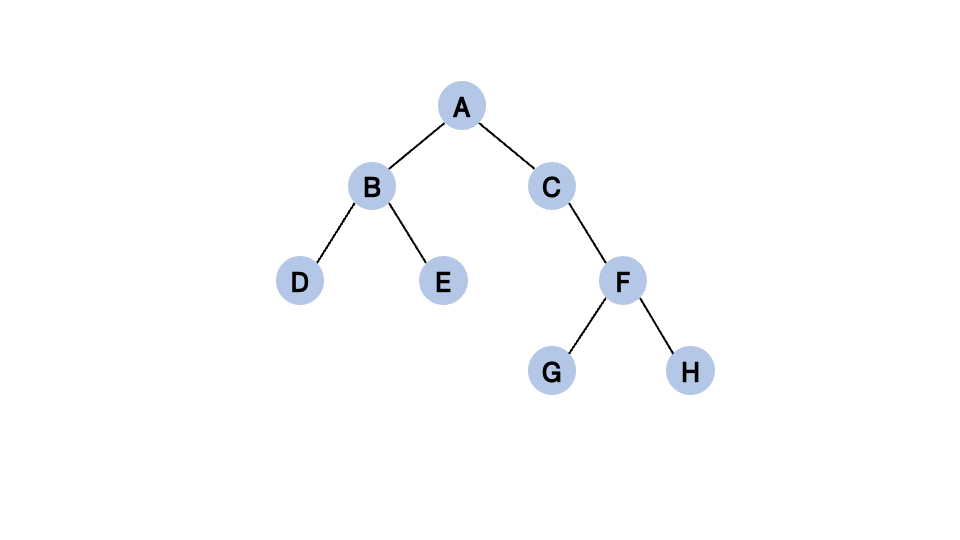
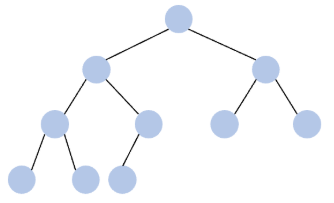
1. 루트 (Root) : 최상단 노드 (A)
2. 자식(Child) : 부모(Parent)를 가진 노드 (B, D, E, C, F, G, H)
3. 리프(Leaf) : 자식이 없는 말단 노드 (D, E, G, H)
4. 내부 노드(internal node) : 자식 노드가 하나라도 존재하는 노드로, 리프 노드가 아닌 노드 (A,B,C,F)
5. 형제(sibling) : 같은 레벨에 위치한 노드들의 관계 (B-D, C-D-F, G-H)
6. 조상(ancestor)-후손(descendant) : (D의 조상은 A, B이며, H의 조성은 F, C, A)
7. 차수(degree) : 자식 노드의 개수 (F의 차수는 2, G의 차수는 0)
8. 레벨(level) : 루트 노드로부터 얼마나 떨어져있는지를 나타냄 (B와 C의 레벨은 1, D의 레벨은 2, G의 레벨은 3)
9. 높이(height) : 루트 노드부터 시작해서 리프 노드까지의 거리 (예시 트리의 높이는 4)
10. 서브트리(subtree) : 트리 안의 트리. 특정 노드들을 기준으로 하여 해당 노드의 후손들로 구성한 트리
🔄트리 순회
트리의 순회란 정해진 순서에 따라 트리의 모든 노드를 한번씩 방문하는 작업을 말한다.
깊이 우선 탐색과 너비 우선 탐색으로 나뉜다.
깊이 우선 탐색(DFS, Depth-Firsh Search)
왼쪽/오른쪽 자식을 따라 끝까지 내려갔다가 다시 올라오는 방식
Root 기준이라는 것을 잊지말것!
1. 전위 순회(Pre-order traverse)
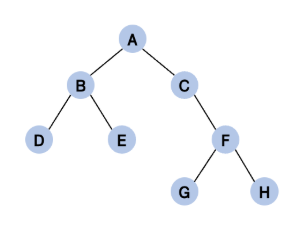
- 순서 : Root → Left → Right
- 예시 트리 순서 : A → B → D → E → C → F → G → H
2. 중위 순회(In-order traverse)

- 순서 : Left → Root → Right
- 예시 트리 순서 : D → B → E → A → C → G → F → H
3. 후위 순회(Postorder traverse)

- 순서 : Left → Right → Root
- 예시 트리 순서 : D → E → B → G → H → F → C → A
너비 우선 탐색(BFS, Breadth-First Search)
레벨 단위로 방문(큐 사용)
1. 레벨 순회(Level-order traverse)
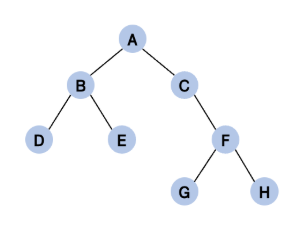
- 순서 : 위에서 아래, 왼쪽에서 오른쪽. 낮은 레벨에 있는 노드들 모두 방문 후 다음 레벨로 이동
- 예시 트리 순서 : A → B → C → D → E → F → G → H
🌲이진 트리(Binary Tree)
이진 트리는 트리의 한 종류로써, 모든 노드가 최대 두 개의 자식을 가지는 트리이다.
- 모든 노드의 차수가 2 이하다.
- 모든 노드가 2개의 서브 트리를 가지고 있다.
1. 정 이진 트리(Full binary tree)
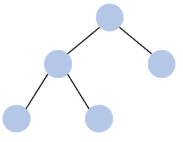
- 모든 노드가 0개 또는 2개의 자식 노드를 가진 이진 트리이다.
- 리프 노드를 제외한 모든 노드의 자식 노드가 2개
2. 포화 이진 트리(Perfect binary tree)
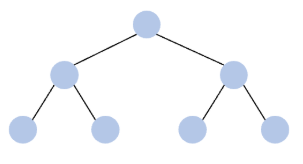
- 트리의 모든 레벨에서 노드가 모드 채워져 있는 이진 트리이다.
3. 완전 이진 트리(Complete binary tree)
- 마지막 레벨을 제외한 모든 레벨에 노드가 완전히 채워져 있고, 마지막 레벨에는 노드가 왼쪽부터 채워져 있는 이진 트리이다.
4. 편향 트리(Skewed tree)
- 리프노드를 제외한 모든 노드가 하나의 자식 노드만 가지는 트리