[백준, JAVA] 2579번 : 계단 오르기

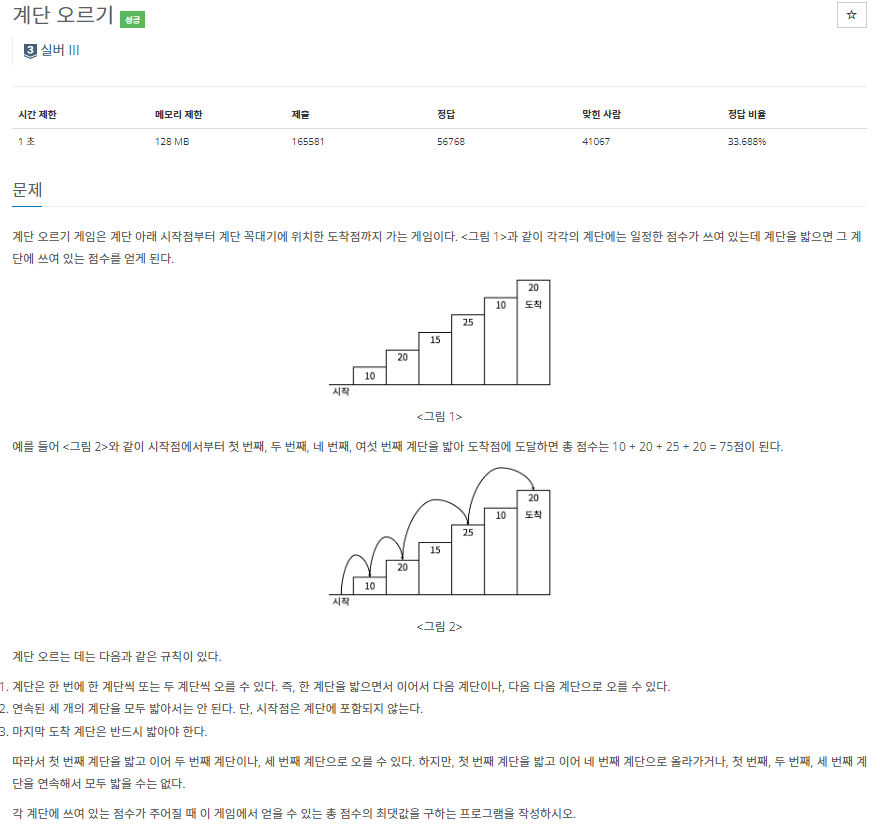
1. 문제

2. 아이디어

• 제약조건
  1) 마지막 계단은 무조건 밟아야 한다.
  2) 세 계단을 연속으로 밟을 수 없다.
  3) 계단은 1칸 혹은 2칸 씩 올라갈 수 있다.
  ++ 당연하게도 계단의 순서가 중요하니, 정렬을 하면 안된다 ㅎㅎ;

• 2)와 3)번 조건을 고려하며 몇가지 생각을 하다가 다이나믹 프로그래밍 개념 이해가 더욱 생겼다.
  (문제를 쪼개어 작은 문제부터 해결한다는게 무슨 뜻인지 알겠다는?)
  아래는 사고의 흐름이다..!

1. 마지막 계단을 밟기 위해서는 D-F (2칸) 혹은 E-F(1칸)이다. D-E-F는 불가능하다.

2. "다음 계단을 몇 칸 올라가는 것이 이득인지"를 경우의 수 나열(도착지까지 가보기) 없이 판단할 수 있나? : 불가능하다. 다음 계단에 대한 의사결정은 그 이후에 나오는 계단을 고려해야 한다.

ex) " 현 위치 / 10 / 20 " 상황이라고 가정해보자.

당연히 두 칸을 올라가서 20에 도착 하는 것이 이득으로 보인다.

하지만 알고보니 계단의 점수가 현위치 / 10 / 20 / 100 / 1,000이었다면?

난 이미 20까지 올라왔기 때문에 "현 위치 - 20 - 1000"이 최고 득점이다. (총합 1,020)
(100으로 가면 1,000을 얻지 못한다!)

하지만 "현 위치 - 10 - 100 - 1,000"이 더 좋은 경우의 수 이다. (총합 1,110)

해당 예시에서도, 이후에 오는 숫자의 절댓값과 순서에 따라 경로의 최선은 달라질 것이다.

이렇듯 이후의 숫자를 의사결정에 참고하지 않으면(경우의 수를 모두 나열해보지 않으면) 다음 계단을 몇 칸 가는 것이 이득인지 판단할 수 없다.

• 다음 계단을 예측할 수는 없지만, 현재 위치까지 오는 경로의 최선은 알 수 있다!

• 현 위치를 일종의 "도착지"라고 생각하고, 각각의 출발지~현위치(작은 단위의 문제)까지 오는 제일 좋은 값을 저장(Memoization)하고 활용한다.

"다음 (미래) 선택을 무엇으로 하느냐" 관점이 아니라, "현재 상태에 도달하기까지 과거의 경우" 중, 최선을 찾는다.

• 나름대로 정리한 DP 문제의 접근 방식이다. 타인에게는 전달이 잘 안될 수도 있고.. 엄밀하지 않을 수도 있지만, 굵은 글씨의 부분이 흔히 말하는 "작은 문제"라고 생각하면 될 것 같다.

3. 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
 
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
 
		int N = Integer.parseInt(br.readLine());
 
		int[] dp = new int[N + 1];
		int[] arr = new int[N + 1];
 
 
		for (int i = 1; i <= N; i++) {
			arr[i] = Integer.parseInt(br.readLine());
		}
 
		// index = 0 은 시작점
		dp[1] = arr[1];
		
		if (N >= 2) {
			dp[2] = arr[1] + arr[2];
		}
 
		
		for (int i = 3; i <= N; i++) {
			dp[i] = Math.max(dp[i - 2] , dp[i - 3] + arr[i - 1]) + arr[i];
		}
 
		System.out.println(dp[N]);
 
	}
 
}

4. 느낀점

• "가장 긴 감소하는 부분수열" 문제 풀 때보다 DP 개념 및 활용에 대한 이해가 생겼다.
  https://velog.io/@dev_su_noh/백준-JAVA-11722번-가장-긴-감소하는-부분수열

• 평소에 문제를 접근하는 방식과는 관점이 달라서 재미있었다!