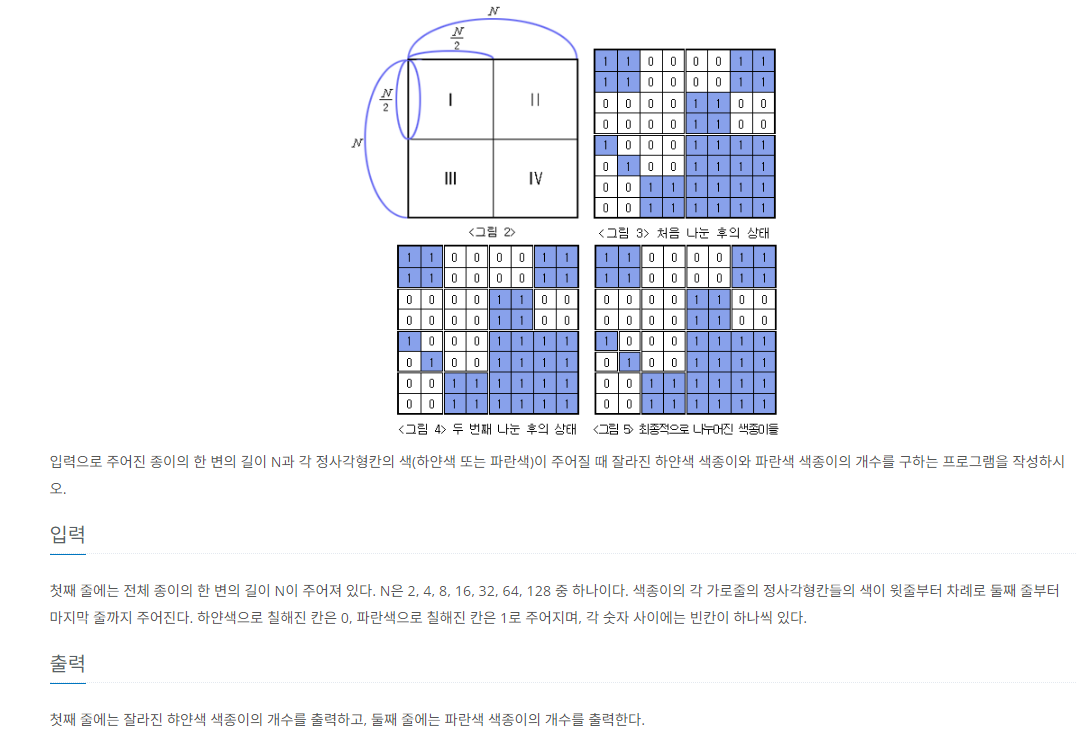
1. 문제

2. 아이디어
* 분할 정복 알고리즘
① 큰 문제를 작은 문제로 분할하고 (Divide)
② 해당 작은 문제들을 풀고(Conquer)
③ 작은 문제들의 풀이 결과를 합한다.
- 음.. 복잡한 아이디어는 아니기 때문에 무슨 말인지는 알겠다.
근데 위의 내용만으로는 추상적이라 실제 코드 작성은 어렵다.
조금 더 구체화해서 생각해보았다!
1) 큰 문제를 가장 작은 단위의 문제까지 쪼개야 한다 -> 재귀호출
2) 어디까지 쪼갤지 알아야 한다 -> 가장 작은 문제 단위를 파악 할 수 있어야 한다.
위의의 두가지 아이디어로 문제를 접근해보자.
- 분할 정복 관련해서 몇가지 문제를 풀어보았는데, 문제 상황이 대부분 2차원 배열이었다.
아마 문제를 처음 보면 DFS/BFS인가?라는 생각을 먼저 할 것 같다.
- 그렇다면, 분할 정복임을 어떻게 캐치할 수 있을까?
차이점? 특징?을 나름대로 생각해보았다. 정리하고 보니 꽤나 차이가 나는 것 같다.
1) 특정 행위를 계속해서 반복한다. (한 칸 씩 이동하면서 경로를 탐색하는 관점이 아님)
2) 1번에서의 반복 행위는 보통 나눗셈이 진행된다.
-> 대부분의 입력 값이나 조건이 지수 형태를 띄고 있다. (나누어 떨어지도록)
3. 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static int[][] map;
public static int white;
public static int blue;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(bf.readLine());
map = new int[N][N];
StringTokenizer st;
for (int i = 0; i < N; i++) {
st = new StringTokenizer(bf.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
divide(0, 0, N);
System.out.println(white);
System.out.println(blue);
}
public static void divide(int row, int col, int size) {
if(colorCheck(row, col, size)) {
if(map[row][col]==0) white++;
else blue++;
return;
}
int newSize = size/2;
divide(row, col, newSize); // 2사분면
divide(row, col+newSize, newSize); // 1사분면
divide(row+newSize, col, newSize); // 3사분면
divide(row+newSize, col+newSize, newSize); // 4사분면
}
public static boolean colorCheck(int row, int col, int size) {
int color = map[row][col]; // 시작점(원점)의 색
for(int i=row; i<row+size; i++) {
for (int j = col; j < col+size; j++) {
if(map[i][j]!=color) return false; // 시작점의 색이 무엇이든, 같지 않다면 false
}
}
return true;
}
}4. 느낀점
-
여러 알고리즘을 공부하다 보니, 이제는 받아들이는 속도가 좀 빨라졌다.
-
재귀호출의 개념과 활용을 잘 할 수 있다면 어렵지 않게 풀 수 있는 개념 같다.
