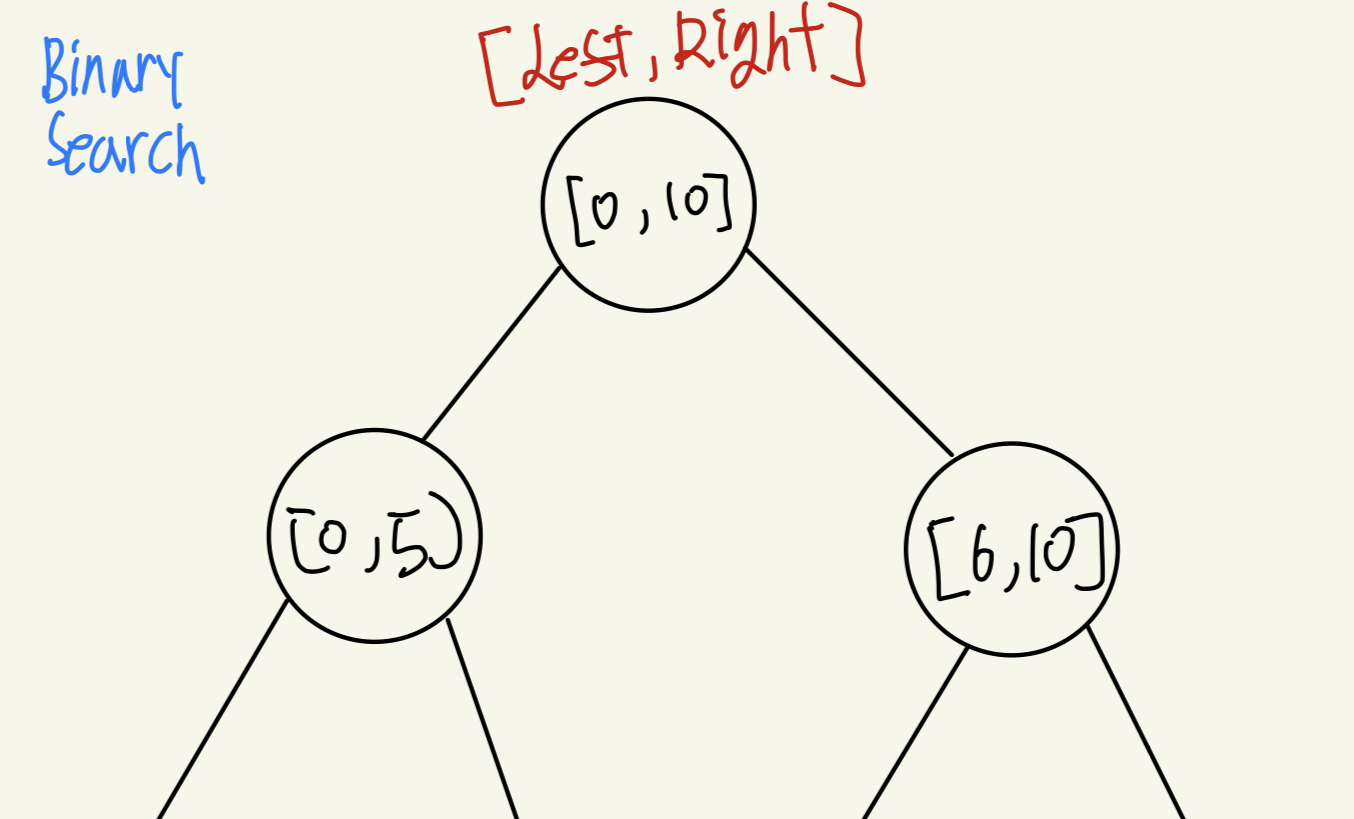
0. 개요
Binary Search 는 정렬 되어있는 배열에서 우리가 원하는 값 혹은 Lower Bound, Upper Bound 를 O(log(N)) 의 시간 복잡도로 찾을 수 있게 해주는 알고리즘이다.
알고리즘 자체는 이해하기 어렵지 않지만, Binary Search 의 범위를 어떻게 설정할 지, 탐색 범위를 조정하는 조건문은 어떻게 설정할지 등에 대해 제대로 정형화가 되어있지 않아 문제들을 감(?) 으로 푼다는 느낌이 들어, 나만의 방식으로 정형화를 시켜보고자 한다.
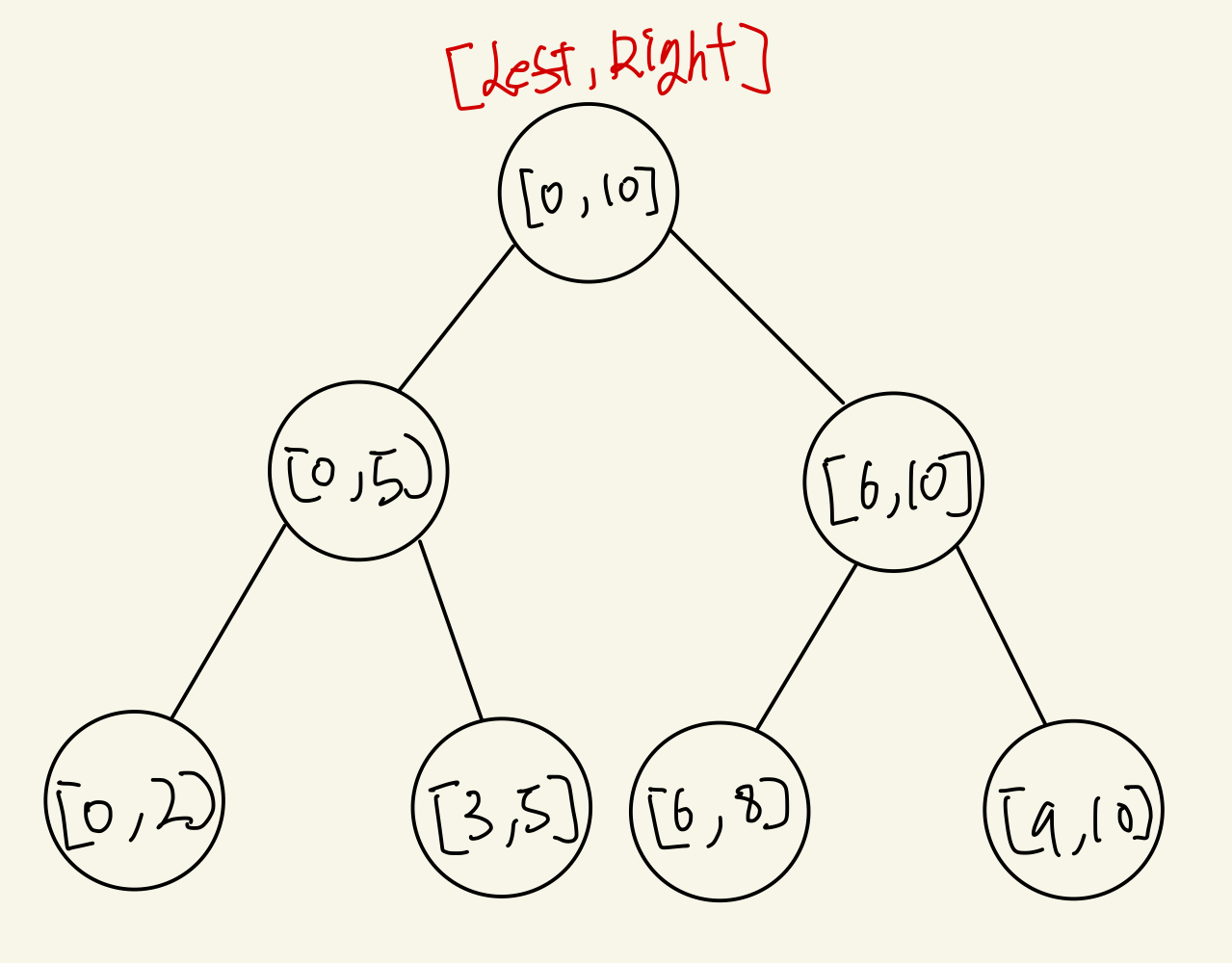
I. while 조건문 & 범위 갱신 조건 설정
Binary Search 의 while 조건문은 left <= right, left < right, left + 1 < right 와 같이 크게 세가지 유형으로 구현되는 것 같다. 이는 Binary Search 의 반복문 조건식에 따라 달라지는데, 이에 대해 아래 두 코드를 비교해 보자.
// left <= right while loop
int left = beg, right = end;
while(left <= right) {
mid = (left + right) / 2;
if(chk(mid))
left = mid + 1;
else
right = mid - 1;
}left = mid + 1, right = mid - 1 식으로 탐색 범위를 갱신한다.
이는 범위 갱신시 left 혹은 right 의 값을 탐색 범위에서 제거함을 의미하며, left == right 범위로 갱신될 때 발생하는 무한 루프를 방지한다.
// left < right while loop
int left = beg, right = end;
while(left < right) {
mid = (left + right) / 2;
if(chk(mid))
left = mid + 1;
else
right = mid;
}left = mid + 1, right = mid 식으로 탐색 범위를 갱신한다.
이는 범위 갱신시 right 의 값을 탐색 범위에서 제거함을 의미하며, ⌊(mid + 1 + right) / 2⌋ == (mid + right) / 2 일 때 발생하는 무한 루프를 방지한다.
// left + 1< right while loop
int left = beg, right = end;
while(left + 1 < right) {
mid = (left + right) / 2;
if(chk(mid))
left = mid;
else
right = mid;
}left = mid, right = mid 식으로 탐색 범위를 갱신한다.
이는 범위 갱신 시에 left 와 right 를 다음 탐색 범위에 포함하는 것을 의미하며, left 와 right 사이에 하나 이상의 원소가 존재한다.
이 경우, 주로 mid 가 정답으로 출력되는 위의 두 경우와 달리 정답을 위한 조건식을 만족하는 마지막 값인 left 혹은 right 가 정답으로 출력되는 경우가 많다.
추가적으로, 초기 탐색 범위에 대해서는, mid 의 갱신이 mid == ⌊(left + right) / 2⌋ 의 특성을 가지기에, 오른쪽을 열린 범위([beg, end))로 설정하는 편이 많은 것 같다.
II. 범위 갱신 시 주의해야할 점
위에서 언급했듯이, 갱신 시에 left 혹은 right 를 다음 탐색 범위에서 제외시키는 경우가 있는데, 만약 left 혹은 right 가 정답을 포함하고 있을 때, 탐색 범위에서 제외되는 경우에 대해 주의하여야 한다. 이에대해, 아래 문제의 코드를 예시로 설명하겠다.
//BOJ - #1300
cin >> N >> K;
int ans = 0;
ll left = 1, right = N * N + 1, mid;
while(left < right) {
mid = (left + right) / 2;
ll cnt = 0;
for(ll row = 1; row <= N; ++row)
cnt += min(N, (mid - 1) / row);
if(cnt < K) {
ans = mid;
left = mid + 1;
}
else
right = mid;
}
cout << ans;위의 코드에서, left 를 mid + 1 로 갱신하는 조건은 NxN 배열 A 의 값들 중, mid 보다 작은 값들의 수가 K 보다 작을 때 이다.
그런데, mid 가 정답일 때 역시 mid 보다 작은 값들의 수가 K 보다 작은데, 이 때문에 mid 가 정답임에도 조건식에 따라 mid 를 탐색 범위에서 제거해 버리게 된다.
따라서, 이러한 경우엔 정답과 동일한 조건식을 가지는 갱신에 대해서 mid 값을 다음 탐색 범위에서 제외시키지 않는 방식을 사용하거나, 위의 코드와 같이 별도의 변수를 사용해 정답을 수시로 저장해 주는 방식을 사용해야 한다.
III. 여담
Binary Search 는 순차적 배열, O(log(n)), 원하는 값 찾기, 이 세가지 요소를 잘 찾아내는 직관이 그 무엇보다 중요한 것 같다.
그래도 Dynamic Programming 과 같이 부분 문제를 정의해 봐야한다거나 하는 과정은 없어 다른 알고리즘들에 비하면 직관을 얻기는 상대적으로 쉬운 것 같다.
