[ 글또 7기 ] 반올림이 뭐라고 생각하세요?

이주 weekwith.me·2022년 6월 12일

목록 보기

2/4

블로그를 이전 중이라 완료되기 전까지는 벨로그에 작성할 계획입니다.
이후 모든 글은 https://weekwith.me 에 작성 예정이니 다른 글이 궁금하시다면 해당 링크를 통해 방문해주세요.

본 제목은 유튜버 침착맨 -만화가 이말년- 님이 본인의 침착맨 플러스 채널에 2022년 3월 27일 업로드한 영상 재즈를 뭐라고 생각하세요?를 응용했습니다.

도입

아래 Python 코드의 결괏값을 한번 생각해보자. True 가 나올까 False 가 나올까?

print(round(1.5) == round(2.5)) # > True or False?

눈치 빠른 사람들은 물어본 이유를 이미 알아챘을 것이다. 정답은 True 다.

우리가 학창시절 배운 반올림(Round)은 숫자 5를 기준으로 이상이면 올림, 미만이면 내림이라 배웠는데 왜 이럴까?

Python 작동 원리

우선 Python 공식문서를 한번 살펴보자.

Python 내장 함수인 round() 함수에 대해서는 아래와 같이 설명되어 있다.

round() 함수는 기본적으로 값을 10의 가장 가까운 n의 배수로 반올림하며 이때 두 배수가 동일하게 근접하다면 짝수를 선택한다. (따라서, 예를 들어, round(0.5) 와 round(-0.5) 의 결괏값은 0 이고, round(1.5) 의 결괏값은 2 다.)

For the built-in types supporting round() , values are rounded to the closest multiple of 10 to the power minus ndigits; if two multiples are equally close, rounding is done toward the even choice (so, for example, both round(0.5) and round(-0.5) are 0 , and round(1.5) is 2 ).

중요한 점은 짝수를 선택한다는 부분이다. 그리고 이러한 작동 방식에 대해서는 아래와 같이 서술되어 있다.

실수형(float)에 대한 round() 함수의 작동 방식은 예상과 다를 수 있다. 예를 들어 round(2.675, 2) 는 그 결괏값으로 2.68 대신 2.67 을 반환한다. 이것은 버그가 아닌 대부분의 소수가 부동 소수점 -실수형(float)- 을 정확히 표현할 수 없다는 사실에 기인한다.

The behavior of round() for floats can be surprising; for example, round(2.675, 2) gives 2.67 instead of the expected 2.68 . This is not a bug: it's a result of the fact that most decimal fractions can't be represented exactly as a float.

결과적으로 실수형에 대해 Python 내장 함수 round() 를 사용할 경우 기본적으로 짝수를 선택해서 결괏값을 반환한다는 의미다. 그리고 이는 소수가 부동 소수점을 정확히 표현할 수 없기 때문이다.

위 영어 표현에서 decimal fractions 라는 표현을 소수라 번역했다. 여기서 decimal 은 10진수를, fractions 는 분수를 의미한다. 따라서 소수는 다시 말해 4/9 와 같이 우리가 흔히 사용하는 10진수로 표현된 분수라 생각하면 된다. 그런데 이 분수는 결국 소수로도 - 예를 들어 1/2 는 0.5 - 나타낼 수 있다. 다시 말해 우리가 흔히 생각하는 그 소수 표현이 부동 소수점으로 표현될 때 정확하게 표현되지 못한다는 것이다.

그렇다면 어째서 정확하게 표현할 수 없다는 걸까?

컴퓨터의 수 표현

컴퓨터는 기본적으로 이진수(Binary)로 모든 작업을 한다. 이는 곧 회로와도 연결된 것으로 전구에 불이 켜졌을 때 1 - True -, 불이 꺼졌을 때 0 - False - 으로 작동하여 모든 수부터 문자열, 함수와 애플리케이션까지 작동시킨다. 예를 들어 A 라는 문자 또한 아스키 코드(ASCII Code)에 의해 대응되는 10진수 숫자인 65 , 그리고 이는 2진수로 곧 01000001 로 변환되어 컴퓨터는 해석한다. 컴퓨터는 결국 0 과 1 밖에 이해하지 못한다는 의미다.

이는 정수를 표현할 때는 크게 문제가 되지 않는다. 자연수의 경우 위 예시처럼 - 십진수 65 를 이진수 01000001 로 변환한 것처럼- 이진수로 간편하게 변환할 수 있다. 음수 또한 크게 문제가 되지 않는다. 2의 보수(Complement)라는 개념을 사용하여 2진수의 숫자 0 은 1 로, 1 은 0 으로 바꾼 다음 1 을 더해준다. 이때 2의 보수는 결국 1의 보수에 1 을 더하는 방식과 똑같다. 예를 들면 아래 이미지와 같다. 결국 절대값이 똑같은 양수와 음수는 더했을 때 0이 되어야 한다.

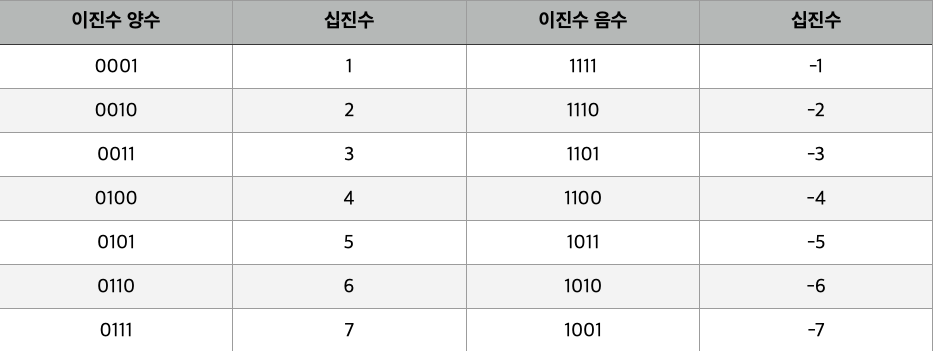
여기서 보수는 쉽게 보충해주는 수를 의미한다.

다시 말해 이진수의 1의 보수는 결국 이진수에 어떤 수를 더해 1 을 만들어야 한다는 의미이기 때문에 0 과 1 밖에 존재하지 않는 이진수에서는 0 을 1 로 바꾸고 1 을 0 으로 바꿔 더하면 두 수의 합이 1 이 된다.

그러나 문제는 소수를, 다시 말해 실수형을 표현할 때 발생한다.

소수 표현

10을 곱하거나 나누어서 앞서 살펴본 소수를 표현할 수 있듯, 이진수 또한 2를 곱하거나 나누어서 소수점을 표현할 수 있다. 그리고 이런 원리를 활용하여 이진수에서도 소수를 표현하는 방식이 바로 부동 소수점(Floating-Point)다. 예를 들어 101.11 이라는 이진수의 수가 존재하면 이를 1.0111 * 2^3 과 같은 방식으로 표현할 수 있다. 142.65 이라는 십진수를 1.4265 * 10^2 으로 표현할 수 있는 것과 똑같다.

부동 소수점이 아닌 고정 소수점(Fixed Point) 방식 또한 존재한다. 두 차이에 관해서는 자세하게 언급하지 않겠다.

부동 소수점은 소수를 표현할 때 양수와 음수를 구분할 수 있는 부호부, 부호있는 정수를 표현하는 지수부, 그리고 실제값을 저장하는 가수부로 나누어 표현한다. 이때 앞선 예시와 같이 1 로 시작하여 그 뒤에 .0111 * 2^3 과 같은 형태로 표현하는데 이를 정규화(Nomorlization)라고 한다. 1.0111 * 2^3 의 경우 앞의 1 이 곧 부호 부분이고 -부호있는 정수가 따로 존재하지 않기 때문에- 뒤 0.111 이 가수가 된다.

그런데 파이(3.14)처럼 무한소수가 존재하기도 하고 십진수를 실제 이진수로 변환할 때 무한소수가 되는 경우도 있다. 예를 들어 소수 1/3 은 이진수로 변환하면 0.00011001100110011001100 ... 과 같이 무한히 뒤가 이어진다. 그리고 부동 소수점을 표현하는 과정에는 컴퓨터의 물리적 한계로 메모리의 한계가 존재할 수밖에 없다. 예를 들어 Java의 경우 float 자료형은 4바이트(Byte)가 할당되어 부호에 1비트, 지수에 8비트, 나머지 가수에 23비트를 저장하고 double 자료형은 8바이트가 할당되어 똑같이 부호에 1비트, 지수는 11비트, 가수에는 52비트까지 저장 가능하다.

결국 이진수로 모든 것을 작동시키는 컴퓨터의 한계로 인해 소수를 표현할 때 부동 소수점 방식을 사용하게 되었고 이 과정에서 메모리의 한계 등으로 인해 오차가 발생하는 것이다. 그리고 이는 곧 아까 살펴보았던 소수를 부동 소수점으로 정확하게 표현할 수 없기 때문에 Python round() 함수의 작동 방식을 흔히 아는 것과 달리 가까운 짝수로 변환한다는 것이다.

IEEE 754의 권장

Python2까지는 사실 이러한 방식과 달리 흔히 알고 있는 반올림과 동일한 방식으로 작동했다. 그런데 국제 전기전자공학자협회(Institute of Electrical and Electronics Engineers)가 발표한 표준 부동 소수점 연산 문서인 IEEE 754: Standard for Floating-Point Arithmetic에서 권장한 방식을 따르게 되었다.

다른 방법

물론 Python에도 다른 반올림 방식을 사용할 수 있는 방법이 있다. 바로 decimal 내장 모듈을 사용하는 것이다. 예를 들어 아래와 같이 반올림 방식을 getcontext() 함수를 통해 ROUND_HALF_UP 으로 바꿔줄 수 있다. 그러면 결과적으로 십진수 2.5 의 반올림 결괏값이 3 이 되어 맨 처음 봤던 round(1.5) == round(2.5) 의 출력 결과물과 달리 False 를 반환하는 걸 확인할 수 있다.

import decimal
from decimal import Decimal


decimal.getcontext().rounding = decimal.ROUND_HALF_UP

first_num = decimal.Decimal("1.5").quantize(decimal.Deciaml("1"))
second_num = decimal.Decimal("2.5").quantize(decimal.Decimal("1"))

print(first_num == second_num) # > False
print(second_num) # > Decimal("3")

decimal 모듈에 관한 더 자세한 내용은 Python 공식 문서 decimal - Decimal fixed point and floating point arithmetic: Rounding modes를 확인하길 추천한다.

반올림의 종류

이러한 수학적 근사값의 오류를 극복하고자 사실 정말 많은 반올림 종류가 있다. 다시 말해 반올림의 대상이 되는 범위를 어떻게 정의할 것인 지에 따라 여러 반올림 방식이 존재한다. 그리고 Python2와 달리 Python3 - 이하 Python - 에서는 IEEE 754 방식을 따른 것처럼 각각의 프로그래밍 언어에 따라 사용하는 방법 또한 다르다.

사사오입(Round Half Up)

대표적으로 알고 있는 반올림 방법으로 산술적 반올림이라고도 한다. 숫자 5를 기준으로 그 이상이면 올림, 미만이면 내림을 한다. 이러한 방식을 사용하는 대표적인 프로그래밍 언어로는 C/C++, Java, JavaScript, Go 등이 있으며 이외에도 Oracle, MySQL 등의 RDBMS 또한 있다.

예를 들어 아래와 같이 Java에서 round 메서드를 사용할 경우 흔히 떠올리는 반올림 방식과 동일한 결괏값인 3 을 반환한다.

public class Example {
	public static void main(String[] args) {
    	System.out.prinln(Math.round(2.5)); // > 3
    }
}

오사오입(Round Half to Even)

앞서 계속 살펴봤던 Python에서 사용하는 방식으로 뱅커스 라운딩(Banker's Rounding)이라고도 한다. 사사오입과 동일하게 똑같이 숫자 5를 기준으로 하는데 이때 5의 앞자리가 홀수인 경우 올림을 하고 짝수인 경우 내림을 한다. 이러한 방식을 사용하는 대표적인 프로그래밍 언어 Python 외에도 Julia, Kotlin 등이 있다.

예를 들어 아래와 같이 Kotlin에서 round 메서드를 사용할 경우 2 를 반환한다.

import kotlin.math.round

fun main(args: Array<String> {
	println(round(2.5) // > 2
}

Java를 Kotlin으로 리팩토링할 때 이러한 경우에 주의해야 한다. 그래서 직접 라이브러리에서 round 메서드를 사용하는 것이 아닌 다른 방식으로 반올림하는 경우가 많다.

이외에도 더 다양한 반올림 방식이 존재하는데 자세한 부분은 맨 아래 참고 문헌 부분 중 위키피디아 부분에서 Rounding 문서를 확인하길 추천한다.

결론

Python에서의 내장 함수round()는 우리가 흔히 생각하는 반올림 방식과는 조금 다르게 작동한다. 이는 부동 소수점을 표현하는 방식에 있어서 오차가 발생하는 부분 때문에 이를 해결하고자 IEEE 754가 권장한 방식을 따른 결과이다. 이때 만약 다른 반올림 방식을 사용하길 원한다면 decimal 내장 모듈을 활용할 수 있다.

여러 프로그래밍 언어 - 더 나아가 RDBMS까지 - 마다 사용하는 반올림 방식이 다르기 때문에 정교한 수치 계산이 필요한 작업을 할 때는 한 번쯤 그 방식에 대해 알아보고 사용해보자. 예를 들어 Java와 Kotlin에서의 방식이 서로 다르기 때문에 Java에서 Kotlin으로 코드를 리팩토링할 때 원하던 결괏값이 아닌 완전히 다른 값을 얻을 수 있기 때문이다.