Java의 참조형 캐스팅
타입 변환(형 변환, Casting)이란? 하나의 데이터 타입을 다른 타입으로 바꾸는 것
자바의 데이터 형
- 기본형(primitive type) - Boolean(boolean), Numeric(short, int, long, float, double, char)
- 참조형(reference type) - Class, Interface, Array, Enum, etc.
→ 타입 간 변환을 캐스팅이라고 했으니, 기본형과 참조형 간에도 변환이 가능한 것이다. ( ) 캐스팅 연산자를 사용하면 강제적으로 타입을 지정하여 변수에 대입할 수 있는데, 업캐스팅과 다운캐스팅은 자바의 상속 관계에 있는 부모-자식 클래스 간의 형 변환에서부터 나온 개념이다.
클래스는 참조형 타입이므로 이를 참조형 캐스팅 (업캐스팅 / 다운캐스팅)이라고 부른다.
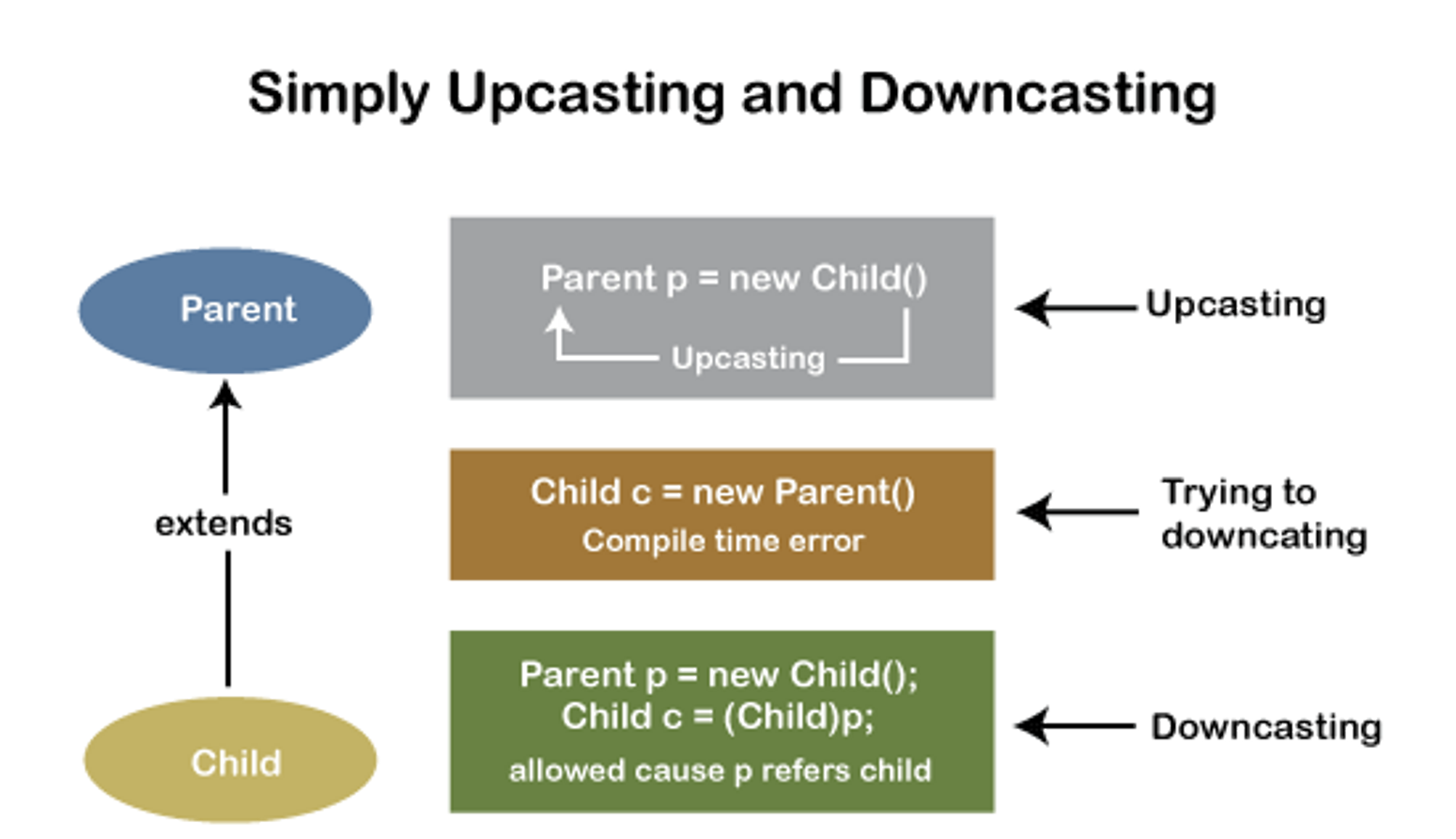
업 캐스팅 : 자식 → 부모 , 다운 캐스팅 : 부모 → 자식
자식 클래스의 객체는 부모 클래스를 상속하므로, 부모의 멤버를 기본적으로 모두 가지고 있다. 하지만, 부모는 자식의 멤버를 가지지 않는다. 참조변수 간의 형 변환을 하는 근본적인 이유는 사용가능한 멤버의 개수를 조절하는 것이다.
대표적으로, List<int> list = new ArrayList<>(); 가 업 캐스팅의 특징을 잘 보여준다. 형제 클래스 끼리는 타입이 아예 다르므로 참조 형변환이 불가능한데, 이와 같이 업 캐스팅을 하면 list는 ArrayList, LinkedList 등 경우에 맞게 지정할 수 있다.
업캐스팅(UpCasting)
자식 클래스가 부모 클래스 타입으로 캐스팅되는 것으로, 캐스팅 연산자 괄호를 생략할 수 있다. 업캐스팅은 멤버 개수의 감소(=멤버 접근 제한)를 의미하며, 이는 자식 클래스에만 있는 멤버를 사용할 수 없음을 의미한다.
업캐스팅을 하고 메소드 실행 시, 자식 클래스에서 오버라이딩한 메서드가 있을 경우에 부모 클래스의 메서드가 아닌 오버라이딩 된 자식 클래스의 메서드가 실행된다. 이는 오버라이딩 특성상 코드가 실행하는 런타임 환경에서 동적으로 바인딩 되었기 떄문이다.
업캐스팅을 하는 이유?
업캐스팅의 목적은 다형성과 연관되어 있다. 업캐스팅을 통해 재사용해야 하는 반복된 메서드를 부모클래스에서 가져와 서브클래스를 호출하는 등 자유롭게 사용이 가능해진다. 예시로, Triangle, Rectangle, Circle 클래스가 있다고 하자. 이를 Shape이라는 하나의 자료형으로 관리한다면 코드의 양과 가독성 측면에서 훨씬 효율적이게 되고 유지보수에도 좋아진다.
Shape[] s = new Shape[];
s[0] = new Rectangle();
s[1] = new Rectangle();
s[2] = new Triangle();
s[3] = new Triangle();
s[4] = new Circle();
s[5] = new Circle();다운캐스팅(DownCasting)
거꾸로 부모 클래스가 자식 클래스 타입으로 캐스팅되는 것으로, 캐스팅 연산자 괄호를 필수로 적어줘야 한다. 다운캐스팅은 업캐스팅한 객체를 다시 자식 클래스 타입의 객체로 복구하기 위한 목적을 가진다. 즉, 업캐스팅의 반대 개념으로 생각하기 보다 자신이 원래 가지던 기능을 업캐스팅에 의해 잃어버렸다가 다시 회복하기 위해 다운캐스팅을 한다는 개념으로 접근하는 것이 좋다.
다운 캐스팅은 객체 멤버의 증가를 의미하는 것과 같으므로, 이는 매우 불안전하다. 실제 참조변수가 가리키는 객체가 무엇인지 불분명한 상태에서 멤버가 추가되는 것이므로, 반드시 형변환 연산자를 같이 명시해줘야 어떤 클래스의 멤버가 추가되는지 알 수 있다.
주의할 사항
다운캐스팅은 업캐스팅한 객체를 되돌릴 때 적용되는 것이므로, 기존 오리지날의 부모 객체를 자식 객체로 강제 형변환하려고 시도하면
**ClassCastException**이 발생한다.
또한, 형제 클래스 간의 형 변환은 불가능하므로, 다운캐스팅 이후에 형제 클래스 멤버에 접근하면 컴파일 에러, 런타임 에러가 발생할 수 있다.
이처럼 무분별한 다운캐스팅은 컴파일 시점에 오류가 발생하지 않아도 런타임 오류를 발생시킬 가능성이 있으며, 다운캐스팅을 다룰 때 다운캐스팅할 객체가 1. 오리지날 부모 객체인지 2. 업캐스팅된 부모 객체인지 항상 판단해줄 필요가 있다.
instanceof 연산자
참조 캐스팅에서의 오류와 혼동을 방지하기 위해 자바에서 기본 제공해주는 연산자가 바로 instanceof 연산자이다. 어느 객체 변수가 어느 클래스 타입인지를 판별하여 boolean 값을 반환하는 instanceof 는 참조형 객체 변수에만 사용가능하며, 이를 통해 다운캐스팅할 객체에 대한 판별을 해줄 수 있다.
