A Rapid Review of Clustering Algorithms
Abstract
클러스터링 알고리즘은 데이터의 패턴과 유사성을 기반으로 데이터를 그룹으로 나누는 것을 목표로 한다. 현재로서는 모든 작업에 보편적으로 적용할 수 있는 알고리즘이 없다. 기본 원칙 및 특성, 클러스터에 대한 데이터 포인트 할당, 데이터 세트 용량, 미리 정의된 클러스터 번호에 따라 알고리즘을 분류한다. 클러스터링 알고리즘의 현재 추세와 미래 방향에 대해 논의한다.
Introduction
클러스터링 알고리즘은 특정 기준에 따라 유사한 데이터 포인트를 그룹화하여 데이터셋 내의 패턴을 드러내는 머신러닝 알고리즘이다. 주된 목적은 데이터를 하위 그룹으로 나누는 것이다.
- semi-supervised learning: 레이블이 존재하는 데이터와 존재하지 않는 데이터 모두를 훈련에 사용하는 것이다.
ex) Semi-Supervised Fuzzy C-Means - unsupervised learning: 레이블이 존재하지 않는 데이터를 사용한다. 데이터의 패턴과 구조를 식별한 다음 그룹화에 대한 사전 지식 없이 유사성을 기반으로 그룹화한다. 일반적으로 전체 데이터셋의 총 클러스터 수는 알 수 없다.
ex) K-Means, Density-Based Spatial Clustering of Applications with Noise(DBSCAN), Fuzzy C-Means(FCM)
최적의 k를 찾기 위해 사용되는 방법으로는 elbow method, silhouette score, gap statistics가 있다.
Method
'클러스터링', '클러스터링 알고리즘', '클러스터링 방법', '합의 클러스터링', '클러스터링 기술'과 같이 주제와 관련된 키워드로 논문을 검색했다. 실험 설계, 표본 크기, 통계적 방법론과 같은 측면을 고려하여 결과의 신뢰성을 평가하고, 패턴과 추세를 종합했다.
Results
클러스터링 알고리즘을 분류하여, 사용자가 특정 클러스터링 작업에 따라 적합한 알고리즘을 선택하도록 안내하는 것을 목표로 한다.
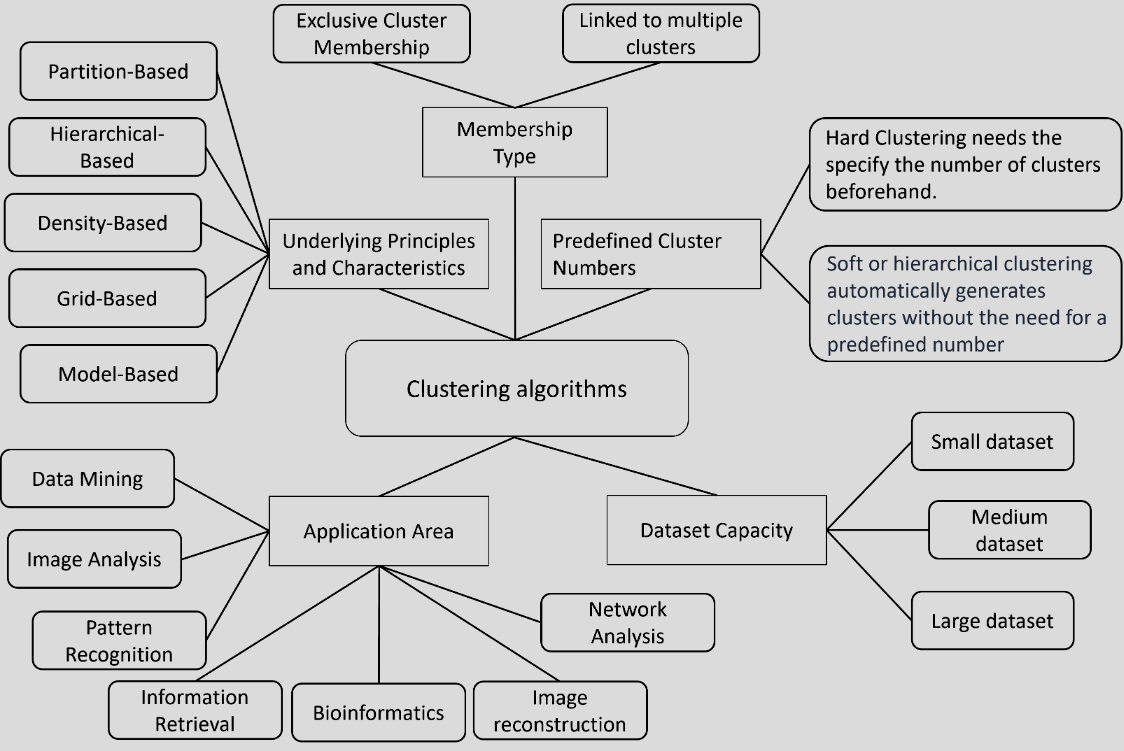
Algorithm Classification by Underlying Principles and Characteristics
기본적 특성 및 접근 방식에 따라 다섯가지 하위 집합으로 그룹화된다.
-
Partition-Based Clustering: 데이터를 겹치지 않는 클러스터로 분할한다. 데이터 포인트의 중심을 해당 클러스터의 중심으로 간주한다. 볼록하지 않은 데이터에는 적합하지 않고 outlier에 민감하며 local optima에 쉽게 포함될 수 있다. 미리 정의된 수의 클러스터가 필요하여 클러스터링 결과의 성능에 영향을 미칠 수 있다.
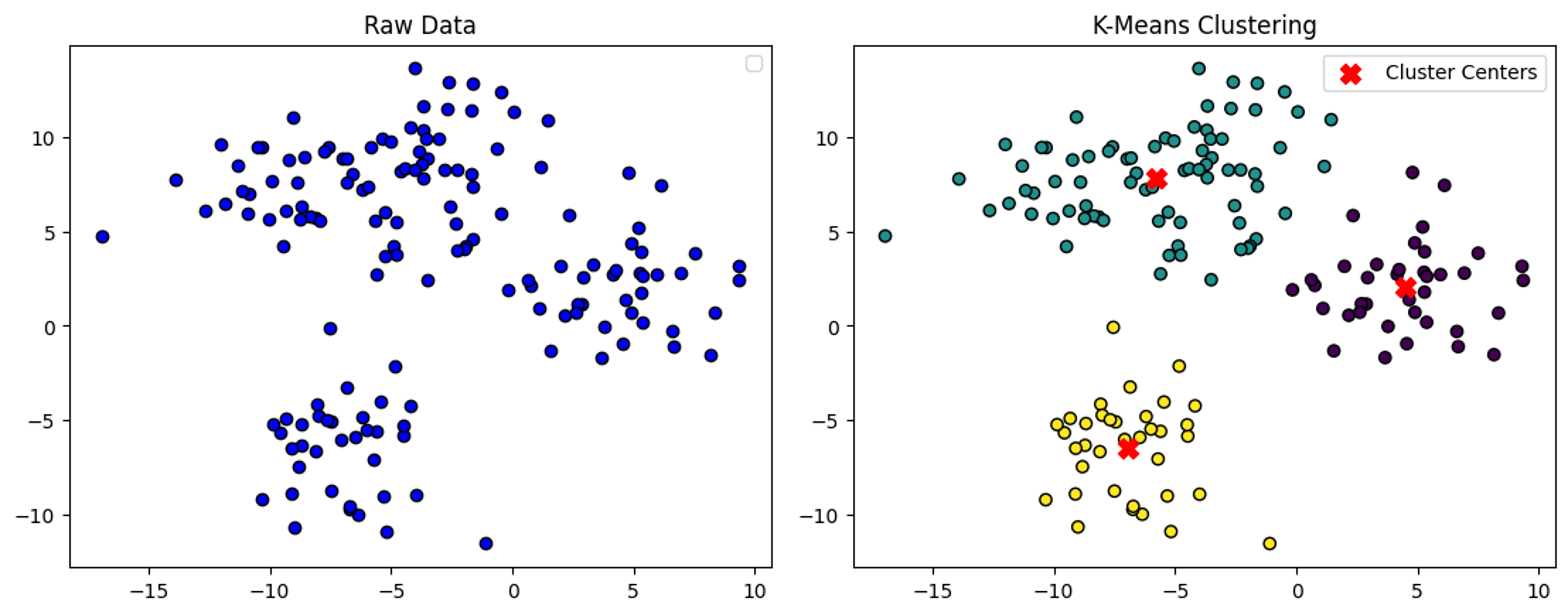
왼쪽 사진은 원래 데이터를 나타낸다. 오른쪽 사진은 K-Means 클러스터링 알고리즘을 적용한 후의 결과를 보여준다. -
Hierarchical-Based Clustering: dendrogram은 모든 데이터 포인트 간의 관계를 포함하는 트리와 같은 구조이다. 미리 클러스터의 수를 정의할 필요가 없다. 시간 복잡도는 높으며, 노이즈와 outlier에 민감하여 최적이 아닌 클러스터가 생성될 수 있다.
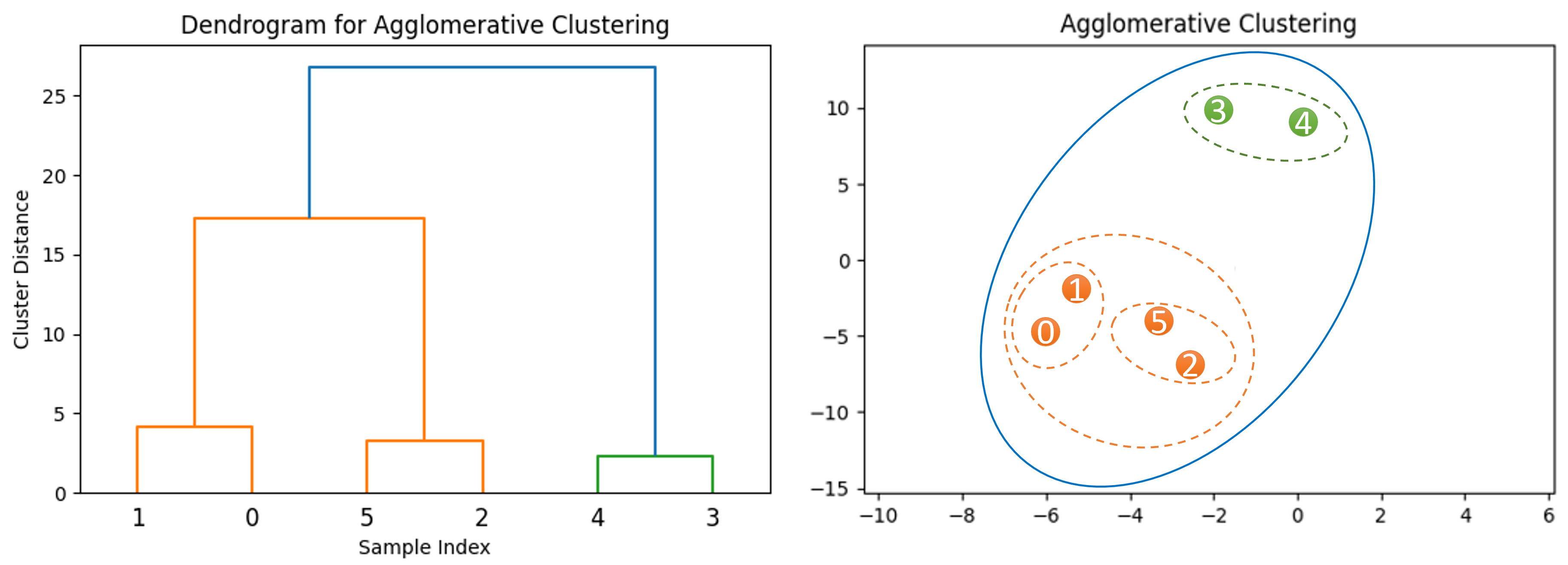
왼쪽 사진은 데이터셋의 샘플 간의 관계를 통해 구성된 dendrogram이다. 오른쪽 사진은 dendrogram을 기반으로 생성된 클러스터를 보여준다. -
Density-Based Clustering: 고차원 영역에서 클러스터를 식별하는 동시에 노이즈 포인트를 outlier로 감지하는 것을 목표로 한다. 클러스터링 효율성이 높고 매개변수에 민감하여 임의 모양의 데이터셋에 적합하다. 공간 데이터 밀도가 고르지 않으면 클러스터링 결과의 품질이 떨어진다.
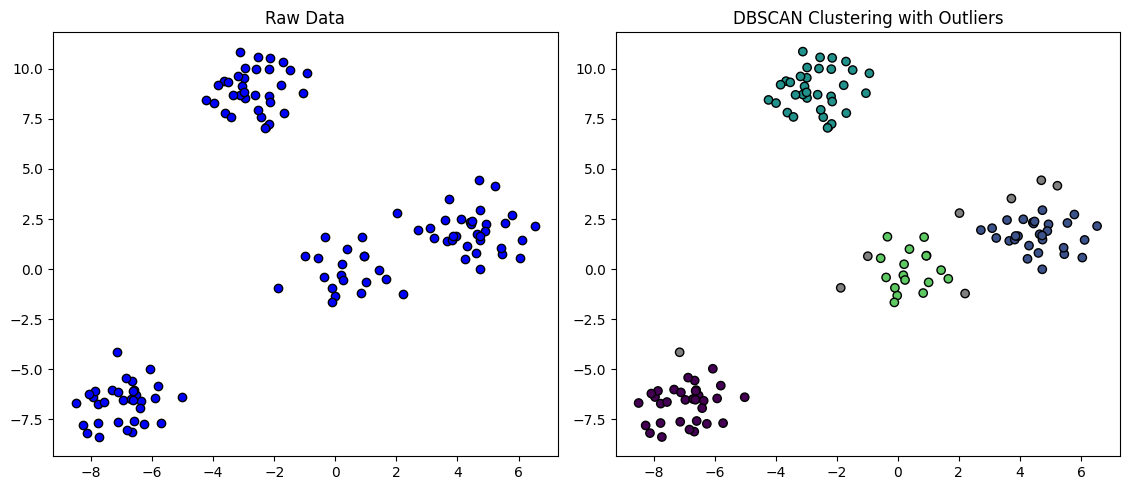
왼쪽 사진은 원래 데이터를 나타낸다. 오른쪽 사진은 알고리즘을 적용한 후의 클러스터링 결과를 보여준다. 회색점이 이상치를 나타낸 것이다. -
Grid-Based Clustering: 초기 데이터 공간을 미리 결정된 크기의 그리드 구조로 분할하는 것이다. 결과가 그리드 크기에 민감하게 작용하며, 계산 효율성을 높이려면 클러스터 품질과 정확도가 낮아진다.
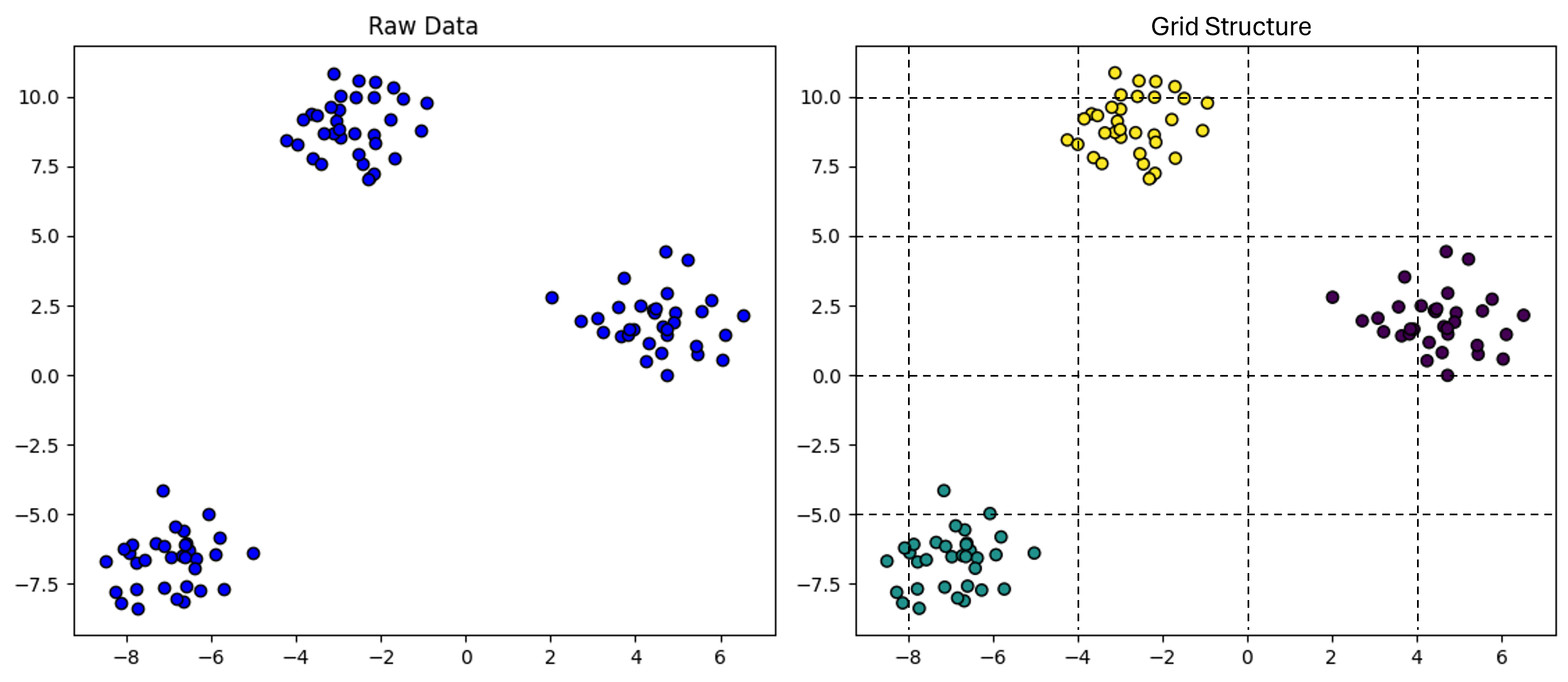
왼쪽 사진은 원래 데이터를 나타낸다. 오른쪽 사진은 그리드 알고리즘 다이어그램이다. -
Model-Based Clustering: 각 클러스터에 대해 특정 모델을 선택하고 해당 모델에 가장 적합한 모델을 찾는 것이다. 데이터 포인트가 확률적 모델에서 생성되었다고 가정하고 데이터 분포를 설명하는데 가장 적합한 모델을 식별한다. 모델의 시간 복잡도는 높고 클러스터링 결과는 선택한 모델의 매개변수에 따라 달라진다.
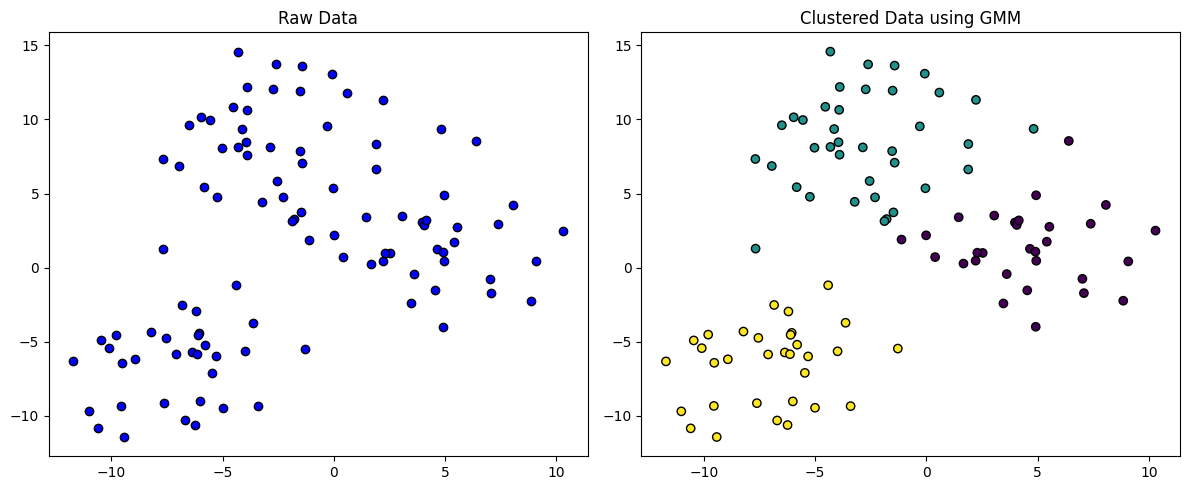
왼쪽 사진은 원래 데이터를 나타낸다. 오른쪽 사진은 Gaussian Mixture Model(GMM)을 적용한 후의 클러스터링 결과이다.
| Category | Benefits | Limitations | Algorithm Examples |
|---|---|---|---|
| Partition-Based Clustering | low time complexity | sensitive to outliers, requires predefined number of clusters | K-Means, K-medoids, PAM, CLARA, CLARANS, FCM |
| Hierarchical Clustering | does not require a predefined number of clusters | high time complexity, denndrogram structure sensitive to noise and outliers | Agglomerative clustering, Chameleon BIRCH, CURE Complete Linkage |
| Density-Based Clustering | high clustering efficiency, suitable for arbitrary cluster shapes | decreased clustering quality for uneven spatial data density, inefficient for large datasets | DBSCAN, DENCLUE, HDBSCAN, Mean-Shift Clustering |
| Grid-Based Clustering | low time complexity, suitable for arbitrary cluster shapes | clusters sensitive to grid size | STDBSCAN, Grid-DBSCAN, WaveCluster |
| Model-Based Clustering | allows for non-spherical clusters, does not require a predefined number of clusters | high time complexity | GMM, HIdden Markov Models(HMM), Latent Dirichlet Allocation(LDA) |
Algorithm Classification by Data Point Assignment to Clusters: Single vs Multi
클러스터링 알고리즘은 데이터 포인트를 클러스터에 할당하는 방식에 따라 분류한다. 크게 두 가지로 나뉘는데, 각 데이터 포인트가 single cluster와 독점적으로 연관되는 hard clustering과 데이터 포인트가 multi cluster와 동시에 연관될 수 있는 soft clustering으로 나뉜다.
- Hard Clustering: K-Means, hierarchical clustering, DBSCAN, OPTICS, K-Medoids 등
- Soft Clustering: FCM, GMM 등
Algorithm Classified by Dataset Capacity
| Dataset | Algorithm Examples | Comments |
|---|---|---|
| Small (~수천) | K-Means, DBSCAN, Hierarchical clustering | 계산 리소스가 적음 |
| Medium (수천~수십만) | Optimized K-Means, GMM, Mean-Shift clustering | - |
| Large (수십만~) | Mini-Batch K-Means, DBSCAN, Hierarchical clustering | - |
Algorithm Classification by Predefined Cluster Numbers
모든 클러스터링 알고리즘에 미리 정의된 수의 클러스터가 필요한 것은 아니다.
- Hard Clustering: 사용자가 미리 클러스터 수를 지정해야 한다. ex) K-Means
- Soft Clustering, Hierarchical Clustering: 클러스터 수를 미리 지정할 필요가 없다. ex) GMM
Hard Clustering은 최적의 클러스터 수를 결정하는 것이 중요하다.
- Elblow Method: SSE(sum of squared error)는 클러스터 내의 데이터 포인트와 해당 클러스터의 중심 간의 거리를 측정한 후 제곱하여 모든 클러스터에 대한 제곱 오차를 합산한 값이다. SSE의 감소율이 급격히 줄어드는 지점이 최적의 k 값이다.
- Silhouette Score: 실루엣 점수는 객체가 다른 클러스터와 비교하여 자체 클러스터와 얼마나 유사한지 측정하는 방법이다. 점수를 최대화하는 지점이 최적의 k 값이다.
- Gap Statistics: 데이터셋의 클러스터링 성능을 임의 데이터셋(또는 더 적은 클러스터)의 성능과 비교한다. 최적의 k 값은 임의 클러스터링에 비해 성능 차이가 커야 한다.
- Dendrogram in Hierarchical Clustering: 계층적 클러스터링 알고리즘에 적용되는 경우 덴드로그램을 시각화하면 적절한 수의 k를 찾을 수 있다.
Algorithm Classification by Area of Application
| Area of Application | Algorithm Examples |
|---|---|
| Data Mining | K-Means, DBSCAN |
| Image Analysis | Spectral Clustering, Mean Shift |
| Pattern Recognition | Hierarchical Clustering, K-Means |
| Information Retrieval | Hierarchical Clustering, K-Means, DBSCAN |
| Bioinformatics | Hierarchical Clustering, Spectral Clustering |
| Image reconstruction | K-Means, Superpixel, Expectation Maximization |
| Network Analysis | Hierarchical Clustering, K-Means, DBSCAN |
Evaluation Metrics
클러스터링 알고리즘은 정답 레이블은 없지만 클러스터링 품질을 평가하는 방법은 있다. 데이터 샘플은 클러스터링 과중 중에 고차원 공간의 벡터로 변환된다. 포인트 간 거리는 클러스터를 형성하는데 중요하며 클러스터링 성능을 평가하는데 사용된다. 일반적인 지표에는 Eucllidean distance, Manhattan distance, 텍스트 데이터의 cosine similarity가 있다. 또한 평가 지표는 internal과 external로 나뉜다.
Internal Evaluation Metrics
데이터의 내재적 특성과 클러스터링 알고리즘의 결과에만 기반하여 클러스터의 품질을 평가할 수 있다. 밀집도, 분산과 같은 클러스터링 품질의 다양한 측면을 측정할 수 있다.
Silhouette Score
가장 널리 사용되는 internal evaluation metric이다. 클러스터가 얼마나 잘 분리되어 있는지 측정한다. single 데이터 포인트에 대한 실루엣 점수는 데이터 포인트에서 같은 클러스터의 다른 포인트까지의 평균 거리(a)와 데이터 포인트에서 가장 가까운 이웃 클러스터의 포인트까지의 평균 거리(b)의 차이를 a와 b의 최대값으로 나누어 계산한다.
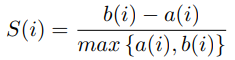
실루엣 점수는 -1에서 1까지이며, 값이 높을수록 더 잘 정의된 클러스터를 나타낸다. 1에 가까운 점수는 데이터 포인트가 자체 클러스터와 잘 일치하고 이웃 클러스터와는 잘 일치하지 않아 좋은 클러스터링을 의미한다. 0에 가까운 실루엣 점수는 겹치는 클러스터를 나타낸다. -1에 가까운 실루엣 점수는 데이터 포인트가 잘못된 클러스터에 할당되었을 수 있음을 나타낸다. 전체 실루엣 점수는 모든 데이터 포인트의 실루엣 점수의 평균이다.
Davies-Bouldin Index
클러스터 간의 밀집도와 분리도를 측정하여 서로 잘 분리된 클러스터를 찾는 것을 목표로 한다.
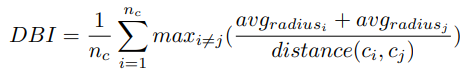
: 클러스터의 수
: 클러스터 와 클러스터의 centroid
: 클러스터 와 클러스터의 centroid
, : 각 포인트에서 각 클러스터의 centroid까지의 거리 평균
: 클러스터 와 의 centroid 사이의 거리
유클리드 거리를 기반으로 하며 클러스터가 구형이라고 가정하고, 클러스터가 불규칙한 모양을 가진다면 성능이 좋지 않을 수 있다. 또한 동일한 크기의 클러스터를 가정하므로 클러스터 크기가 불균형한 경우에는 적합하지 않다. 클러스터 개수를 알 수 없거나 클러스터링 알고리즘이 다른 수의 클러스터를 생성하는 경우, 제대로 작동하지 않을 수 있다. 하지만 위의 가정이 모두 만족된다면 좋은 결과를 얻을 수 있다.
Dunn's Index
클러스터의 밀집도와 분리도에 초점을 둔다. 클러스터 내의 포인트 간 최대 거리를 최소화하고 클러스터 중심 간의 거리는 최대화하는 것 사이의 균형을 찾는 것을 목표로 한다.
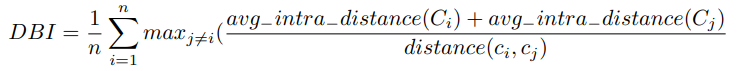
n: 클러스터의 수
: 클러스터
: 클러스터 에서의 평균 거리
: 클러스터 와 의 center 사이의 거리
이상치에 민감하고 거리 측정법에 크게 의존한다. 클러스터가 구형이라고 가정한다. 클러스터가 구형이 아닌 모양인 경우 클러스터 간의 실제 분리를 정확하게 반영하지 못한다. Dunn's Index는 숫자 결과를 생성하지만 '좋음', '나쁨'으로 해석하는 것은 주관적이다.
External Evaluation Metrics (when ground truth is available)
Adjusted Rand Index (ARI)
클러스터 분석과 ML에서 두 클러스터링 솔루션의 유사성을 평가하는데 널리 사용된다. 클러스터링 알고리즘에서 지정한 레이블과 실제 레이블 간의 일치를 측정한다.
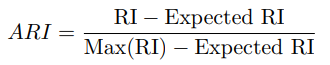
: 정답과 예측된 클러스터링 간의 일치 비율(동일한 클러스터에 있는 경우와 다른 클러스터에 있는 경우)
: 클러스터링이 랜덤하게 이루어질 때의 기대치
: 가 가질 수 있는 최대값으로, ARI 값을 [-1, 1] 범위로 정규화하는 역할
ARI는 불균형 클러스터 크기에 민감하다. 다른 클러스터의 샘플 수에 큰 차이가 있는 경우, ARI는 더 큰 클러스터에 편향될 수 있다.
ARI는 클러스터의 실제 수를 알고 있으며, 클러스터 할당이 무작위로 이루어진다고 가정한다. 실제 클래스 정답에 대한 지식이 필요하며 비지도 학습 시나리오에서는 사용할 수 없다. 이러한 경우 대체 평가 지표가 필요하다. 그럼에도 불구하고 ARI는 클러스터링 평가에 널리 사용되고 해석 가능한 지표로 남아 있다.
Normalized Mutual Information (NMI)
클러스터링 알고리즘이 할당한 레이블과 실제 클래스 레이블 간의 일치도를 측정하여 precision과 recall을 모두 고려한다.
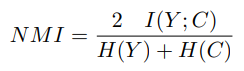
: 정답 레이블
: 클러스터링 알고리즘이 할당한 레이블
: 상호정보
: 각각 와 의 엔트로피
NMI의 범위는 0부터 1까지이다. 0은 상호 정보가 없음을 나타내고, 1은 정답 레이블과 예측 레이블 간에 완벽한 일치를 의미한다. NMI는 대부분의 클러스터링 솔루션에서 일반적으로 사용되는 지표이다. 한계점은 각 클러스터가 단일 클래스에 해당한다고 가정하는 것이다.
Discussion
현재 연구자들은 클러스터링 알고리즘을 효과적으로 적용하고 고유한 요구사항을 해결하는데 적용할 수 있는 방법을 탐구하고 있다. 딥러닝에서 클러스터링 알고리즘의 발전이 눈에 띄는 추세가 나타났다. 구체적으로, 신경망과 같은 딥러닝 기술을 클러스터링 알고리즘에 통합하여 성능을 개선하려는 추게사 분명해지고 있다. 특히 고차원 및 복잡한 데이터 처리에 적합하다. 또한, 하이브리드 클러스터링 방법의 인기가 점점 높아지고 있다. 이는 다양한 클러스터링 알고리즘을 결합하거나 클러스터링을 다른 머신러닝 기술과 통합하는 방법이다.
현재 클러스터링 알고리즘이 직면한 주요 과제는 최적의 클러스터 수를 결정하는 것이다.
모든 유형의 데이터와 응용 분야에서 다른 방법보다 보편적으로 우수한 단일 방법은 없다. 따라서 클러스터링 방법의 선택은 작업에 따라 크게 달라진다.