클러스터링

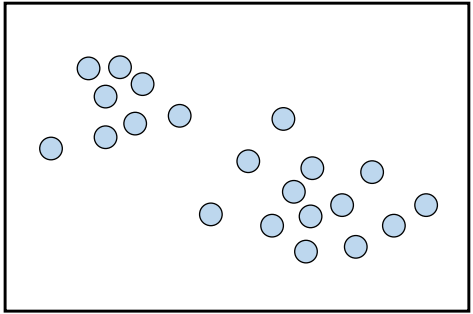
• 비지도 학습에서 데이터 샘플들을 별개의 군집(cluster)으로 그룹화하는 것

• 비지도 학습에서의 분류 알고리즘

• 데이터의 특징에 따라 세분화하는데 사용

• 이상 검출(anomaly detection)에 사용

• 유사성이 높은 데이터를 동일한 그룹으로 분류

• 서로 다른 군집은 특성이 상이하도록 군집화 함

• 클러스터 내부의 분산(within 분산) 최소화, 클러스터 간의 분산(between 분산) 최대화
  

• 모수적(parametric) 추정: 주어진 데이터가 특정 데이터 분포를 따른다고 가정
  ex) Gaussian Mixture Model(GMM)

• 비모수적(non-parametric) 추정: 데이터가 특정 분포를 따르지 않는다는 가정 하에서 확률 밀도를 추정
  ex) K-means, Mean Shift, DBSCAN

K-means

• 군집의 중심점(centroid) 기반 클러스터링
• 샘플은 가장 가까운 중심점을 가진 군집으로 할당됨
• 사전에 군집의 수에 대한 하이퍼파라미터 k를 정해야 사용 가능
• EM 알고리즘을 통해 최적의 군집에 수렴할 때까지 학습함

K-means의 한계점

• 군집의 개수, centroid에 대한 초기 설정값에 따라 성능 편차가 심함
• 군집 크기나 밀도가 다를 경우, 학습이 잘 안 될 수가 있음
• 데이터 분포가 특이할 경우에도 군집 학습이 어려움
  

EM 알고리즘

• 기댓값 최대화 알고리즘
• 최대가능도(maximum likelihood)나 최대사후확률(maximum a posteriori)을 갖는 모수의 추정값을 찾는 반복적인 알고리즘
• Expectation(기댓값) 단계: 현재의 추정된 모수를 통해 샘플을 군집에 할당하는 단계
• Maximization(최대화) 단계: 로그 가능도(likelihood)의 기댓값을 최대화하는 모수를 추정하는 단계
• 특정 분포에 대한 가정이 없는 non-parametric 추정에서는 가능도의 개념이 없음
• Mean Shift나 DBSCAN은 밀도 추정의 방법으로 학습
• K-means 군집화에서의 EM 알고리즘
  - Expectation 단계: 추정하고자 하는 모수는 중심점(centroid)이므로, 샘플을 군집으로 할당하는 단계
  • Maximization 단계: 가능도를 샘플이 군집에 속할 확률로 해석하여, 군집에 할당된 샘플을 바탕으로 새로운 중심점을 계산

EM algorithm in K-means

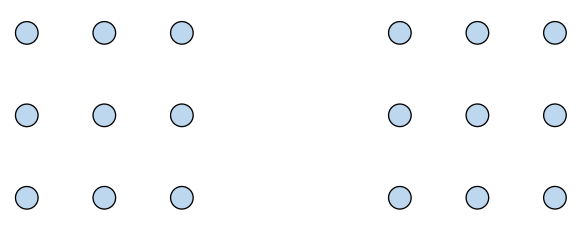
• 군집 수 k=2 인 상황
  

• 처음 군집의 centroid는 랜덤하게 설정함
  

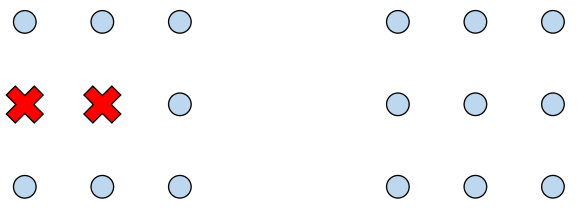
• 샘플들을 가장 가까운 centroid에 할당해 군집을 생성 -> E 단계
  

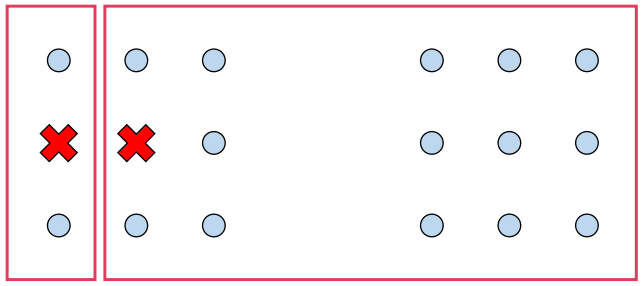
• 군집의 새로운 centroid를 계산 -> M 단계
  

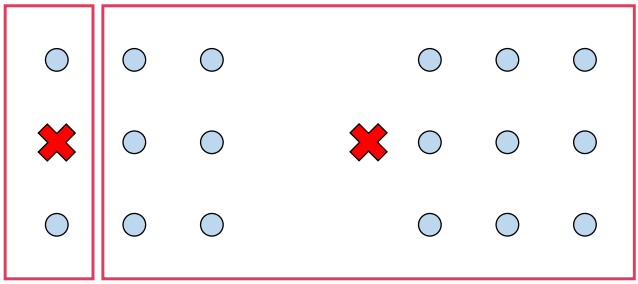
• 샘플들을 가장 가까운 centroid에 할당해 군집을 생성 -> E 단계
  

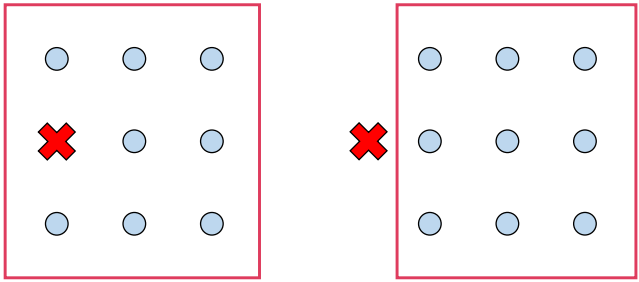
• 군집의 새로운 centroid를 계산 -> M 단계
  

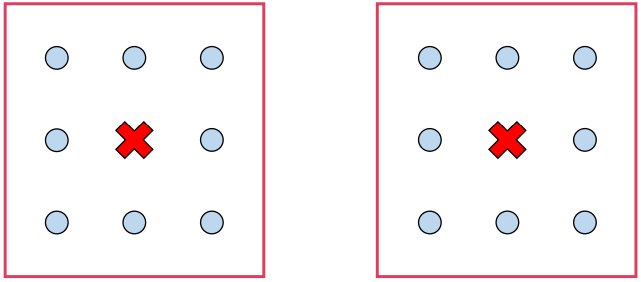
Evaluation Metrics of Clustering

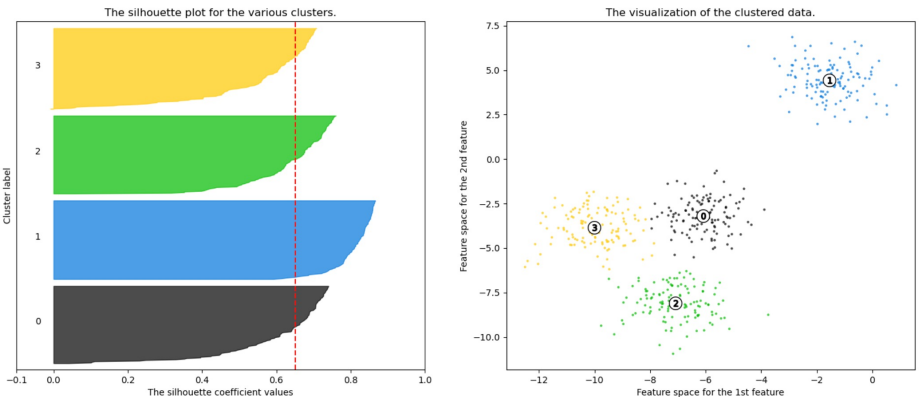
실루엣 분석(silhouette analysis)

• 군집들이 얼마나 효율적으로 분리되어 있는지를 보여줌

• 각 샘플들이 가지고 있는 실루엣 계수(silhouette coefficient)를 기반으로 함

• 전체 실루엣 계수의 평균값이 클수록, 개별 군집의 평균값의 편차가 작을수록 좋음

• 가장 가까운 타 군집 하나와의 거리를 통해 계산

• 실루엣 계수는 -1 ~ 1 사이의 값을 가짐, 1에 가까울수록 더 좋은 군집을 의미
  

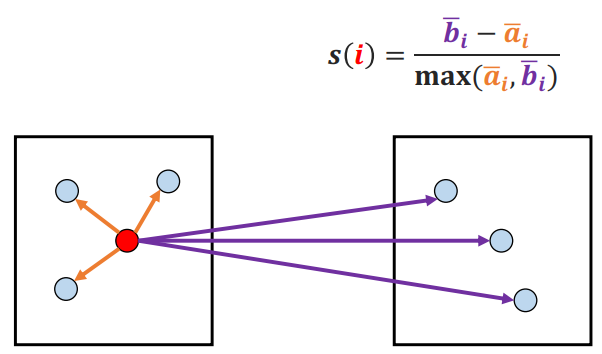
• 실루엣 계수의 평균값이 크고 편차가 작도록, K-means 알고리즘의 군집 개수(k)를 결정함
  

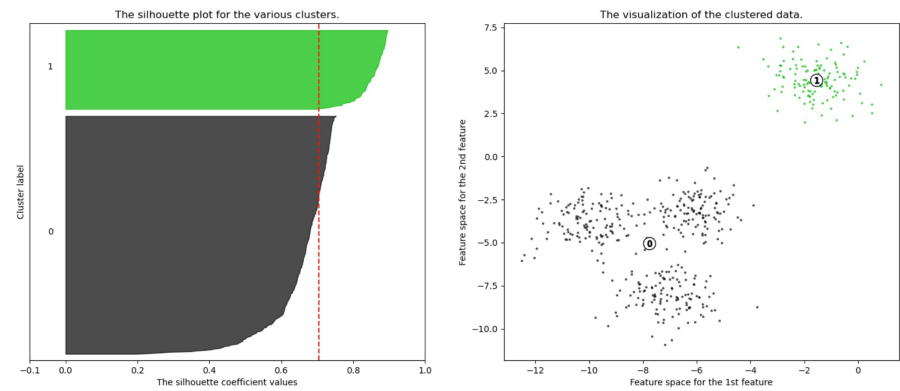
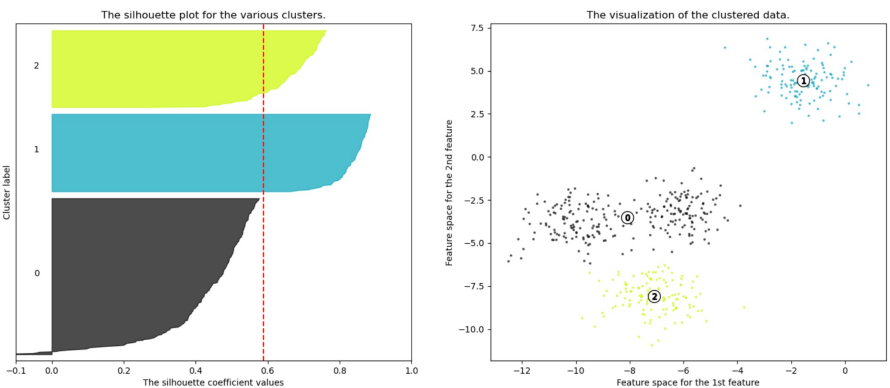
Mean Shift

• 평균 이동(mean shift)

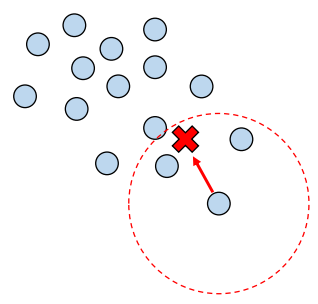
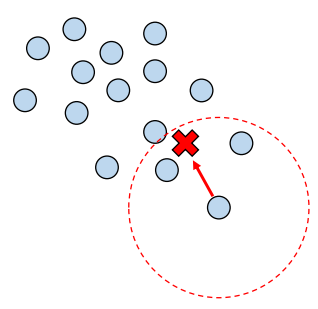
• 각 샘플을 기점으로 주변에 데이터가 가장 밀집된 곳으로 이동하는 것을 수렴할 때까지 반복

• 모든 데이터에 대해 수렴 지점을 계산하여 군집의 개수를 결정

• 각 샘플들을 가장 가까운 중심점을 가진 군집으로 할당
  

• 군집 개수에 대한 하이퍼파라미터가 불필요

• sliding window의 크기를 조절해 주변 어느 정도까지 볼지 결정해야 함
  

• 비모수(non-parametric) 방법의 모델

• KDE(kernel density estimation)를 통해 밀도가 가장 높은 곳을 찾아냄

KDE(kernel density estimation)

• 커널 함수를 통해 어떤 변수의 확률 밀도 함수를 추정하는 방법
• 개별 샘플들에 커널 함수를 적용한 값을 모두 합한 뒤, 데이터 개수로 나누어 확률 밀도 함수를 추정

Mean Shift 한계점

• sliding window의 크기와 bandwidth h에 대한 선택이 필요함
• 여전히 데이터 분포가 특이할 경우에 군집 학습이 어려움

DBSCAN

• density-based spatial clustering of applications with noise

• 밀도가 높은 부분을 중심으로 군집화를 하는 방법론

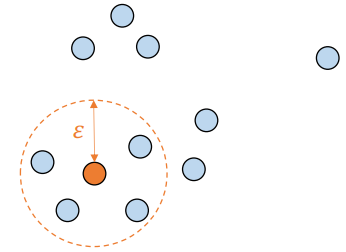
• 어떤 점을 기준으로 반경 ε 내에 샘플이 minpoints보다 많으면 같은 군집으로 할당
  

• 군집으로 할당된 샘플들을 해당 군집의 corepoint로 설정해 계속 반복

• minpoints 개수를 만족 못하는 borderpoint 샘플이 나올 경우 멈춤

• 모든 데이터 샘플에 대해 진행하여 cluster point와 noise point를 구분

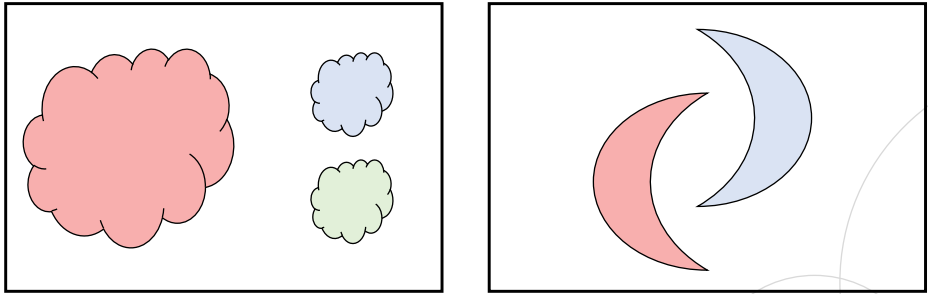
• (장점) 다양한 형태의 군집 유형을 구분할 수 있음

• (장점) 아웃라이어(noise point)를 찾아낼 수 있음

• (단점) 군집의 개수 설정에선 자유롭지만 ε과 minpoints에 대한 설정이 필요

• (단점) 연산량이 크기 때문에 시간이 오래 걸림

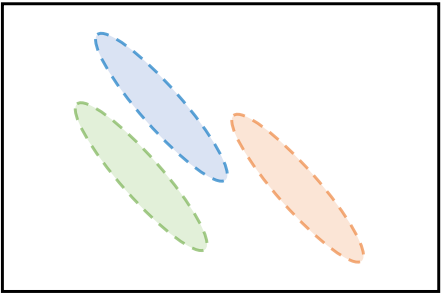
Gaussian Mixture Model(GMM)

• 모수적 추정의 방법론으로 주어진 데이터를 k개의 gaussian 분포의 혼합으로 가정

• EM 알고리즘을 통해 모델을 학습함
  

• E 단계: 현재의 추정된 모수를 통해 샘플을 군집에 할당하는 단계. responsibility(책임값)를 계산하여 샘플마다 가장 큰 값을 도출하는 군집으로 할당

• M 단계: 로그 가능도(likelihood)의 기댓값을 최대화하는 모수를 추정하는 단계

• (장점) 각 유형별 데이터의 밀도가 일정하지 않거나 경계가 모호해도 군집화가 잘됨

• (단점) 클러스터 개수 k에 대한 설정이 필요

• (단점) 데이터가 정규 분포의 조합으로 표현된다는 가정이 어긋나면 성능이 떨어짐

• (단점) 연산량이 크기 때문에 대량의 데이터에 사용하기 어려움

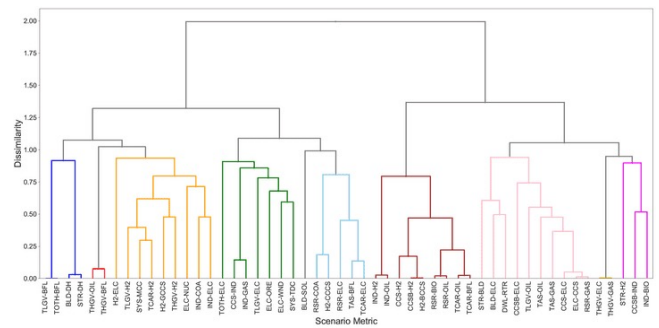
Hierarchical Clustering

• 계층적 군집화
• 하나의 클러스터로부터 시작해서 모든 클러스터가 하나의 원소를 가질 때까지 쪼개는 Divise(top-down approach) 방법
• 각각의 샘플을 원소로 가지는 클러스터들로부터 전체를 포함하는 하나의 클러스터가 될 때까지 합쳐가는 Agglomerative(bottom-up approach) 방법
• 군집-군집 간 거리 계산을 통해 합치거나 나눔

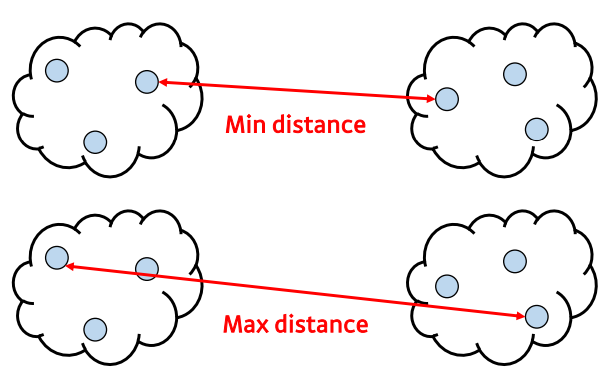
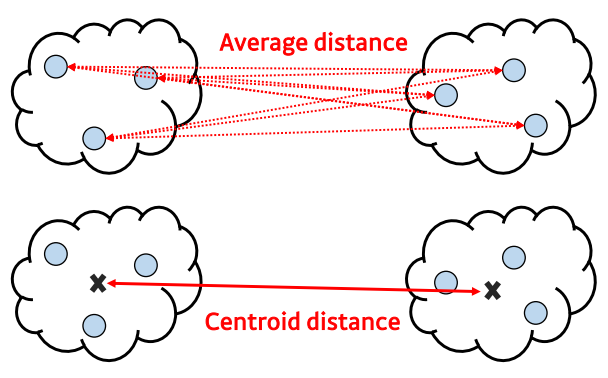
• 데이터 세분화에 보다 적합한 방법론
• 사전에 클러스터의 수를 정하지 않아도 학습이 가능함
• dendrogram으로 개체들이 결합되는 순서를 시각화함