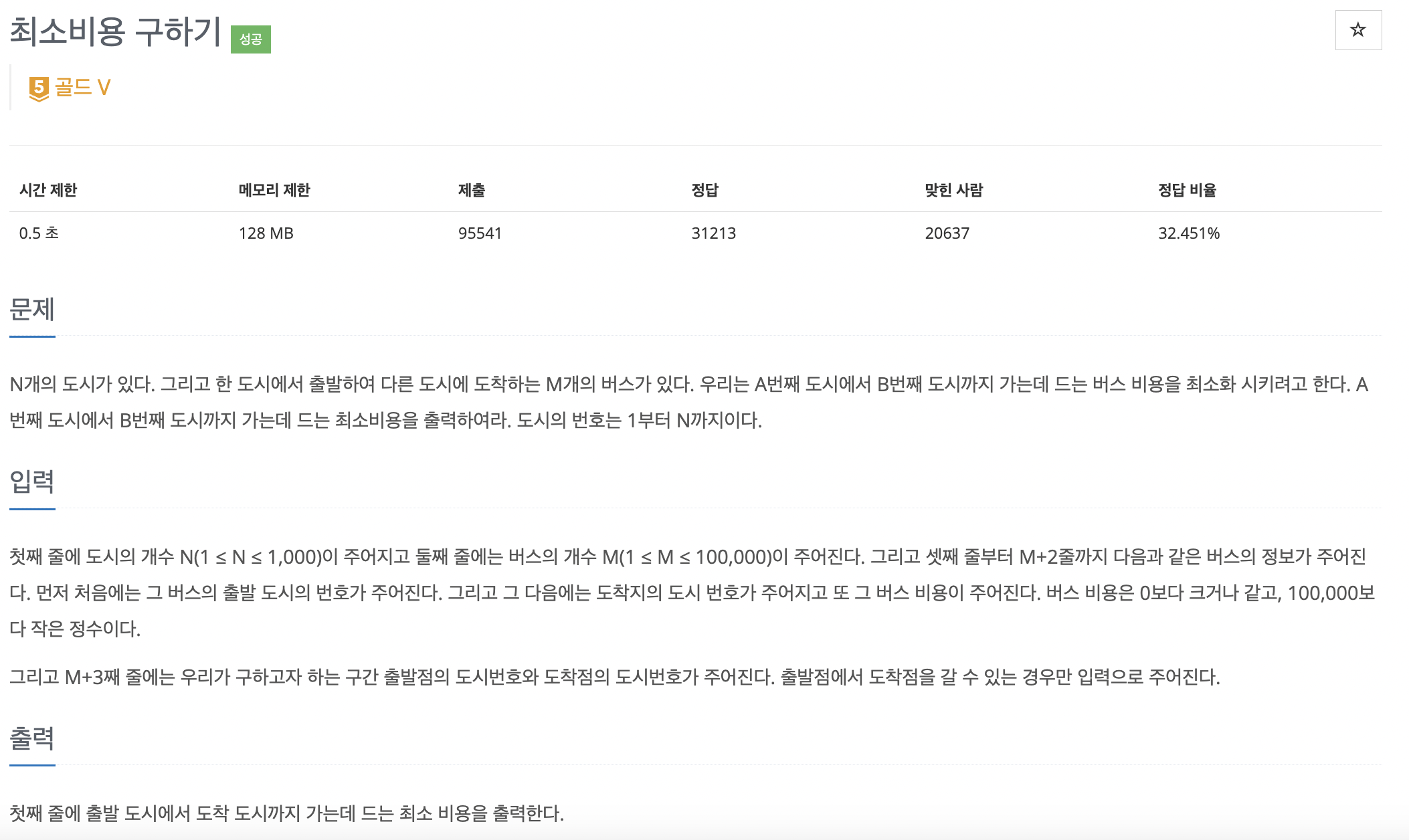
문제
풀이
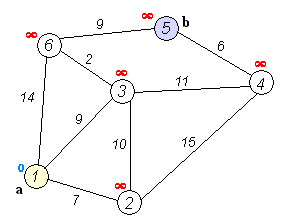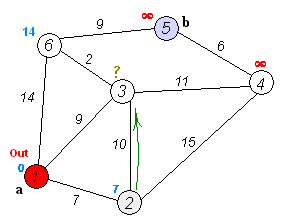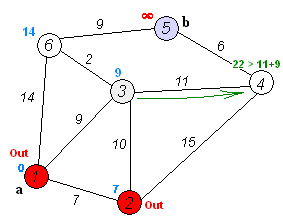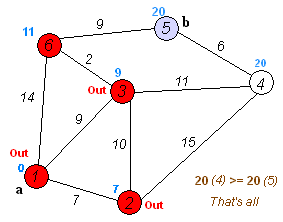
한 노드(출발 도시)에서 도착 노드(도착 도시)까지 가는 최단 경로를 구하고 싶을 때는 데이크스트라 알고리즘을 사용하면 된다.
데이크스트라(Dijkstra) 알고리즘
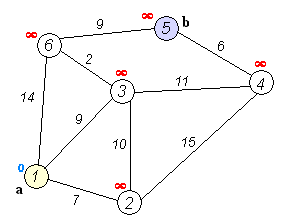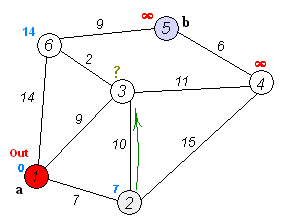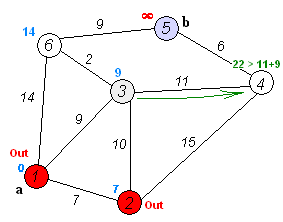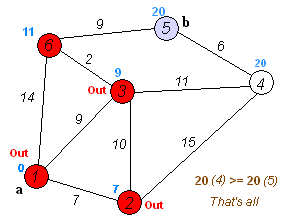
데이크스트라 알고리즘은 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘을 말한다.
데이크스트라(Dijkstra) vs 플로이드 워셜(Floyd Warshall)
Dijkstra 알고리즘은 하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이고,
Floyd Warshall 알고리즘은 모든 정점에서 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
예를 들어, GPS 시스템에서 특정 출발 위치에서 모든 목적지로의 최단 경로를 찾는 경우에는 Dijkstra 알고리즘을 사용하고, 도시 간의 최단 거리를 찾는 경우나 네트워크에서 모든 호스트 간의 최단 경로를 찾을 때는 Floyd Warshall 알고리즘을 사용할 수 있다.
알고리즘
-
출발점으로부터의 최단거리를 저장할 배열
d[v](v는 정점의 총 개수)를 만들고, 출발점에는 0을, 출발 점을 제외한 다른 노드들에는 INF를 넣는다. -
정점 A에서 갈 수 있는 임의의 노드 B에 대해
d[A] + P[A][B](A와 B사이의 최단 거리)와d[B]의 값을 비교한다. (INF와 비교할 경우 무조건 전자가 작다) -
만약 전자가 값이 작다면(더 짧은 경로라면),
d[B]의 값을d[A] + P[A][B]값으로 갱신시킨다. -
A의 모든 이웃 노드 B에 대해 이 작업을 수행한다.
-
A는 모든 노드를 방문했으니
방문 완료처리하고 더이상 A를 사용하지 않는다. -
미방문상태인 노드들 중, 출발점으로부터의 거리가 제일 짧은 노드 하나를 골라서 그 노드를 A에 저장한다.
-
도착 노드가
방문 완료상태가 되거나, 혹은 미방문 상태의 노드를 선택할 수 없을 때 까지, 2~7의 과정을 반복한다. -
이 작업을 마친 뒤, 도착 노드에 저장된 값이 바로 A로부터의 최단 거리이다.
순차 탐색 구현
6번 단계(미방문 노드 중 거리 값이 가장 작은 노드 찾기)에서 순차 탐색을 하는 경우 노드의 개수 만큼 순차 탐색을 수행해야 하기 때문에 O(N²)의 시간이 걸린다.
입력 받는 부분
// 입력 받기
let fs = require("fs");
let [N, M, ...input] = fs
.readFileSync("./Baekjoon/input.txt")
.toString()
.trim()
.split("\n");
N = +N; // 도시의 개수
M = +M; // 버스의 개수
// 출발 도시 start, 도착 도시 end
let [start, end] = input.pop().split(" ").map(Number);
// 버스의 정보
input = input.map((v) => v.split(" ").map(Number));
// 버스의 정보를 저장할 배열
let graph = Array.from({ length: N + 1 }, () => []);
// 출발도시 a의 도착 도시 b, 비용 c를 객체 형태로 저장
for (let [a, b, c] of input) {
graph[a].push({ node: b, cost: c });
}
// 최단거리를 저장할 배열
let dist = Array.from({ length: N + 1 }).fill(Infinity);
// 방문여부를 저장할 배열
let visited = Array.from({ length: N + 1 }).fill(false);구현 부분
/* 아직 방문하지 않은 노드 중
가장 거리값이 작은 노드 반환 */
function findSmallestNode() {
let min_dist = Infinity;
let min_node = 0;
for (let i = 1; i <= N; i++) {
if (!visited[i] && dist[i] < min_dist) {
min_dist = dist[i];
min_node = i;
}
}
return min_node;
}
// 데이크스트라
function dijkstra() {
dist[start] = 0;
visited[start] = true;
// 출발 도시에서 인접 도시까지의 최단거리 계산
graph[start].forEach((next) => {
dist[next.node] = Math.min(dist[next.node], next.cost);
});
for (let i = 1; i <= N; i++) {
let now_node = findSmallestNode();
visited[now_node] = true;
graph[now_node].forEach((next) => {
const acc = dist[now_node] + next.cost;
if (acc < dist[next.node] && !visited[next.node]) {
dist[next.node] = acc;
}
});
}
}
dijkstra();처음에 헤맸던 점
- 버스 정보를 받는 부분에서 편도인데 왕복이 가능하다고 생각했다. A -> B인 경우 B -> A도 성립한다고 생각함
for (let [a, b, c] of input) { graph[a].push({ node: b, cost: c }); //graph[b].push({ node: a, cost: c }); 이 부분이 필요 없다! } - 한 도시에서 다른 도시로 가는 버스편이 여러개 존재할 수 있음을 간과했다.
graph[start].forEach((next) => { // 여러 버스편 중 가장 비용이 적은 버스편을 채택 dist[next.node] = Math.min(dist[next.node], next.cost); });
데익스트라 알고리즘은 순차 탐색을 사용하는 경우 탐색 시간이 오래걸리기 때문에 보통 우선순위 큐를 사용한다고 한다. 지금은 순차 탐색으로 통과했지만 순차 탐색으로 안되는 경우 javascript로 우선순위 큐를 구현하는 방법을 알아봐야겠다. 🥹
출처: https://ko.wikipedia.org/wiki/%EB%8D%B0%EC%9D%B4%ED%81%AC%EC%8A%A4%ED%8A%B8%EB%9D%BC_%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://namu.wiki/w/%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BC%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98