Graph

그래프란?

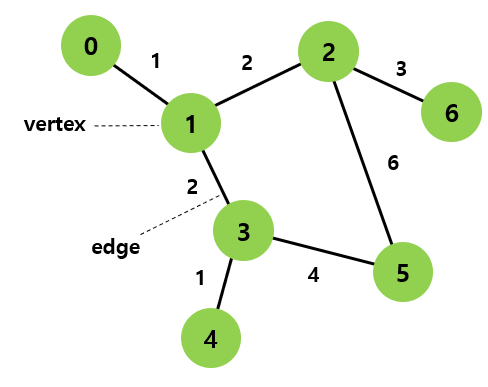
여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
각 원은 vertex(정점) , 각 선은 edge(간선)라고 표현한다.

• undirected graph

  무방향 그래프 : 방향성이 없어서 vertex1에서 vertex2로, vertex2에서 vertex1로 왕래가 가능하다. (ex. 인스타그램 like, 팔로우)

• directed graph

  단방향 그래프 : 방향성이 있어서 vertex1에서 vertex2로 가는것이 가능하다면, vertex2에서 vertex1로는 갈 수 없다. (ex. 카톡메시지)

• in-degree / out-degree

  진입차수 / 진출차수 : 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타냄

• adjacency

  인접 : 두 vertex간에 edge가 연결되어 있다면 두 vertex는 서로 adjacency하다.

• self loop

  vertex에서 출발한 간선이 곧바로 자기자신에게 돌아올때 자기 루프를 가졌다고 표현한다.( 다른 정점은 거치지 않는 것이 특징이다.)

• cycle

  한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다.

그래프의 표현 방식: 인접 행렬 & 인접 리스트

• 인접 행렬

  서로 다른 정점들이 인접한 상태인지를 표현한 2차원 배열의 형태. 이어져 있다면1 , 이어져 있지 않다면 0으로 표시한다. 만약 가중치 그래프라면 1대신 다른 의미 있는 값을 저장한다.

  /*
  				ToVertex
  		 	  	 0  1  2
  		  	0	[0, 0, 0],
  	FromVertex 	1	[0, 0, 0],
  		  	2	[0, 0, 0]
  */

• 인접 리스트

  
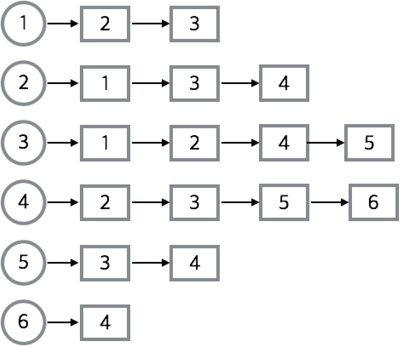
  메모리를 효율적으로 사용하고 싶을 때 인접 리스트를 사용한다.
  (인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지한다.)

Tree

트리구조란 ?

나무를 거꾸로 매달았을때의 모습과 비슷한 구조를 의미하며, 데이터가 바로 아래에 있는 하나 이상의 데이터에 무방향으로 연결된 계층적 자료구조다

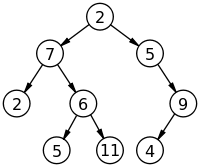
Root라는 (이미지에선 제일 위에 있는 2) 하나의 꼭짓점을 시작으로 여러개의 데이터를 edge로 연결한다.
각 데이터를 node라고 하며, 두개의 노드가 상하계층적으로 연결되면 부모/자식노드라고한다.
(9는 4의 부모노드, 4는 9의 자식노드)
자식이 없는 노드는 나뭇잎 같다고 해서 leaf node라고 불린다.

• depth

  깊이 : 루트 노드는 지면에 있어서 깊이 0이고 [7,5]의 깊이는 1 [2,6,9]의 깊이는 2 [5,11,4]의 깊이는 3이다.

• 레벨

  같은 깊이를 가지고 있는 노드를 묶어서 레벨로 표현할 수 있다. depth가 0인 루트의 레벨은 1이고 [7,5]의 레벨은 2 [2,6,9]의 레벨은 3 [5,11,4]의 레벨은 4이다. 같은 레벨에 있는 노드를 Sibling Node(형제노드)라고 한다.

• 높이

  깊이의 반대이다. [5,11,4,2]는 높이 0 , [6,9]는 높이 1 , [7,5]는 높이 2 , [2]는 높이 3을 갖는다.

• 서브트리

  [7,2,6] , [6,5,11] 와 같이 큰 트리 내부의 작은 트리를 서브 트리라고 부른다.

Tree traversal ?

특정 목적을 위해 모든 노드를 한번씩 방문하는 것을 트리 순회 라고 한다.
주로 3가지 방법을 사용한다

• 전위 순회

  

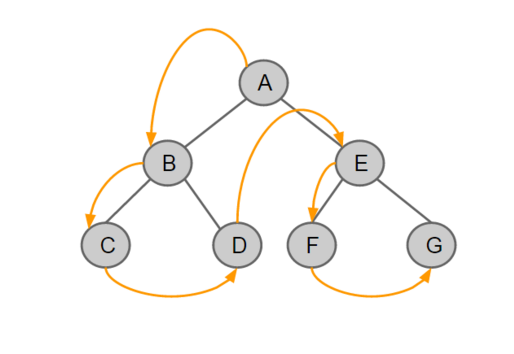
• 중위 순회

  

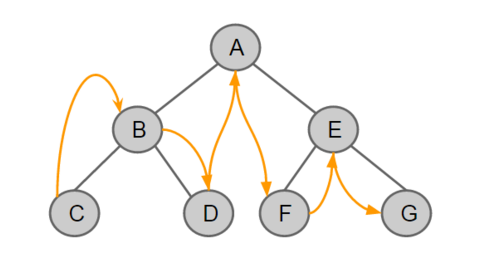
• 후위 순회

  

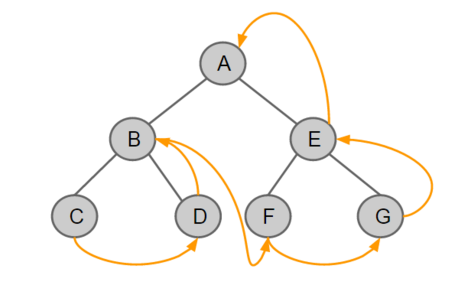
BST

이진트리란?

자식 노드가 최대 두 개인 노드들로 구성된 트리이다.
이 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있다.
이진트리는 자료의 탐색/삭제 방법에 따라 아래 3가지로 나뉜다.

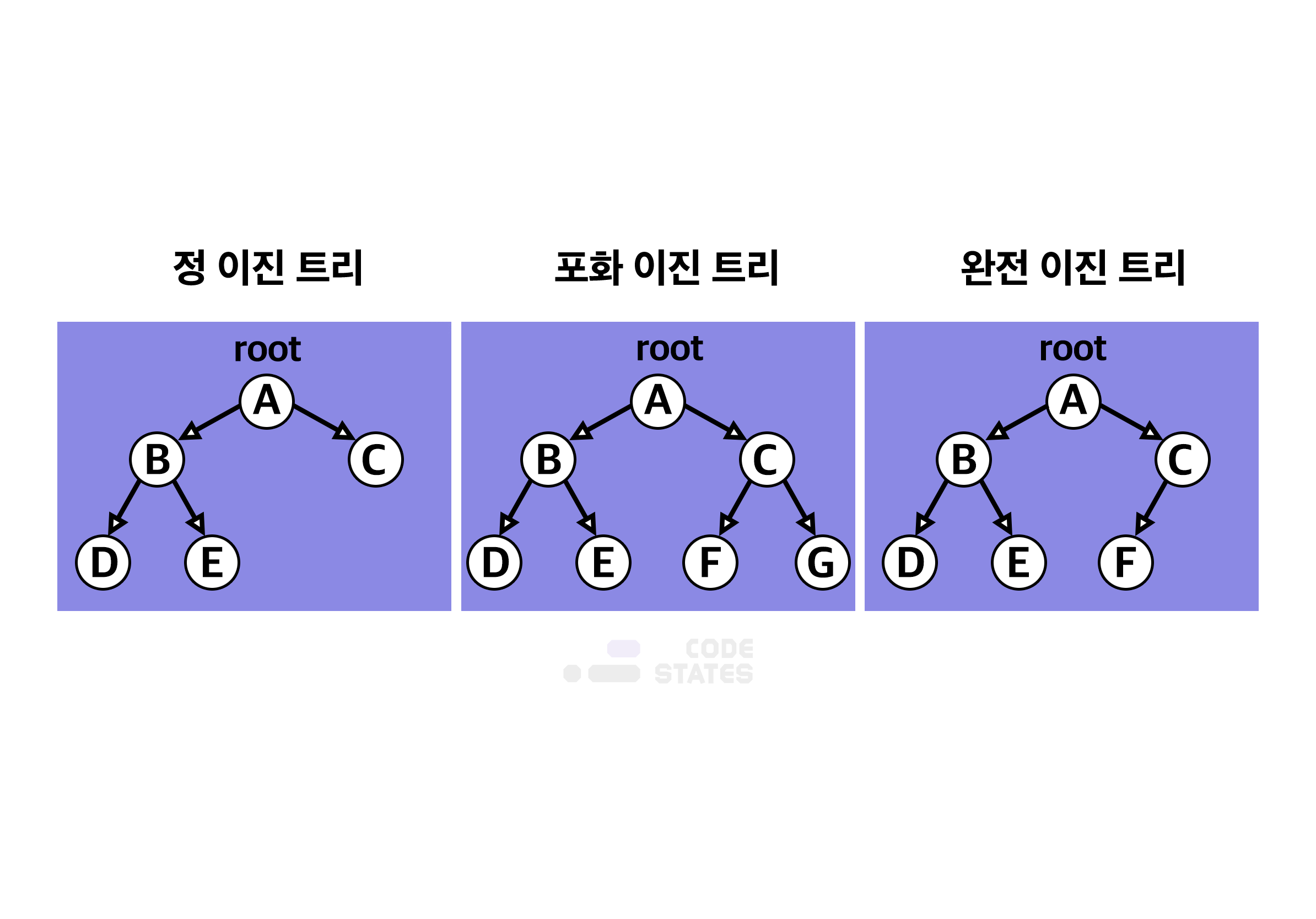
이진 트리 종류	영어 표기	설명
정 이진 트리	Full binary tree	각 노드가 0 개 혹은 2 개의 자식 노드를 갖습니다.
포화 이진 트리	Perfect binary tree	정 이진 트리이면서 완전 이진 트리인 경우입니다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리입니다.
완전 이진 트리	Complete binary tree	마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 합니다.

BFS

Breadth-First-Search

너 비 우 선 탐 색

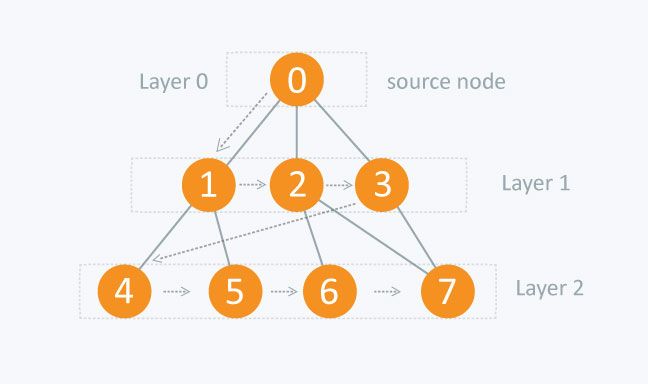
function bfs(root) {
  let queue = [root];
  let ret = [];
  while(queue.length) {
    let node = queue.shift();
    ret.push(node.val);
    if(node.left) queue.push(node.left);
    if(node.right) queue.push(node.right);
  }
  return ret;
}

DFS

Depth-First-Search

깊 이 우 선 탐 색

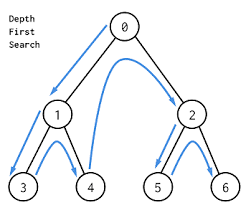
( 미로에서 왼손에 벽을 짚고 출구까지 가던것을 생각하면 된다. )

// with recursion
function dfs(root) {
  if(root === null) return [];
  return [...dfs(root.left), root.val, ...dfs(root.right)];
}
// with stack
function dfs(root) {
  let stack  = [];
  let ret = [];
  let node = root;
  while(node || stack.length) {
    while(node !== null) {
      stack.push(node);
      node = node.left;
    }
    node = stack.pop();
    ret.push(node.val);
    node = node.right;
  }
  return ret;
}

BFS는 QUEUE ! DFS는 STACK(or recursion) !

자료구조에서 BFS나 DFS를 만나면 queue와 stack/recursion부터 떠올리자.

알고리즘풀이

95~97 총 3문제를 풀었다.