지난 포스팅에서 순열과 조합 알고리즘을 이미 구현한 바 있다.(링크)
오늘 코플릿 시간에 중복순열에 관련된 문제까지 풀게 되어 이 내용까지 합하여 다시 포스팅하고자 한다. 왜냐면 세 알고리즘에서 규칙을 찾았기 때문(rest 배열)!!!
순열, 조합, 중복순열 구하기
기본 규칙
순열, 조합, 중복순열 모두 같은 로직으로 진행된다.
배열에서 3개를 선택하는 경우
1. 하나의 수를 선택한다.
2. 3개를 뽑는 순열 중 하나의 수를 선택했으니 남은 배열에서 2개를 선택해야한다.
3. 남는 배열에서 1개를 선택할 때까지(재귀 탈출 조건) 2번 과정을 재귀적으로 반복한다.
이 세 과정을 반복하면 순열,조합,중복순열을 구할 수 있다.
순열, 조합, 중복순열들은 서로 남은 배열을 설정해주는 과정에서만 차이가 있다. (이번에 새로 알게 된 사실!!!)
순열
수도코드는 아래와 같았다.
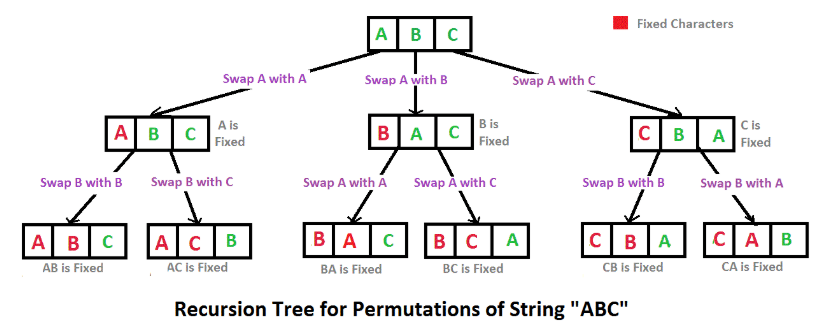
1(fixed) => permutation([2, 3, 4]) => 2(fixed) => permutation([3, 4]) => ...
2(fixed) => permutation([1, 3, 4]) => 1(fixed) => permutation([3, 4]) => ...
3(fixed) => permutation([1, 2, 4]) ... 위와 동일...
4(fixed) => permutation([1, 2, 3])이를 코드로 나타내어 보면 아래와 같다.
const getPermutations = function (arr, selectNumber) {
const results = [];
//아래 if는 재귀 탈출 조건
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = [...origin.slice(0, index), ...origin.slice(index+1)]
// 해당하는 fixed만을 제외한 나머지 배열(양옆으로 쪼깨고 다시 붙인다)
const permutations = getPermutations(rest, selectNumber - 1);
const attached = permutations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}이 규칙만 이해한다면 조합과 중복 순열은 손쉽게 생각할 수 있을 것이다.
조합
- 조합은 선택했던 모든 것들은 다시는 선택하면 안 되기 때문에 rest 배열이 fixed의 이후의 범위로 좁혀지면 된다.
const getCombinations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = origin.slice(index + 1);
// 해당하는 fixed를 제외한 나머지 뒤
const combinations = getCombinations(rest, selectNumber - 1);
const attached = combinations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}중복 순열
- 중복 순열은 현재 fixed까지 다시 선택할 수 있기 때문에 rest 배열이 매번 기본 arr이면 된다. (기본 arr은 forEach구문의 3번째 인자를 활용하면 된다.)
const getPermutations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = origin
// 일반 순열알고리즘에서 위의 rest 만 origin로 바뀐다
const permutations = getPermutations(rest, selectNumber - 1);
const attached = permutations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}예시문제
문제
평범한 블랙잭 게임에서 수시로 패배하자 흥미가 떨어진 김코딩은 박타짜에게 게임룰을 변형하여 새로운 카드 놀이를 해 볼 것을 제안합니다.
새로운 룰은 다음과 같습니다.
1. 숫자로 이루어진 카드를 여러 장 받습니다.
2. 3장씩 카드를 고르고, 3장에 적힌 숫자들의 합이 소수인지 확인합니다.
3. 받아든 카드로 만들 수 있는 소수의 개수가 많은 사람이 이기게 됩니다.
예로, [1, 2, 3, 4]라는 카드를 받았을 때 만들 수 있는 숫자는 6, 7, 8, 9이고, 소수는 7 하나이기 때문에 가지고 있는 소수의 개수는 1개입니다.
[2, 3, 4, 8, 13]라는 카드를 받았을 때 만들 수 있는 숫자는 9, 13, 18, 14, 19, 23, 15, 20, 24, 25이고, 소수는 13, 19, 23 총 3개이기 때문에 가지고 있는 소수의 개수는 3개입니다.게임을 진행하기 전에 소수에 대해 아무런 지식이 없는 박타짜는 게임을 며칠 미룬 뒤, 게임의 룰을 따르는 함수를 만들기로 했습니다.
소수에 약한 박타짜를 도와 여러 장의 카드 중 세 장씩 조합해 소수가 되는 경우의 수를 리턴하는 함수를 완성해 주세요.
수도코드
// cards 배열에서 먼저 3개를 선택하는 경우의 수를 모두 나열한 배열을 구한다(어차피 합이 중요하기 때문에 순서는 고려하지 않는 조합 함수 활용)
// 반복문을 사용하여 배열을 훑으면서
그 배열의 요소 합으로 배열의 요소를 변경한다.
변경할 때마다 그 수가 소수인지 아닌지 판별한다(소수판별함수 활용)
//따라서 이 함수는 조합함수 & 소수판별함수를 미리 선언해놓으면 편하다!코드로 나타내보면
function boringBlackjack(cards) {
// TODO: 여기에 코드를 작성합니다.
const getCombinations = function (arr, selectNumber) {
const results = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = origin.slice(index + 1);
const combinations = getCombinations(rest, selectNumber - 1);
const attached = combinations.map((el) => [fixed, ...el]);
results.push(...attached);
});
return results;
}
//1. 조합의 배열을 먼저 구하고
const resultArr = getCombinations(cards, 3)
//2. 그 배열의 요소 합으로 모두 변경하고 소수인지 아닌지 판별
let count = 0;
for(let i=0; i<resultArr.length; i++){
resultArr[i] = resultArr[i].reduce((acc, cur)=>acc+cur, 0)
if(isPrime(resultArr[i])){
count++
}
}
return count;
//소수인지 아닌지 판별하는 함수
function isPrime(num) {
let result = false;
if(num === 2)
return true;
for(let i = 2; i<=Math.floor(Math.sqrt(num)); i++){
if(num % i === 0){
result = false;
break;
}else result = true;
}
return result;
}
}