JavaScript로 부분집합(powerset) 알고리즘 구현하기

부분집합이란?

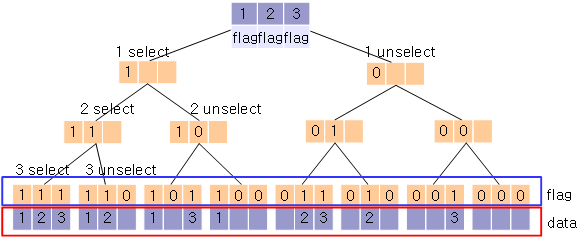
[1, 2, 3] 이란 배열이 주어진 집합이라고 할 때,
[1, 2, 3] 의 모든 부분집합은 아래 8개와 같다.

[] (공집합)
[1] [2] [3]
[1, 2] [1, 3] [2, 3]
[1, 2, 3]

따라서 멱집합은 위의 모든 부분집합들의 집합이므로
[ [], [1], [2], [3],  [1, 2], [1, 3], [2, 3], [1, 2, 3] ]
처럼 2차원 배열로 표현될 수 있다.

수도코드

[1, 2, 3] 
0. 우선 공집합 추가하고 []
1. 하나씩 뽑고 [1] [2] [3]
2. 두개씩 뽑고 [1, 2] [1, 3] [2, 3]
3. 세개 뽑자 [1, 2, 3]

각 집합 내 '요소의 개수'를 기준으로 뽑는 게 통상 우리가 부분집합을 만들 때 겪는 과정이다.
점점 0층(공집합)부터 3층(배열의 요소가 3개인 것)까지 층을 늘려나가면서 부분집합을 구하는 것을 볼 수 있다. 즉, 층에 따라서 어떤 숫자를 뽑을지 우리의 뇌는 계산한다. 층은 Depth First Search와 관련이 있다.

아래와 같이 부분집합을 나타내어 볼 수 있다.

[O, O, O] => [1, 2, 3]
[O, O, X] => [1, 2]
[O, X, O] => [1, 3]
[O, X, X] => [1]
[X, O, O] => [2, 3]
[X, O, X] => [2]
[X, X, O] => [3]
[X, X, X] => []

그리고 0층부터 3층까지 파고들 때 DFS 알고리즘을 적용할 수 있다.
(아래 사진: 검정색은 포함(true), 분홍색은 미포함(false)을 나타냄)

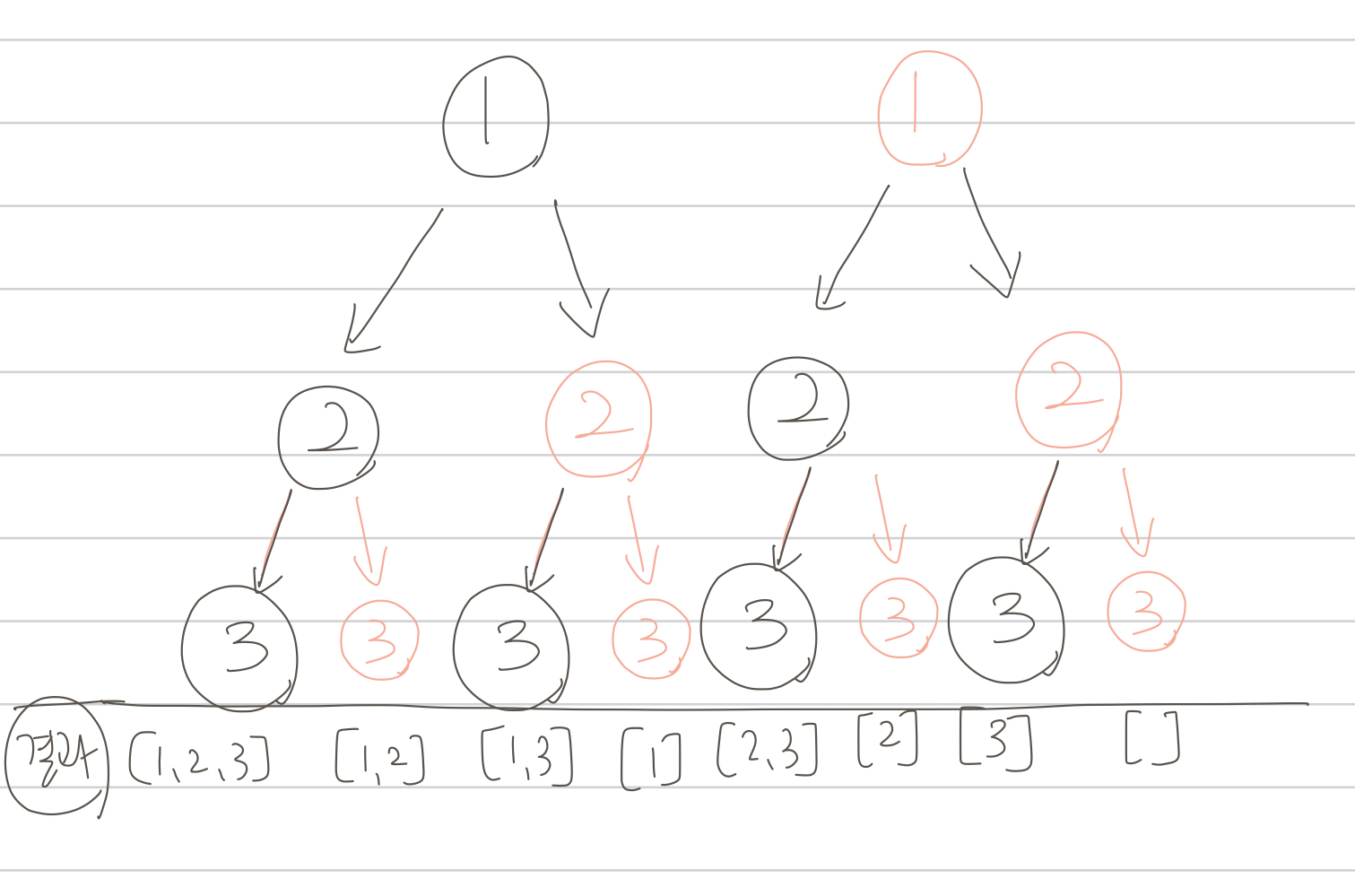
재귀의 탈출 조건은 층이 3층일때(배열의 길이와 같을 때)이다. 탐색하는 방법은 이진트리의 왼쪽과 오른쪽을 탐색하듯이 왼쪽으로 갈때에는 select=true=o를, 오른쪽으로 갈때에는 unselect=false=x를 해주면 된다.

코드로 나타내보면

const getSubsets = function (arr) {
  let flag = new Array(arr.length).fill(false);
  const subSets = [];

  const subSet = function DFS (depth) { // 부분 집합 구하는 재귀 함수, DFS 알고리즘
    if (depth === arr.length) { // 트리의 끝에 다다른 것 ==> 재귀 탈출 조건
      const subSet = arr.filter((el, index) => flag[index]); // arr의 인덱스에 맞춰서 그 인덱스 값이 flag에서 true인지? => true인것들로만 필터
      subSets.push(subSet); // 부분집합(한번 실행할 때 배열 1개)을 담는 배열에 push
      return ;
    }

    flag[depth] = true; // 해당 depth의 flag true = 트리의 왼쪽
    subSet(depth + 1); // 트리의 왼쪽에 대해 재귀호출

    flag[depth] = false; // 해당 depth의 flag false = 트리의 오른쪽
    subSet(depth + 1); // 트리의 오른쪽에 대해 재귀 호출
  }
  
  subSet(0); // depth 0 부터 시작
  return subSets;
}

재귀가 호출될 때마다(sebSet(depth+1)) 두개로 자식 노드들이 생기는 것과 같은 이진트리 형식과 비슷하다.

[1, 2, 3] 예시의 경우, 최종적으로 재귀탈출 조건을 만족하는 총 flag의 개수는 8개이고, 각각 배열 subSets에 push된다.