Big O Notation

알고리즘의 성능을 비교할때 사용하는 언어이다. 빅오 표기법은 dominant operations(우수한 성능?)에 관한 것이며 시간(얼마나 빠른지)과 공간(메모리가 얼마나 큰지)의 2개의 축을 사용한다.

func findNemo(_ arr: [String]) {
    let before = Date()
    
    for i in 0..<arr.count {
        if arr[i] == "nemo" {
            print("Found him!")
        }
    }
    
    let after = Date()
    let component = Calendar.current.dateComponents([.nanosecond], from: before, to: after)
    let milliSeconds: Double = Double(component.nanosecond! / 1000000)
    print("Finding nemo took: \(milliSeconds))")
}

let nemo = Array<String>(repeating: "", count: 100000)
findNemo(nemo)

배열 안에 니모를 찾는 함수가있다. 함수를 실행하면 니모를 찾았을때 "Found him!"을 출력하고 니모를 찾는데 얼만큼의 시간이 걸렸는지 출력해준다. count(배열 속 값의 개수)를 증가시킬 수록 시간도 증가하므로 count와 니모를 찾으려고 검색하는 수는 선형(linear)이다. 빅오 표기법에서는 이런 관계를 선형 시간(linear time) O(n)이라고 한다.

종류

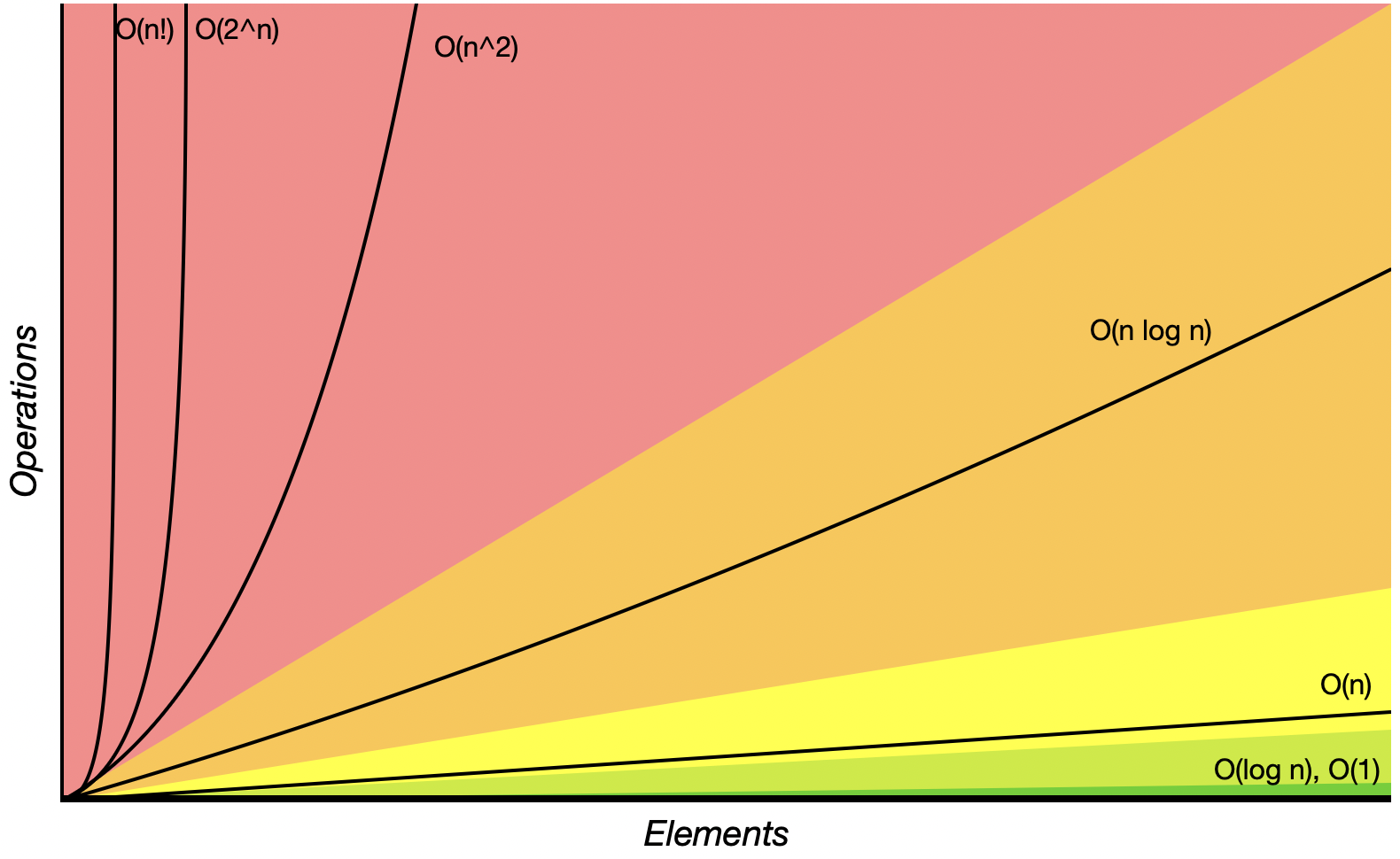
https://www.bigocheatsheet.com

알고리즘이 상수시간, 선형시간, 로그시간이면 좋다.

상수 시간 O(1)

// Constant time O(1)
func constantTime(_ n: Int) -> Int {
    let result = n * n
    return result
}

반복문이나 복잡한 로직 없이 그냥 계산만 하는 경우. 가장 빠르다.

선형 시간 O(n)

// Linear time O(n)
func linearTime(_ A: [Int]) -> Int {
    for i in 0..<A.count {
        if A[i] == 0 {
            return 0
        }
//        print(i)
    }
    return 1
}
linearTime([1, 2, 3])

반복문이 있고 인수로 전달받는 배열속 값이 얼마나 많은지에 따라 시간이 증가하는 경우.

로그 시간 O(log n)

// Logarithmic time O(log n)
func logarithmicTime(_ N: Int) -> Int {
    var n = N
    var result = 0
    while n > 1 {
        n /= 2
//        print(n)
        result += 1
    }
    return result
}
logarithmicTime(128)

값이 계속 반으로 줄어드는 경우. 이진트리같은 알고리즘에서 볼 수 있다.

2차 시간 O(n^2)

// Quadratic time O(n^2)
func quadratic(_ n: Int) -> Int {
    var result = 0
    for i in 0..<n {
        for j in i..<n {
            result += 1
//            print("\(i) \(j)")
        }
    }
    return result
}
quadratic(16)

반복문 안에 반복문이 있는 경우.

빅오 표기법은 최악의 경우를 생각했을 때가 기준이다.

Trading Off Space For Time

두 배열에서 같은 값이 있는지를 찾는 함수를 만들어야 한다고 했을 때 다음과 같이 만들 수 있다.

1번

// Naive brute force O(n^2)
func commonItemsBrute(_ A: [Int], _ B: [Int]) -> Bool {
    for i in 0..<A.count {
        for j in 0..<B.count {
            if A[i] == B[j] {
                return true
            }
        }
    }
    return false
}
commonItemsBrute([1, 2, 3], [4, 5, 6])
commonItemsBrute([1, 2, 3], [3, 5, 6])

위의 코드는 새로운 변수를 하나도 생성하지 않았지만 반복문 안에 반복문을 넣는 2차 시간 O(n^2)이므로 속도가 느리다.

2번

// Convert to hash and lookup via other index
func commonItemsHash(_ A: [Int], _ B: [Int]) -> Bool {
    
    // Still looping...but not nested - O(2n) vs O(n^2)
    var hashA = [Int: Bool]()
    for a in A { // O(n)
        hashA[a] = true
    }
    
    // Now lookup in the hash to see if elements of B exist
    for b in B {
        if hashA[b] == true {
            return true
        }
    }
    return false
}
commonItemsHash([1, 2, 3], [4, 5, 6])
commonItemsHash([1, 2, 3], [3, 5, 6])

위의 코드는 hashA라는 새로운 딕셔너리를 생성해서 반복문 2개 사용하는 방식으로 O(n)으로 속도를 높였다. 여기서 중요한 것은 새로운 딕셔너리를 만들었기 때문에 메모리를 더 사용해서 처리 시간을 단축시켰다는 점이다.

	시간	공간
1번	O(n^2)	O(1)
2번	O(n)	O(n)

Reducing

1. 최악의 경우만 표기한다.
   ex) O(1) + O(n) + O(n^2) = O(n^2)
2. 상수는 표기하지 않는다.
   ex) O(n) + O(n) + O(n) = O(3n) = O(n)
3. 더하기
   ex) O(n) + O(m) = O(n+m)
4. 곱하기
   ex) O(n) * O(m) = O(nm)