Graphs

그래프는 정점(vertex)과 간선(edge)로 이루어진 자료구조이다. 이진트리도 그래프의 한 종류인데 이진트리의 node가 정점이고 다음 노드를 나타내는 left, right가 간선이다. 그래프의 간선은 이진트리처럼 한 방향만 가거나 양방향으로도 이동할 수 있다. 또한 간선은 가중치(weight)를 가질 수 있다.

Graph Data Structures

Edge List

간선 리스트는 그래프의 모든 간선을 배열에 나열하는 간단한 방식이다. 모든 간선을 탐색해야 하므로 O(n)의 시간 복잡도를 가진다.

Adjacency Matrix

인접 행렬은 O(1)의 시간 복잡도를 가지고 있고 매우 빠르게 찾을 수 있다. 하지만 공간을 많이 차지한다.

Adjacency List

인접 리스트는 간선 리스트의 간단함과 인접 행렬의 빠른 장점을 모두 가지고 있다. 인접 리스트는 모든 정점의 간선들을 배열에 나열한다.

Example

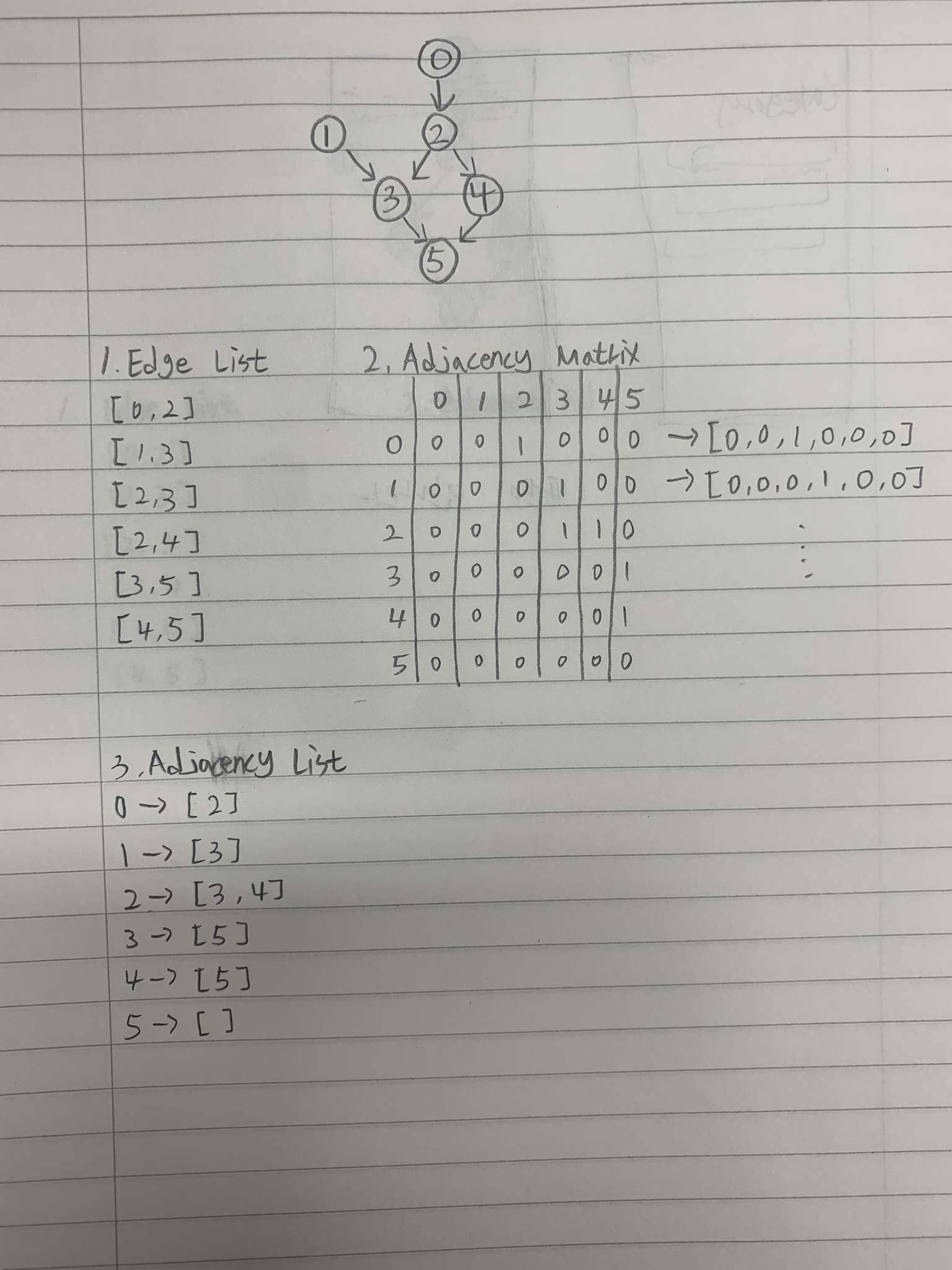
간선이 양방향일 경우 인접 행렬은 대각선을 기준으로 대칭을 이룬다.

Graph Algorithms

class Graph {
    var V = 0                       // number of vertices
    var adj = [[Int]]()             // adjacency list
    
    init(_ V: Int) {
        self.V = V
        for _ in 0..<V {
            adj.append([Int]())     // create empty array of adjacency lists
        }
    }
    
    func addEdge(v: Int, w: Int) {
        adj[v].append(w)
    }
    
    // BFS traversal from a given source s
    func BFS(s: Int) -> [Int] {
        
        var result = [Int]()
        
        // Mark all vertices as not visited
        var visited = adj.map { _ in false }
        
        // Create BFS Queue
        var queue = Queue<Int>()
        
        // Mark first vertex as visited and enqueue
        visited[s] = true
        print("Starting at \(s)")
        queue.add(s)
        result.append(s)
        
        while queue.count > 0 {
            let current = queue.remove()!
            print("De-queueing \(current)")
            
            // Get all the adjacent vertices of the current vertex
            // If adjacent has not being visited, mark visited and enqueue
            
            for n in adj[current] {
                if visited[n] == false {
                    visited[n] = true
                    print("Queuing \(n)")
                    queue.add(n)
                    result.append(n)
                }
            }
         }
        
        return result
    }
    
    // DFS traversal from a given source s
    func DFS(s: Int) -> [Int] {
        
        var result = [Int]()
        
        // Mark all vertices as not visited
        var visited = adj.map { _ in false }
        
        // Create DFS Stack
        var stack = Stack<Int>()
        
        // Mark first vertex as visited and enqueue
//        print("Starting at \(s)")
        visited[s] = true
        stack.push(s)
        
        while stack.count > 0 {
            let current = stack.pop()!
//            print("Popping \(current)")
            result.append(current)
            
            // Iterate over all neighbours adding to queue and popping deep as we go
            for n in adj[current] {
                if visited[n] == false {
                    visited[n] = true
//                    print("Pushing - \(n)")
                    stack.push(n)
                }
            }
        }
        
        return result
    }
}

Breadth First Search

너비 우선 탐색(BFS)은 중앙에서 시작해서 바깥쪽으로 넓혀가며 탐색하는 알고리즘이다. 가까운 이웃을 찾는다고 생각하면 되는데 곡 추천을 하거나 SNS에서 친구를 찾거나 게임에서 가까운 친구를 찾거나 할 때 사용된다. 큐(Queue)를 기반으로 사용한다.

Deapth First Search

깊이 우선 탐색(DFS)은 한 노드의 주변이 아닌 자식노드부터 탐색하는 알고리즘이다. 길을 찾거나 그래프에서 순환여부를 탐색할때 사용된다. 스택(Stack)을 기반으로 사용한다.