
1. operator (연산자)
예를 들어 다음과 같은 표현식이 있다고 가정해보자
1 + 2 * 3수학적으로는 x가 +보다 우선순위가 높아 2 * 3이 연산되고 1이 더해진다
그렇다면 컴파일러는 이를 어떤 방식으로 알 수 있을까?
연산자 우선순위
이러한 연산자들끼리의 우선순위는 미리 정해져있다, 우선순위가 높은 연산자와 피연산자는 컴파일 타임에 그룹화 된다
위의 연산자 우선순위를 전부 외우기는 힘드니 우선 연산이 필요하다면 ( )로 명시적으로 먼저 연산될 연산자와 피연산자를 그룹화 시킬 수 있다
(a * b) + (c * d)이와 같은 경우 (ab)가 (cd)보다 먼저 계산된다는 보장이 없다 (뭐가 먼저 연산되든 중요하지 않음)
산술 연산자
단항 산술 연산자는 단항이기 때문에 피연산자를 하나만 가지는 연산자이다
+와 -가 있고 각각은 값에 +1, -1을 곱한 값을 반환한다
(+5, -4)
단항 산술 연산자는 피연산자와 공백 없이 사용한다 (- 5 (x))
이진 산술 연산자는 피연산자를 2개를 가지는 연산자이다
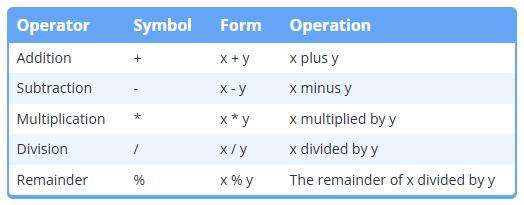
나눗셈 시 주의할 점
이때 나눗셈의 경우 피연산자 중 하나라도 실수라면 실수 나누기를 실행한다 (둘다 정수면 정수 나누기)
(결과값이 실수, 정수로 나온다는 의미)
만약 정수 타입 변수끼리를 이용하여 실수 나누기를 하고 싶다면 캐스팅을 해야한다
constexpr int a{ 5 };
constexpr int b{ 2 };
static_cast<double>(a) / b; //2.5추가로 0으로 나누게 되면 크래시가 발생한다 (수학적으로 정의되지 않기 때문)
이때 0.0으로 나누면 컴파일러나 아키텍처에 의해 값이 나오게 된다, IEEE754(부동소수점 표현, 연산 표준) 부동 소수점을 지원하면 NAN 혹은 Inf가 나오게 된다
산술 할당 연산자
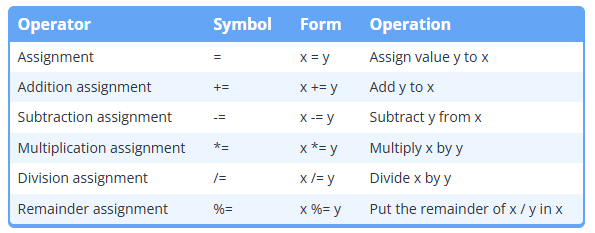
a += b;
a = a + b;위 두개의 표현식은 같다, 조금 더 편리하게 사용이 가능하다
나머지 연산자 %
보통 modulo operator라고 부르며 나머지를 반환하는 연산자이다
7 % 4; //3양수는 물론 음수에도 사용이 가능하다, 부호는 첫번째 피연산자의 부호를 따른다
-6 % 4 // -2
6 % -4 // 2원래 C++ 표준에서는 operator%는 이름이 없었다 하지만 C++20 표준에서는 modulo 연산자라고 불린다, 하지만 수학적으로 봤을때 -6 / 4의 나머지는 2지만 프로그래밍에서 -6 % 4는 -2이다, 따라서 remainder라고 명명하는게 더 맞는 방법일 수 있다
이러한 나머지 연산은 특정 연산에서 문제가 발생할 수 있다
(x % 2) == 1; //홀수 찾는 연산만약 x가 음수라면 -1이 나오기 때문에 이는 false가 된다, 따라서 홀수 짝수를 찾는 연산에서는 0과 비교하는게 좋다
지수 연산
수학에서 ^연산은 C++에서 존재하지 않는다, 따라서 다음과 같이 진행한다
#include <cmath>
std::pow(3.0, 2.0); //9std::pow()는 부동소수점을 사용하기 때문에 값이 100% 정확하다고 확신할 순 없다, 하지만 극도로 섬세한 프로그래밍이 아니라면 실사용에 크게 문제되지 않는다
이러한 pow()연산은 오버플로가 쉽게 발생할 수 있으니 조심해서 사용해야 한다
증감 연산자
증감 연산자는 ++, --가 존재하고 각각 1씩 더하고 뺀 결과를 반환한다
증감 연산자는 전위형, 후위형이 존재한다
(++a, a--)
int a { 1 };
++a; //2
--a; //1이때 후위형 증감 연산자는 피연산자의 사본을 생성하고 원본 피연산자의 값을 증가시킨다, 그리고 사본이 반환되고 사본이 증가된 후 사본은 삭제된다
int a{ 1 };
int b { a++ }; //1아주 미세하겠지만 전위형보다 성능이 떨어질 수 있다 (굳이 후위형을 쓸일이 아니라면 전위형으로 연산하는게 더 좋다)
쉼표 연산자
쉼표 연산자는 왼쪽 피연산자를 평가하고 오른쪽 피연산자를 평가한 뒤 오른쪽 피연산자의 결과를 반환한다
쉽게 설명하면 다음과 같다
a = (b, c); //a에는 c값이 들어가게 됨 a = b, c; //a에는 b값이 들어가고 c는 사라진다 (쉼표 연산자는 연산 우선순위가 가장 낮다) constexpr a{ 5 }, b{ 6 }; //이건 쉼표 연산자 아님조건 연산자
조건 연산자 ?는 3항 연산자이다 (피연산자 3개)
a ? b : c;a가 참이면 b, false면 c를 return한다
constexpr bool foo { true };
constexpr int a { foo ? 1 : 2 };조건 연산자를 사용할 때는 연산자 우선순위를 잘 생각해야 한다
constexpr int x{ 2 };
std::cout << (x < 0) ? "negative" : "non-negative";위 결과는 non-negative가 출력될 것 같지만 0이 나오게 된다
std::cout << (x < 0) 이 먼저 실행되고 조건 연산자가 그 뒤에 실행되기 때문이다
따라서 ( )를 통해 잘 묶어주어야 한다
std::cout << ((x < 0) ? "negative" : "non-negative");조건연산자에서의 두번째와 세번째 피연산자의 타입은 동일해야 한다, 이때 암시적 형변환으로 가능한 타입들은 달라도 상관 없다 (ex) int <-> float, 하지만 signed, unsigned는 금지)
복잡한 표현식에서의 조건 연산자는 지양하는게 좋다 (가독성 저하)
관계 연산자, 부동소수점 비교

전부 수학적의미와 같다
결과는 전부 true, false로 return한다
조건식에서 조건을 작성할 때 bool변수라면 == true, == false는 쓰지 않고 bool변수만 작성하는게 좋다
(굳이 쓸 필요가 없음)
if(a == true) //X
if(!a) //O부동 소수점끼리의 비교연산은 위험한 연산이 될 수 있다
constexpr double d1 { 100.0 - 99.99 };
constexpr double d2 { 10.0 - 9.99 };이 둘은 수학적으로 봤을때 0.01로 같다고 생각할 수 있지만 프로그래밍에서 그렇지 않다

실수는 항상 근사값이기 때문에 비교연산에서 의도치 않은 결과가 발생할 수 있다
따라서 ==, !=으로 비교하는건 지양한다
std::cout << std::boolalpha << (0.3 == 0.2 + 0.1); // false그렇다면 실수끼리의 == 비교 연산은 어떤 방식으로 하면 좋을까?
epsilon을 이용한 실수의 비교 연산
실수의 오차가 존재하기 때문에 실수끼리의 연산은 두 숫자가 거의 같은지를 확인하는것이다
epsilon이란 실수와 실수 사이의 가장 작은 차이를 의미한다
코드를 작성하며 살펴보자
constexpr double a{ 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 };
constexpr double b{ 1.0 };이 두값을 무작정 비교하면 false가 나오게 된다
우리는 epsilon을 이용하여 아주 미세한 차이면 같다라고 판단하는 로직을 작성해야 한다
#include <algorithm> // for std::max
#include <cmath> // for std::abs
bool approximatelyEqualRel(double a, double b, double relEpsilon)
{
return (std::abs(a - b) <= (std::max(std::abs(a), std::abs(b)) * relEpsilon));
}a와 b의 오차를 절대값으로 판단하고, a와 b 절대값 중 큰 값과 epsilon을 곱해준다, 이때 오차가 더 작으면 같다라고 판단한다
constexpr double a{ 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 };
constexpr double b{ 1.0 };
constexpr double relEps{ 1e-8 };
std::cout << std::boolalpha;
std::cout << approximatelyEqualRel(a, b, relEps) << std::endl;결과는 true로 나온다
하지만 훨씬 더 작은 수끼리의 비교로 미세한 오차가 발생한다면 이는 false를 반환할 것이다
따라서 더 작은 epsilon을 넘겨 오차의 절대값이 해당 epsilon보다 작으면 그냥 true로 반환해줘야 한다
bool approximatelyEqualAbsRel(double a, double b, double absEpsilon, double relEpsilon)
{
if (std::abs(a - b) <= absEpsilon)
return true;
return approximatelyEqualRel(a, b, relEpsilon);
}
int main()
{
constexpr double relEps{ 1e-8 };
constexpr double absEps{ 1e-12 };
std::cout << std::boolalpha;
std::cout << approximatelyEqualAbsRel(a, b, absEps, relEps) << std::endl;
}이런 방식으로 그나마 가장 정확한 실수끼리의 비교 연산이 가능해진다
논리 연산자

!는 true를 false로 false를 true로 변환한다
!은 굉장히 높은 연산자 우선 순위를 가진다
if (!x > y) //!x가 먼저 연산되고 > 가 나중에 연산된다따라서 ( )를 이용하여 잘 그룹화를 시키고 사용해야 한다
if (!(x > y))(A, B는 bool값 조건)
A && B는 A와 B가 둘 다 true여야 true이다 (둘 중 하나라도 false면 false)
if (value > 10 && value < 20)A || B는 A와 B 둘 중 하나라도 true면 true이다 (둘 다 false여야 false)
if (value == 0 || value == 1)이때 컴파일러는 &&에서 좌측 피연산자가 false일 경우 우측 피연산자는 계산하지 않고 바로 false를 return한다, 마찬가지로 ||에서도 좌측 피연산자가 true일 경우 우측 피연산자는 계산하지 않고 바로 true를 return한다 (최적화 목적, Short circuit evaluation)
이전장에서 설명한 피연산자의 평가 순서는 정해지지 않았다의 예외가 바로 이 ||와 &&이다
(C++ 표준에서 왼쪽부터 연산하도록 되어있음)
만약 &&, ||를 overloading하여 사용한다면 자동으로 이러한 최적화를 수행하지 않는다
또한 &&는 ||보다 우선순위가 높기때문에 둘을 함께 사용할때는 ( )를 잘 이용해야 한다
value1 || value2 && value3 //이 표현식은 value1 || (value2 && value3) 로 실행된다논리 xor
C++에서 논리 xor연산자는 존재하지 않는다
xor이란 A, B가 같으면 false, 다르면 true를 return한다

xor연산자가 따로 존재하진 않지만 operator!=를 사용하면 같은 결과를 얻을 수 있다
a != b; //a,b가 같으면 false 다르면 true이다대체 연산자
위에 정리한 &&, ||, !은 대체 연산자가 존재한다
(and, or, not)
하지만 이러한 이름을 사용하는건 지양한다
