[백준11657_자바스크립트(javascript)] - 타임머신

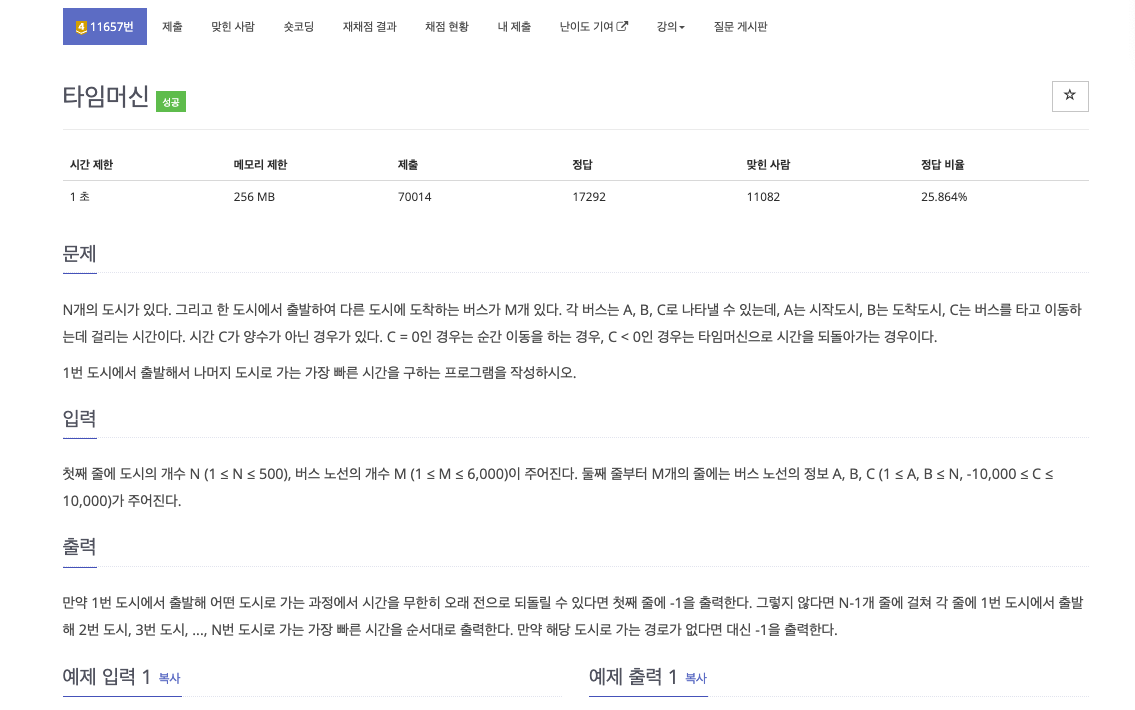
🔴 문제

타임머신

🟡 Sol

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const [[n, k], ...inputs] = fs
  .readFileSync(path)
  .toString()
  .trim()
  .split('\n')
  .map((it) => it.split(' ').map(Number));

const distance = Array(n + 1).fill(Infinity);

distance[1] = 0;

let hasNegativeCycle = false;
for (let i = 1; i <= n; i++) {
  for (const [a, b, c] of inputs) {
    if (distance[a] !== Infinity && distance[b] > distance[a] + c) {
      distance[b] = distance[a] + c;

      if (i === n) hasNegativeCycle = true;
    }
  }
}

if (hasNegativeCycle) console.log(-1);
else {
  for (let i = 2; i <= n; i++) {
    console.log(distance[i] === Infinity ? -1 : distance[i]);
  }
}

🟢 풀이

⏰ 소요한 시간 : -

1번 도시에서부터 모든 도시로 가는 최단 거리를 구하는 문제다. 다만 버스를 타고 이동하는 시간 C가 음수일 수도 있다. 따라서 벨만-포드 알고리즘으로 풀이한다.

거리 배열을 만들어준 뒤 1부터 n까지 모든 노드에서 모든 간선정보를 탐색하는데 방문한 적이 있어 거리 배열이 무한이 아니고, 최단거리가 갱신되는 경우 최단거리를 수정해준다. 만약 i가 n인데도 조건문에 걸리면 음수사이클이 존재해 최단거리가 무한이 갱신된다는 의미이므로, 해당 경우 hasNegativeCycle 변수를 true로 변경해 트리거해준다.

그 후 만약 hasNegativeCycle 변수가 참이라면 음수 사이클이 존재하므로 -1을 출력하고 변수가 거짓이라면 2부터 n까지 순회하면서 각 노드까지의 최단거리를 출력해준다. 이 때 각 노드의 값이 Infinity라면 1번노드로부터 도달하지 못하는 노드이므로 -1을 출력해준다.

🔵 Ref