[백준12865_자바스크립트(javascript)] - 평범한 배낭

🔴 문제

평범한 배낭

🟡 Sol

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const inputs = fs
  .readFileSync(path)
  .toString()
  .trim()
  .split('\n')
  .map((it) => it.split(' ').map(Number));
const [n, k] = inputs.shift();
const dp = Array.from({ length: n + 1 }, () => Array(k + 1).fill(0));
const W = [0];
const V = [0];

for (const [w, v] of inputs) {
  W.push(w);
  V.push(v);
}

for (let i = 1; i <= n; i++) {
  for (let j = 1; j <= k; j++) {
    if (j - W[i] < 0) dp[i][j] = dp[i - 1][j];
    else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
  }
}

console.log(dp[n][k]);

}

🟢 풀이

⏰ 소요한 시간 : -

DP유형 중 냅색 유형이다.
용량이 정해진 가방안에 넣을 수 있는 물건들의 최대 가치를 구하는 문제다.
접근 방향은 결국 물건을 넣거나, 안넣거나 둘 중의 한 가지를 택하면 되는 거니까 2차원 배열은 다음과 같이 만들 수 있다.

dp[i][j] -> i번째 물건을 넣었을 때 물건을 j만큼 채울 수 있을 때의 최대 가치

조금 어려울 수 있는데 예를 들어보자..!

위와 같이 행을 물건의 인덱스로 잡아 i번째 물건을 포함하거나 안포함하는 경우의 수 중 최대 값을 넣어주면 된다.
만약 i번째 물건을 넣는다면 가방 안에 최소 i번째 물건이 들어갈 공간이 있어야 한다. 따라서 현재 공간(무게)를 나타내는 열에서 현재 물건의 무게인 W[i]를 빼준 dp[i][j-W[i]]의 가치에서 현재 물건 가치 V[i]를 더해주면 현재 물건 i를 j공간에 놓었을 때의 최대 가치가 나오게 된다.
만약 i번째 물건을 넣지않는다면 가방에 아무런 일이 벌어지지 않으므로 dp[i-1][j]의 가치와 동일하게 된다.

그래서 중첩 반복문은 각각 1부터 n까지, 1부터 k까지 돌게 된다.

• 무게 6, 가치 13인 첫 번째 물건으로 반복문을 돌리고 나면 다음과 같아 진다.
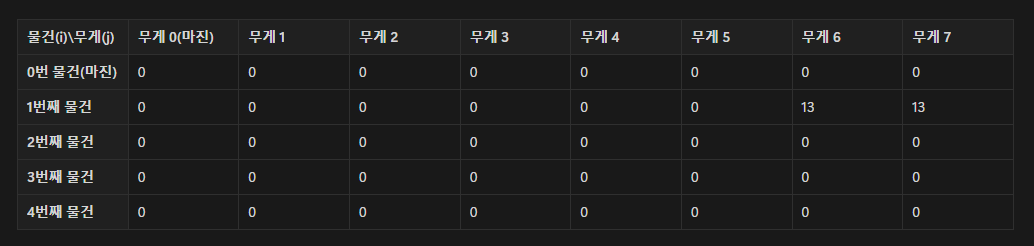
  무게 6인 물건을 넣으려면 최소 가방에 6 이상의 공간이 필요하기 때문에 j가 6, 7인 공간에만 물건을 넣어줄 수 있다.

   else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);

  이 물건은 0~5까지의 공간에 못들어 가기 때문에 조건처리를 해준다.

   if (j - W[i] < 0) dp[i][j] = dp[i - 1][j];

• 무게 4, 가치 8인 두 번째 물건으로 반복문을 돌리고 나면 다음과 같아 진다.
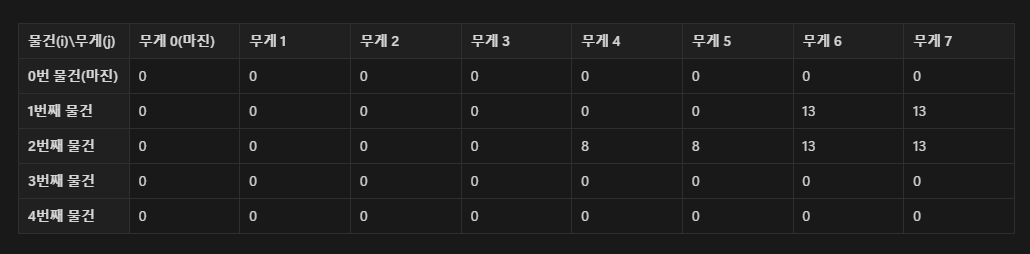
  무게 4인 물건을 넣으려면 최소 가방에 4 이상의 공간(남은 공간)이 필요하기 때문에 j가 6, 7인 공간에만 물건을 넣어줄 수 있다.

이와 같은 방식으로 2차원 dp배열을 다 채워주면 아래와 같은 배열이 나오고 우리는 dp[n][k]째의 값을 출력해주면 된다.

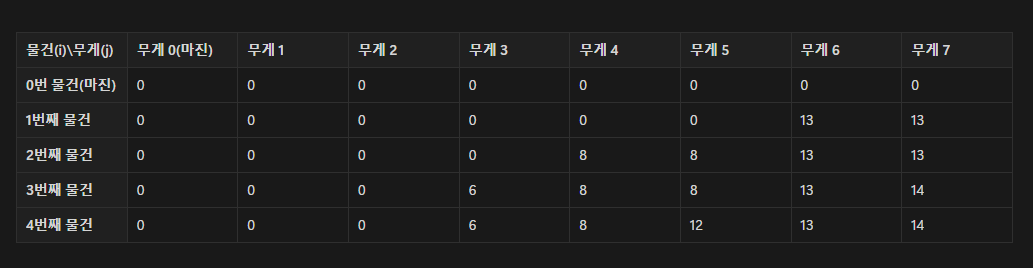
냅색 기본 유형은 위처럼 2차원으로 풀이하는 것이 기본이다.
여기서 조금 더 응용을 해보면 1차원으로 풀이할 수 있다.

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const [[n, k], ...inputs] = fs
  .readFileSync(path)
  .toString()
  .trim()
  .split('\n')
  .map((line) => line.split(' ').map(Number));
const dp = Array(k + 1).fill(0);

for (let i = 0; i < n; i++) {
  const [w, v] = inputs[i];

  for (let j = k + 1; j >= w; j--) {
    dp[j] = Math.max(dp[j], dp[j - w] + v);
  }
}

console.log(dp[k]);

이 dp[n]은 가방 안에 n만큼의 물건을 채울 수 있을 때 최대가치를 의미한다.
그래서 물건들을 순회하면서 물건의 개수인 n만큼 확인을 해줄 것이다.
이 때 내가 넣을 물건의 무게를 w, 가치를 v라고 하자.
이제 dp배열을 채워줄텐데 앞에서부터 채우는 것이 아니라 뒤에서부터 채워준다
왜냐하면! 앞에서부터 채웠을 때 내가 이미 현재 물건을 가방안에 넣었는데, 다음 dp에서 넣은 물건을 중복으로 또 넣을 수 있기 때문이다.
따라서 k+1의 가치일 경우부터 물건에 못넣게 되는 경우인 w까지 감소하면서 dp배열을 채워주면 중복을 방지할 수 있고 2차원 배열을 사용할 필요가 없어빈다.

🔵 Ref

https://www.youtube.com/watch?v=rhda6lR5kyQ
https://www.youtube.com/watch?v=XZjKsOVryls