[백준1300_자바스크립트(javascript)] - K번째 수

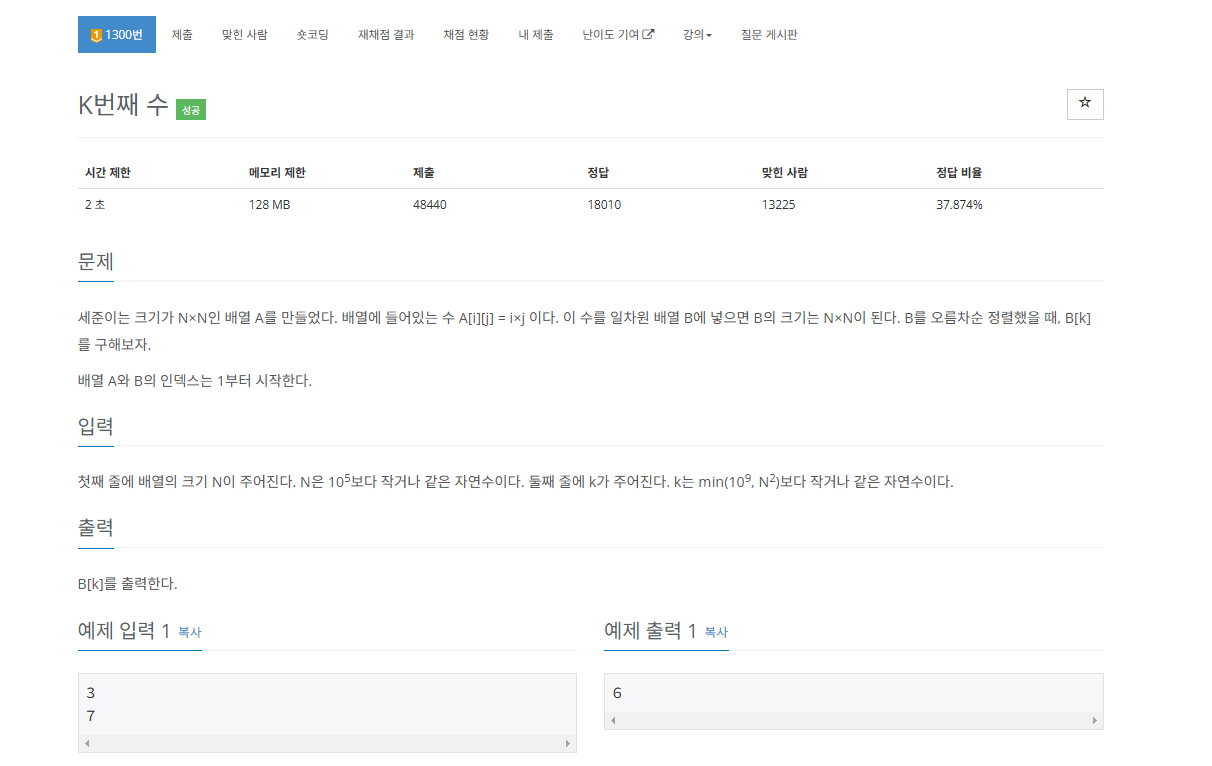
🔴 문제

K번째 수

🟡 Sol

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const [n, k] = fs.readFileSync(path).toString().trim().split('\n').map(Number);

let left = 1;
let right = k;
let ans = 0;
while (left <= right) {
  const mid = Math.floor((left + right) / 2);
  let cnt = 0;

  for (let i = 1; i <= n; i++) {
    cnt += Math.min(Math.floor(mid / i), n);
  }

  if (cnt < k) left = mid + 1;
  else {
    ans = mid;
    right = mid - 1;
  }
}

console.log(ans);

🟢 풀이

⏰ 소요한 시간 : -

완전탐색밖에 경우의수가 떠오르지 않아서 풀이를 봤다.
이분탐색인데 이분탐색임을 떠올리기 쉽지 않다...
아무튼 어떻게 풀이하냐면 정답이 될 수 있는 값은 무조건 k보다 작을 수 밖에 없다.

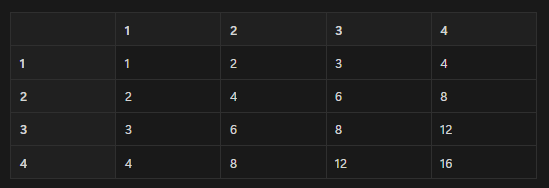
왜냐하면, 배열을 채워나가다 보면 2 두번 3은 두번 4는 세번씩 나오기 때문에 k보다 큰 값이 나올 수가 없다. 따라서 정답이 될 수 있는 최소값 1을 left로, 최대값 k를 right로 두고 이분탐색을 진행한다.
중앙값 mid를 구해준 뒤 1부터 n까지 모든 행을 순회한다. 그 후 각 열에 mid보다 작은 수가 몇개인지 판단해야 한다.

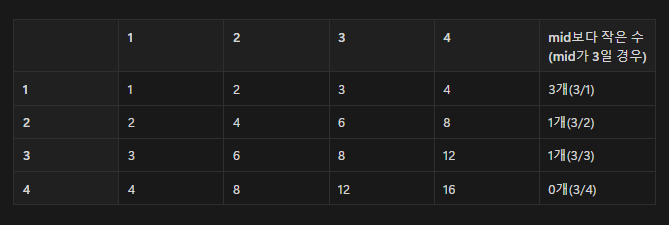
mid보다 작은 수가 몇 개인지 판단하려면 i로 나누어 주면 된다.(왜인지는 모르겠으나 위 사진을 보면 저런 식이 나오긴 함)
만약 mid/i가 n보다 클 경우에는?
해당 열에서 n보다 작은 수가 n개인 것이므로 모든 배열을 순회하며 mid보다 작은 수의 개수는 다음과 같이 구할 수 있다.

for (let i = 1; i <= n; i++) {
    cnt += Math.min(Math.floor(mid / i), n);
}

그 후 개수에 따라 left와 right의 값을 바꿔가며 정답을 찾아주면 된다.

앞으로 탐색을 모두 해야되는데 n이 크면 이분탐색을 떠올려 봐야겠다.

🔵 Ref