🔴 문제
🟡 Sol
const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const inputs = fs.readFileSync(path).toString().trim().split('\n');
const [n, m, k] = inputs[0].split(' ').map(Number);
const numbers = inputs.slice(1, n + 1).map(BigInt);
const queries = inputs.slice(n + 1).map((it) => it.split(' ').map(Number));
const tree = Array(n * 4).fill(0n);
const init = (start, end, node) => {
if (start === end) return (tree[node] = numbers[start]);
const mid = Math.floor((start + end) / 2);
return (tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1));
};
const update = (start, end, node, idx, diff) => {
if (start > idx || idx > end) return;
tree[node] += diff;
if (start === end) return;
const mid = Math.floor((start + end) / 2);
update(start, mid, node * 2, idx, diff);
update(mid + 1, end, node * 2 + 1, idx, diff);
};
const sum = (start, end, node, left, right) => {
if (start > right || left > end) return 0n;
if (left <= start && end <= right) return tree[node];
const mid = Math.floor((start + end) / 2);
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
};
init(0, n - 1, 1);
for (const [a, b, c] of queries) {
if (a === 1) {
const diff = BigInt(c) - numbers[b - 1];
numbers[b - 1] = BigInt(c);
update(0, n - 1, 1, b - 1, diff);
} else console.log(sum(0, n - 1, 1, b - 1, c - 1).toString());
}🟢 풀이
⏰ 소요한 시간 : -
총 N개의 수에서 구간합을 구하는 문제다. 입력으로는 k줄에 걸쳐 명령(query)가 주어진다.
각 쿼리는 세 정수 a, b, c로 구성되어 있고
a === 1이면 b번째 수를 c로 바꿈a === 2이면 b번째부터 c번째의 합을 구하는 문제이다.
이 때 n의 범위는 1,000,000이다. 구간합을 구하는 명령(a가 2인경우)마다 구간합을 단순 반복문으로 구하면 O(구간합 명령의 개수 * 구간) 즉 O(K*N) 의 시간이 소요되게 된다.
이 문제를 세그먼트트리라는 자료구조를 도입해 풀이하면 모든 쿼리를 O(logN)에 처리할 수 있다.
세그먼트트리는 모든 구간 각각의 합을 트리 형태로 저장해두고 수를 변경하는 쿼리를 수행할 때, 그 수가 포함되어있는 노드를 갱신하는 방식이다.
코드를 통해 알아보자
const numbers = inputs.slice(1, n + 1).map(BigInt);
const queries = inputs.slice(n + 1).map((it) => it.split(' ').map(Number));
const tree = Array(n * 4).fill(0n);numbers와 queries는 문제에서 주어진 숫자들과 쿼리들이다.
주목할 부분은 tree인데, n*4의 크기만큼 1차원 배열을 만들어 준다.
왜 n*4의 크기를 가질까 ?
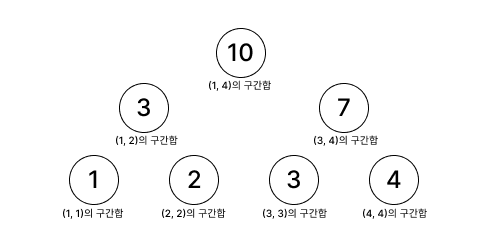위 구조는 N이 4일때의 세그먼트트리 기본구조다.
수열이 트리의 리프노드로 들어가고, 부모 노드로 올라가면서 구간합을 채우는 이진트리 구조다.
만약 N이 5라고 가정해보자
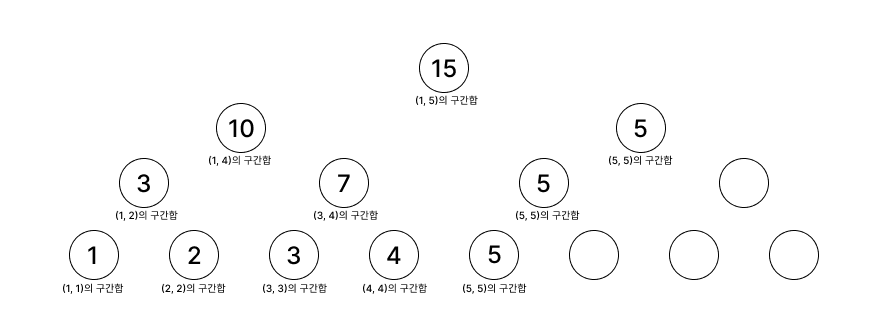노드는 하나가 증가했을 뿐인데, 트리의 높이는 1 증가하게 되고, 2^3승인 노드 8개가 더 추가됐다.
세그먼트 트리는 기본적으로 완전 이진 트리이기 때문에, 리프노드가 2의 거듭제곱이 되지 않으면, 가장 가까운 2의 거듭제곱까지 노드를 추가해야된다.
이런 구조적 특성을 바탕으로 총 노드의 개수를 수식화 하면 2 * 2^ceil(log₂N)의 노드의 개수를 가지게 되고 이를 간략하게 4N으로 표현하는 것이다.
각 노드들은 최상위루트노드부터 리프노드까지 1차원의 tree 배열에 저장된다. 어떻게 최상위노드부터 리프노드까지 데이터를 저장하는지 확인해보자!
트리 초기화 함수
다음은 위의 사진처럼 구간합을 배열로 초기화 하는 함수다.
const init = (start, end, node) => {
if (start === end) return (tree[node] = numbers[start]);
const mid = Math.floor((start + end) / 2);
return (tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1));
};init 함수는 세 개의 파라미터를 받는다.
start: 구간 시작 인덱스end: 구간 끝 인덱스node:start부터end까지의 구간합을 저장할 트리 배열 인덱스
init함수는 처음에 다음과 같이 호출되어 재귀적으로 값을 초기화한다.
init(0, n - 1, 1)첫번째수부터, n번째 수를 초기화하고 이 값은 1번째 자리에 초기화 해준다는 의미이다.
n개의 수를 절반으로 나눠 리프노드에 도달할 때 까지 재귀호출 해준다. 리프노드에 도달하면(start === end) 자기자신을 트리에 채워넣어주고 이 값을 리턴하며 재귀호출을 종료한다. 리턴값은 상위 호출로 전달되어 두 자식노드의 합이 부모노드에 저장되는 방식이다.
값 업데이트 함수
다음은 노드의 값을 변경시켜주는 함수다.
const update = (start, end, node, idx, diff) => {
if (start > idx || idx > end) return;
tree[node] += diff;
if (start === end) return;
const mid = Math.floor((start + end) / 2);
update(start, mid, node * 2, idx, diff);
update(mid + 1, end, node * 2 + 1, idx, diff);
};
`update함수는 다섯개의 파라미터를 받는다.
start: 구간 시작 인덱스end: 구간 끝 인덱스node:start부터end까지의 구간합을 저장할 트리 배열 인덱스idx: 업데이트를 할 원래 배열의 인덱스diff: 이전값과 변경될 값의 차이값
update함수는 다음과 같이 호출되어 재귀적으로 노드가 구간 내에 포함되어 있는 모든 노드의 합을 업데이트 해준다.
update(0, n - 1, 1, b - 1, diff);첫 번째부터 n번째까지 수의 구간합을 탐색할건데, b번째 인덱스가 포함되어 있으면 diff만큼 값을 더해주겠다라는 의미이다. 첫 번째 노드부터 n번째 노드까지의 구간합은 1번 인덱스에 위치하고 있으니 세번째 파라미터로 전달하는 node에는 1을 넣어준다.
내부적으로는 구간합의 시작 인덱스와 구간합의 끝 인덱스 안에 업데이트를 해줄 노드의 인덱스가 없으면 업데이트 해줄 필요 없으므로 탐색을 종료한다.
범위내라면 tree 배열에서 현재 노드를 diff 만큼 업데이트 해준다.
값을 변경해준 뒤 시작 인덱스와 끝 인덱스가 같다면 리프노드에 도착한 것 이므로 탐색을 종료한다.
리프노드가 아니라면 init함수처럼 절반씩 나누어서 업데이트 해주면 된다.
합 구하기 함수
다음은 합을 구해주는 함수다.
const sum = (start, end, node, left, right) => {
if (start > right || left > end) return 0n;
if (left <= start && end <= right) return tree[node];
const mid = Math.floor((start + end) / 2);
return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
};
sum함수는 다섯개의 파라미터를 받는다.
start: 구간 시작 인덱스end: 구간 끝 인덱스node:start부터end까지의 구간합을 저장할 트리 배열 인덱스left: 구하고자 하는 구간의 시작 인덱스right: 구하고자 하는 구간의 시작 인덱스
이 함수는 다음과 같이 호출된다.
sum(0, n - 1, 1, b - 1, c - 1)첫 번째부터 n번째까지 수의 구간합을 탐색할건데, b번째 수부터 c번째 수의 합을 구할 예정이다 라는 의미이다. 마찬가지로 최상위루트노드부터 탐색해야 하므로 세번째 인자로는 1을 넣어준다.
그런데 이런 구간합은 tree에 저장되어 있는데 왜 sum 함수가 필요할까 ?
이런 세그먼트 트리에서 1부터 3까지의 구간합을 구한다고 가정해보자
이 경우 1부터 2까지의 구간합 3과, 3부터 3까지의 구간합 3의 합처럼 여러 노드의 값을 합쳐야 한다. sum 함수는 은 이를 재귀적으로 합쳐준다.
그래서 sum 함수 내부에서는 범위에 완전히 벗어나면 0을 리턴,
범위에 완전히 포함되어 있으면 트리에서 현재 노드의 값을 리턴하면 된다. 그 이후로는 이전과 동일하게 절반씩 나누어서 재귀호출을 진행해주면 된다.
마지막으로 입력된 쿼리에 맞게 업데이트나 합계 함수를 호출해 원하는 결과를 얻으면 된다.
이 문제의 정답의 최대값은 2^63-1일 수 있다고 하니 모든 수는 BigInt로 다루도록 하자.
🔵 Ref
