[백준5719_자바스크립트(javascript)] - 거의 최단 경로

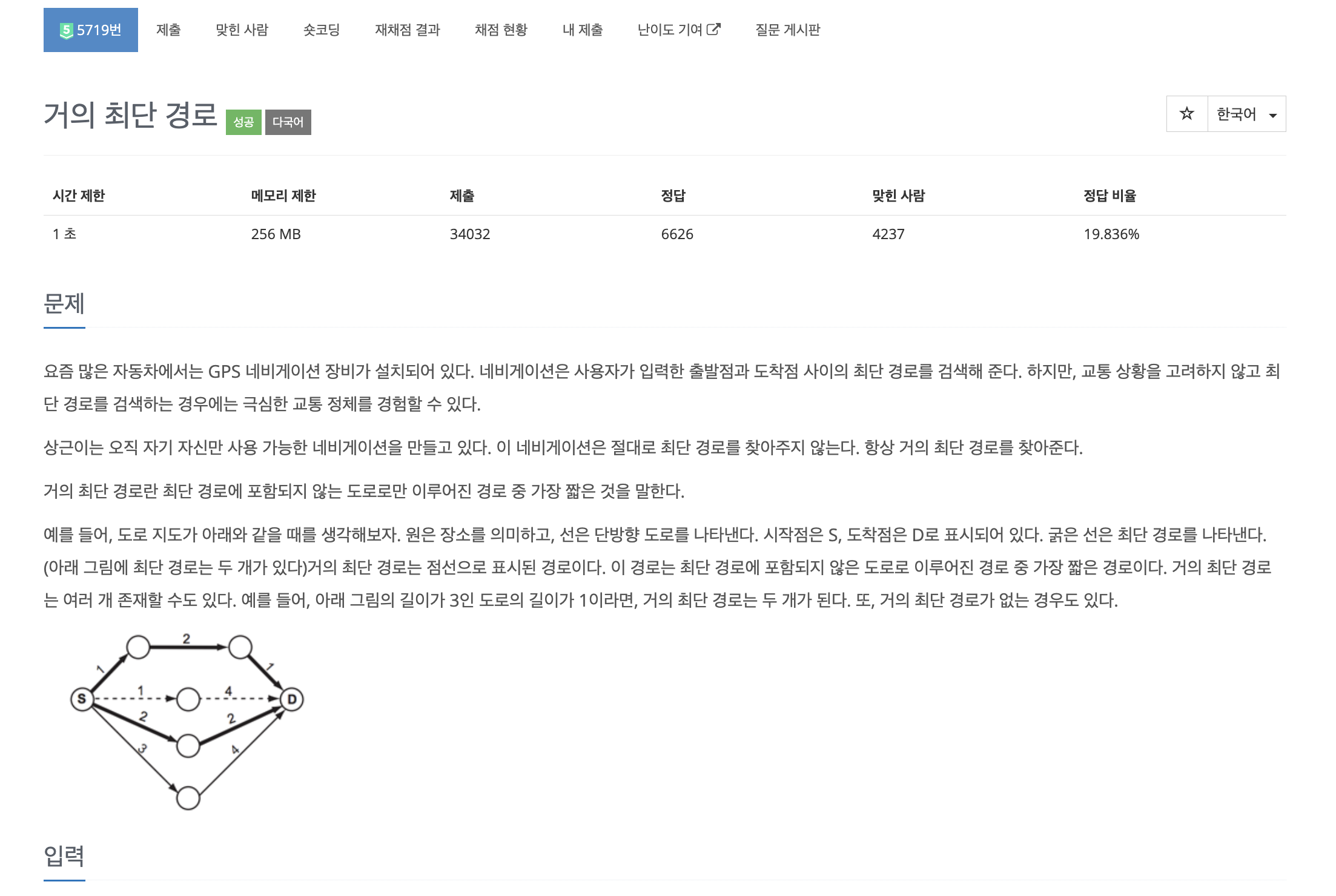
🔴 문제

거의 최단 경로

🟡 Sol

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const inputs = fs
  .readFileSync(path)
  .toString()
  .trim()
  .split('\n')
  .map((it) => it.split(' ').map(Number));
let front = 0;

const getMinNode = (n, distance, visited) => {
  let minNode = -1;
  let minDistance = Infinity;

  for (let i = 0; i < n; i++) {
    if (!visited[i] && distance[i] < minDistance) {
      minNode = i;
      minDistance = distance[i];
    }
  }

  return minNode;
};

const dijkstra = (s, n, graph) => {
  const parents = Array.from({ length: n }, () => new Set());
  const distance = Array(n).fill(Infinity);
  const visited = Array(n).fill(false);
  distance[s] = 0;

  for (let _ = 0; _ < n; _++) {
    const node = getMinNode(n, distance, visited);

    if (node === -1) break;
    visited[node] = true;

    for (const [next, cost] of graph[node]) {
      if (cost === -1) continue;

      if (distance[next] > distance[node] + cost) {
        distance[next] = distance[node] + cost;
        parents[next] = new Set([node]);
      } else if (distance[next] === distance[node] + cost) {
        parents[next].add(node);
      }
    }
  }

  return { distance, parents };
};

const removeEdge = (e, parents, graph) => {
  const q = [e];
  const visited = Array(graph.length).fill(false);
  visited[e] = true;
  let front = 0;

  while (front < q.length) {
    const node = q[front++];

    for (const parent of parents[node]) {
      graph[parent] = graph[parent].map(([next, cost]) => (next === node ? [next, -1] : [next, cost]));
      if (!visited[parent]) {
        visited[parent] = true;
        q.push(parent);
      }
    }
  }
};

while (front < inputs.length - 1) {
  const [n, m] = inputs[front++];
  const [s, e] = inputs[front++];
  const graph = Array.from({ length: n }, () => []);

  for (let _ = 0; _ < m; _++) {
    const [u, v, p] = inputs[front++];

    graph[u].push([v, p]);
  }

  const { distance, parents } = dijkstra(s, n, graph);

  if (distance[e] === Infinity) {
    console.log(-1);
    continue;
  }

  removeEdge(e, parents, graph);

  const { distance: ansDistance, _ } = dijkstra(s, n, graph);
  console.log(ansDistance[e] === Infinity ? -1 : ansDistance[e]);
}

🟢 풀이

⏰ 소요한 시간 : -

이 문제는 두번째 최단경로를 구하는 문제로 다익스트라와 bfs를 사용해 풀이할 수 있다.

풀이 방식은 다음과같다.

• 다익스트라를 사용해 최단경로를 구해준다.
• 최단경로를 구하면서 현재 최단경로의 직전 노드도 같이 구해준다.
• 구한 직전노드를 가지고 BFS 수행하면서 최단경로에 포함된 간선을 제거
• 제거한 뒤 다시 다익스트라를 통해 최단경로를 구함

자세히 살펴보자

먼저 여러개의 테스트 케이스가 주어지기 때문에 front변수 + while을 통해 입출력을 처리해준다. 단방향 그래프이므로 graph[u]와 연결된 노드 v를 가중치 p와 묶어서 저장한다.

그 후 다익스트라를 수행하는데, 다익스트라를 통해 시작위치 s로부터 모든 정점으로 가는 최단 경로를 구할 수 있다.
다익스트라는 visited와 getMinNode함수를 통해 방문하지 않은 노드 중 가중치가 가장 작은 노드를 탐색해서 disitance배열을 업데이트 시켜주면 된다.
distance배열을 업데이트 할 때, parents배열도 업데이트해야한다. 현재 경로를 선택했을 때 직전노드가 뭐였는지를 Set이라는 자료구조에 넣어준다. 만약 distance가 같은경우는 Set에 직전 노드를 추가한다.
다익스트라는 distance와 parents를 리턴하고, 리턴된 parents를 통해 bfs를 수행하며 최단경로 간선을 제거한다.

removeEdge함수는 도착노드 E에서부터 bfs를 수행한다.
bfs를 수행하면서 현재 노드와 연결된 노드들을 탐색하는데, 연결된 노드가 최단경로에 포함되어 있다면 기존 graph에서 코스트 정보를 -1로 바꿔준다.

그 후 다시 다익스트라를 수행해서 최단경로를 새로 구해주면 된다.

참고로 최단경로와 거의 최단경로 둘 다 없을 수도 있다.
이 경우 -1을 출력할 수 있도록 조건처리 한다.

🔵 Ref