[백준7869_자바스크립트(javascript)] - 두 원

🔴 문제

두 원

🟡 Sol

const fs = require('fs');
const path = process.platform === 'linux' ? '/dev/stdin' : 'input.txt';
const [x1, y1, r1, x2, y2, r2] = fs.readFileSync(path).toString().trim().split(' ').map(Number);
const d = Math.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2);

let ans;
if (r1 + r2 < d) ans = 0;
else if (d <= Math.abs(r1 - r2)) ans = Math.PI * Math.min(r1, r2) ** 2;
else {
  const c1 = 2 * Math.acos((r1 ** 2 + d ** 2 - r2 ** 2) / (2 * r1 * d));
  const c2 = 2 * Math.acos((r2 ** 2 + d ** 2 - r1 ** 2) / (2 * r2 * d));

  const part1 = 0.5 * r1 ** 2 * (c1 - Math.sin(c1));
  const part2 = 0.5 * r2 ** 2 * (c2 - Math.sin(c2));

  ans = part1 + part2;
}

console.log(ans.toFixed(3));

🟢 풀이

⏰ 소요한 시간 : -

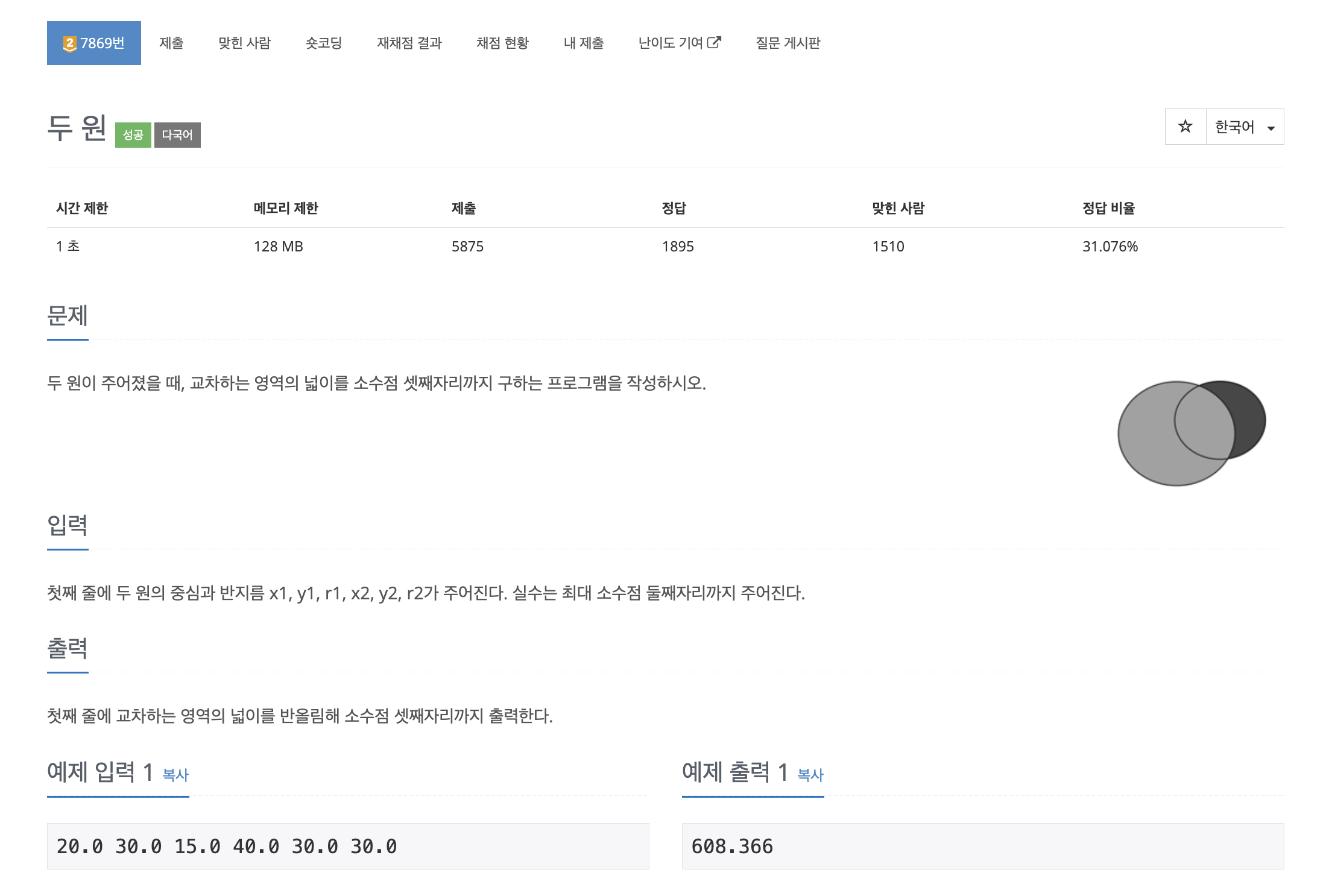
두 원의 겹치는 부분을 구하는 문제다.
구현은 어렵지 않지만, 수학적 지식으로 접근하는것이 상당히 어려운 문제
먼저 두 원의 중신 사이의 거리 d를 구해놓고 세 경우로 문제를 나눠서 풀이했다.

1. 두 원이 겹치지 않을 경우
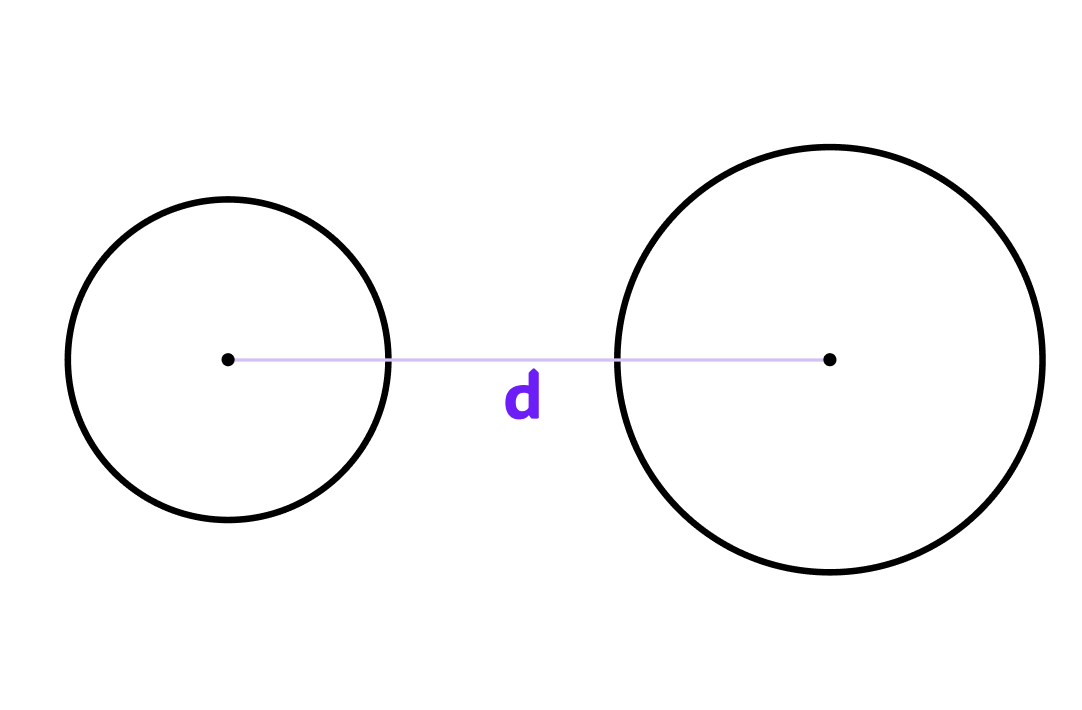두 반지름의 합보다 중심 거리 d가 더 큰 경우 원의 교집합 넓이는 0이 된다.

2. 두 원중 한 원이 다른 원에 완전히 포함 된 경우
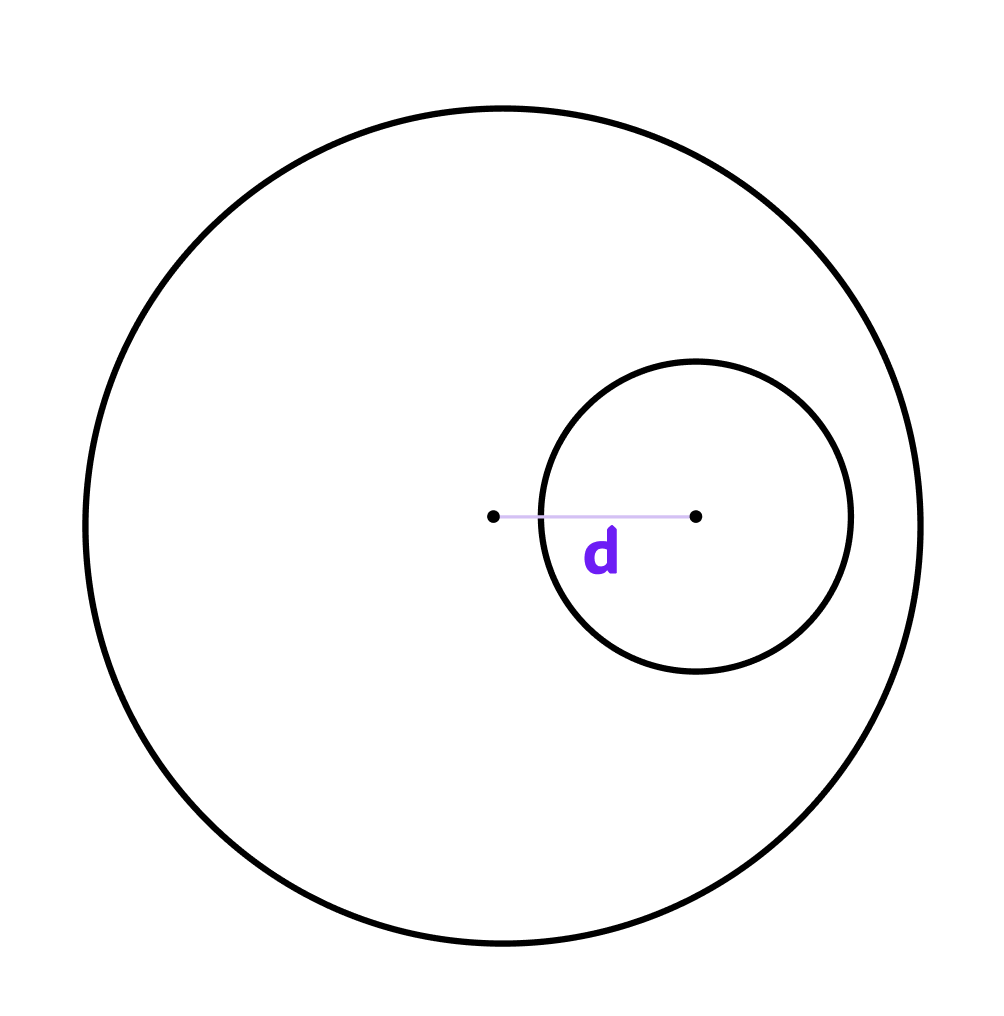이 경우는 d가 두 반지름의 차이보다 작거나 같은 경우다. 둘 중 작은원의 넓이가 교집합 넓이가 된다.

3. 두 원이 부분적으로 겹치는 경우
위의 두가지 경우를 제외하면 남은 경우는 두 원이 부분적으로 겹치는 경우뿐이다.
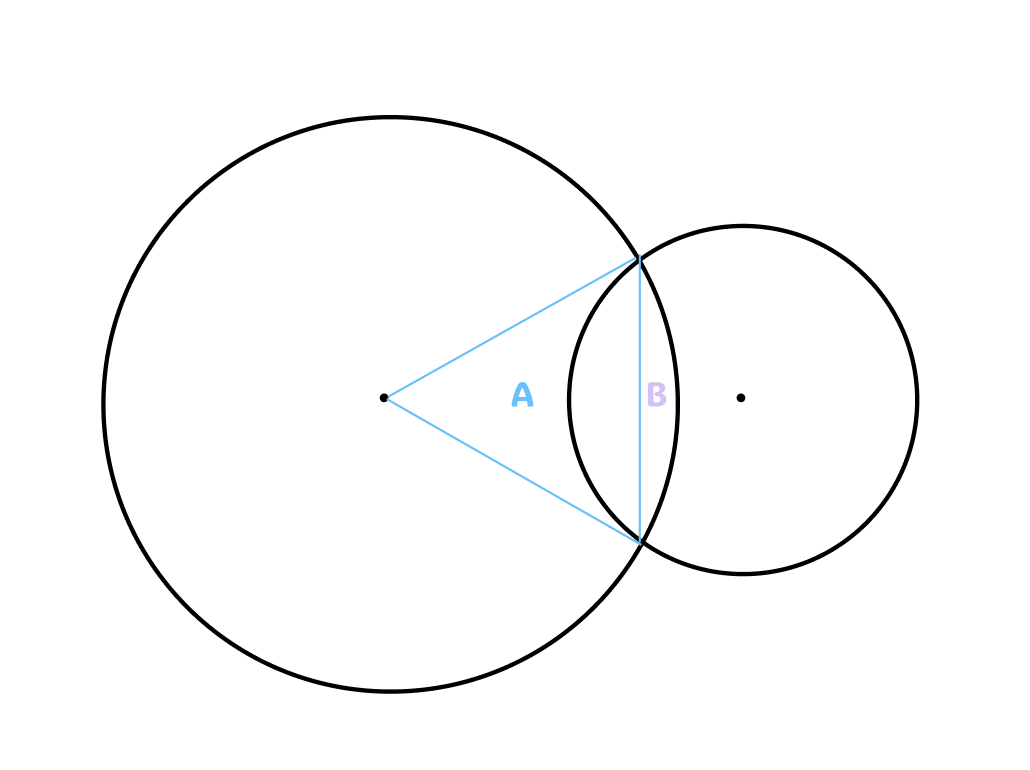
이 경우가 핵심인데, 겹치는 부분의 절반을 각각 구한 뒤 합쳐서 겹치는 부분을 구한다.
겹치는 부분의 반쪽(B)은 부채꼴 면적(A+B) - 삼각형 면적(A)을 통해 구할 수 있다.

이 때 삼각함수 공식을 사용하는데 자세한 내용은 수학적으로 더 설명이 잘되어 있는 블로그들을 참고하길 바란다...

🔵 Ref

https://loosie.tistory.com/778