
우리가 프로그램을 작성한 후에 실행하면 작업이 완료될때까지 어느정도 시간이 소요된다.
아주 간단한 프로그램인 경우에는 실행 시간을 걱정할 필요가 없지만,
처리하는 데이터가 많아지고 처리하는 작업이 복잡해질수록 실행 시간은 매우 중요해진다.
이번 포스팅은 특정 알고리즘을 작성하였을 때 그 실행 시간을 표기하는 방법에 대한 내용이다.
1. Big O
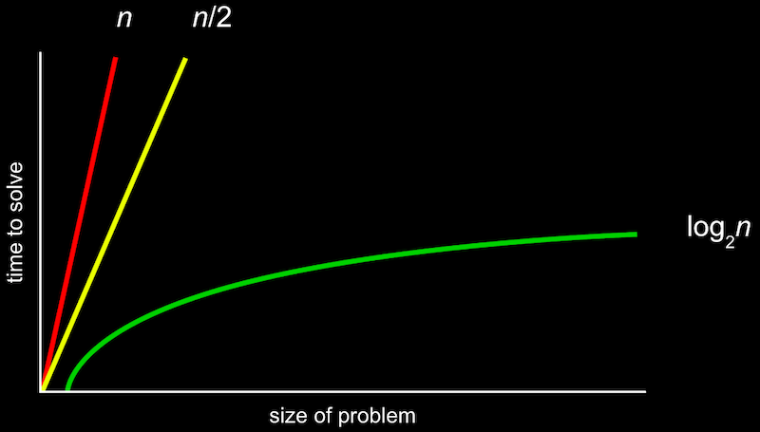
위와 같은 그림을 공식으로 표기한 것이 Big O 표기법이다.
여기서 O는 “on the order of”의 약자로, 쉽게 생각하면
“~만큼의 정도로 커지는” 것이라고 볼 수 있다.
O(n) 은 n만큼 커지는 것이므로 n이 늘어날수록 선형적으로 증가하게 된다.
O(n/2)도 결국 n이 매우 커지면 1/2은 큰 의미가 없어지므로 O(n)이라고 볼 수 있다.
주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용된다.
- O(n^2)
- O(n log n)
- O(n) - 선형 검색
- O(log n) - 이진 검색
- O(1)
(여기에 더 상세한 설명, 예시와 그래프가 있으므로 참고)
2. Big Ω
Big O가 알고리즘 실행 시간의 상한을 나타낸 것이라면,
반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타내는 것이다.
예를 들어 선형 검색에서는 n개의 항목이 있을때 최대 n번의 검색을 해야 하므로
상한이 O(n)이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 Ω(1)이 된다.
역시 아래 목록과 같은 Big Ω 표기가 많이 사용된다.
- Ω(n^2)
- Ω(n log n)
- Ω(n) - 배열 안에 존재하는 값의 개수 세기
- Ω(log n)
- Ω(1) - 선형 검색, 이진 검색
생각해보기
Q. 실행시간의 상한이 낮은 알고리즘이 더 좋을까요, 하한이 낮은 알고리즘이 더 좋을까요?
A.
우선 나는 실행시간의 상한이 낮은 알고리즘이 더 좋다고 생각한다.
이유는 쉽게 예를 들어 설명보겠다.
예전에 내가 올렸던 게시물 중에 숫자야구 게임이라는 것이 있었다.
1) 실행시간의 상한이 낮은 알고리즘
실행시간의 상한:24
여기서 처음에 1234를 입력했는데 모두 ball이 나왔다고 가정해보자.
즉, 홈런에 1,2,3,4의 숫자가 모두 사용되며 자리수만 다른 경우이다.
다만 여기서 기존 룰과 다르게 실행 횟수에 제한이 없다는 룰을 추가해보자.
그럼 나는 경우의 수를 따져봤을 때 4 x 3 x 2 x 1 = 24번의 횟수 안에서
이 알고리즘을 끝낼 수 있다는 것을 예측할 수 있다.
이후 1234, 1243, 1324, 1342, 1423, 1432 식으로 자리수를 바꿔가며 홈런을 찾는 로직을
구현하여 프로그램을 실행시킬 수 있다.
2) 실행시간의 하한이 낮은 알고리즘
실행 시간의 하한:1 (즉, 최소 실행 횟수 1, 의미가 없다고 볼 수 있다.)
1)의 경우와 똑같이 1234가 모두 ball이 나온 상황이다.
그런데 여기서 1234를 랜덤으로 돌리는 로직을 구현하여(중복 입력 제외 기능 포함)
운좋게 2번만에 홈런을 맞췄다.
여기서 2)의 알고리즘이 1)의 알고리즘보다 더 좋다고 말할 수 있을까?
물론 이 경우 1)의 경우보다 홈런을 빠르게 맞췄지만 나는 2)의 경우가
예측이 불확실하다는 점에서 그다지 좋은 알고리즘은 아니라고 생각했다.
만약 홈런이 1432였다고 해보자.
1)의 경우 숫자 순으로 실행하며 6번만에 홈런을 맞출 수 있다.
하지만 2)의 경우 랜덤으로 돌리다보면 최악의 경우 24번만에 홈런을 맞출 수도 있는 것이다.
따라서 나는 실행시간의 상한이 낮은 알고리즘이며, 예측이 가능한 1)의 경우가
더 좋은 알고리즘이라 생각한다.
Ref.
- Edwith_boost course
- https://brenden.tistory.com/2
- https://noahlogs.tistory.com/27
- https://medium.com/@callmedevmomo/%EC%9B%B9-%EA%B0%9C%EB%B0%9C%EC%9E%90%EB%A5%BC-%EC%9C%84%ED%95%9C-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0%EC%99%80-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-01-%EB%B9%85%EC%98%A4-%ED%91%9C%EA%B8%B0%EB%B2%95-ff369f0efc1d