
1. 문자의 표현
컴퓨터는 문자를 숫자로 표현 할 수 있도록 정해진 약속(표준) 이 있다.
그 중 하나는 미국정보교환표준부호 ASCII(아스키코드/American Standard Code for Information Interchange) 이다.
총 128개의 부호로 정의되어 있는데, 가령 알파벳 A는 10진수 기준으로 65, 알파벳 B는 66으로 되어있다.

여기서, A를 2진법으로 표현한다면,
우선 10진법 기준으로 65이므로 2^6x1 + 2^5x0 + 2^4x0 + 2^3x0 + 2^2x0 + 2^1x0 + 2^0x1 = 64+1,
따라서 A를 2진법으로 표현하면 1000001이다.
이번엔 MOON을 2진법으로 표현한다면?
M: 2^6x1 + 2^5x0 + 2^4x0 + 2^3x1 + 2^2x1 + 2^1x0 + 2^0x1 = 64 + 8 + 4 + 1 = 77,
O: 2^6x1 + 2^5x0 + 2^4x0 + 2^3x1 + 2^2x1 + 2^1x1 + 2^0x1 = 64 + 8 + 4 + 2 + 1 = 79,
O: 2^6x1 + 2^5x0 + 2^4x0 + 2^3x1 + 2^2x1 + 2^1x1 + 2^0x1 = 64 + 8 + 4 + 2 + 1 = 79,
N: 2^6x1 + 2^5x0 + 2^4x0 + 2^3x1 + 2^2x1 + 2^1x1 + 2^0x1 = 64 + 8 + 4 + 2 = 78,
M: 1001101
O: 1001111
O: 1001111
N: 1001110
소문자도 ASCII에서 숫자로 나타낼 수 있다. 소문자 'a'는 숫자 97로 나타내고 'b'는 98로 나타내며 이 후 다른 소문자들도 마찬가지이다.
따라서 컴퓨터가 소문자 'a'를 저장하려면 숫자 97을 2진수, 1100001로 저장해야 한다.
소문자는 같은 대문자 글자보다 항상 2^5만큼 크다.
즉, 이진수에서 2^5의 자릿수만 바꾸면 소문자와 대문자 간의 변환을 쉽게 할 수 있다.
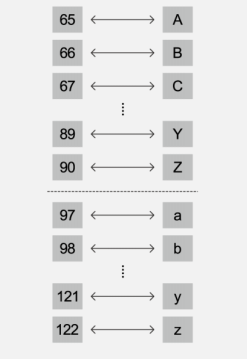
기본 ASCII 코드 표는 7비트만 이용해서 모든 문자들을 나타낸다.
즉, 2^7 = 128개의 문자를 나타낼 수 있다는 것을 의미한다.
확장 ASCII는 8번째 비트를 추가하여 총 256개의 문자를 나타낼 수 있도록 한다.
소문자와 대문자 통틀어 52개 알파벳 밖에 없으므로, 그 외 남는 공간에 구분 기호, 숫자, 몇몇 기본 심볼들($나 % 기호 등) 같은 다른 종류의 문자들을 나타낼 수 있다.
하지만 8비트 ASCII 코드로도 나타낼 수 없는 문자들이 아직도 많이 있다.
우리가 사용할 수 있는 문자들의 개수는 256개보다 많기 때문이다.
예를 들어, 수학 기호들과 영어 외 다른 언어의 글자들은 표준 ASCII 표에 들어가기 힘들다.
이 때문에 훨씬 더 많은 문자들을 포함할 수 있는 유니코드(Unicode)가 생기게 됐다.
예를 들어, 유니코드는 100만개 이상의 문자들을 나타낼 수 있는 문자 인코딩 표준이다.
유니코드의 첫 128개의 문자는 ASCII의 128개의 문자와 동일하므로 서로 호환이 된다.
Unicode는 😂(기쁨의 눈물) 이런 이모티콘 까지 표현할 수 있게 해주었다. 이 이모티콘은 10진법으로 128,514이다. 2진법으로는 11111011000000010 이다.
만약 우리가 스마트폰으로 😂(기쁨의 눈물) 이모티콘을 친구의 스마트폰으로 보낸다면 11111011000000010 이라는 0과 1의 패턴을 보낸것이다.
2. 그림, 영상, 음악의 표현
문자와 같이 그림도 역시 숫자로 표현할 수 있다.
우리가 스크린을 통해 보는 그림을 자세히 살펴 보면 수많은 작은 점들이 빨간색, 초록색, 파란색을 띄고 있다.
이런 작은 점을 픽셀이라고 부른다. 각각의 픽셀은 세 가지 색을 서로 다른 비율로 조합하여 특정한 색을 갖게 된다.
예를 들어 빨간색 72, 초록색 72, 파란색 33을 섞게 되면 노란색이 되는 것과 같은 방식이다.
이 숫자들을 표현하는 방식을 RGB(Red, Green, Blue)라고 한다.
즉, 노란색의 커다란 이미지는 72 73 33 으로 정의되는 무수히 많은 픽셀들의 RGB코드(숫자)로 표현할 수 있다.
영상 또한 수많은 그림을 빠르게 연속적으로 이어 붙여놓은 것이기 때문에 숫자로 표현이 가능하다.
음악도 마찬가지로 각 음표를 숫자로 표현할 수 있다.
Ref.
Edwith_boost course