개요

• 알고리즘의 성능을 수학적으로 표현해주는 표기법
• 알고리즘의 시간과 공간복잡도 표현 가능
• 알고리즘의 데이터 혹은 사용자의 증가율 예측을 목표로 한다

유형

O(1)

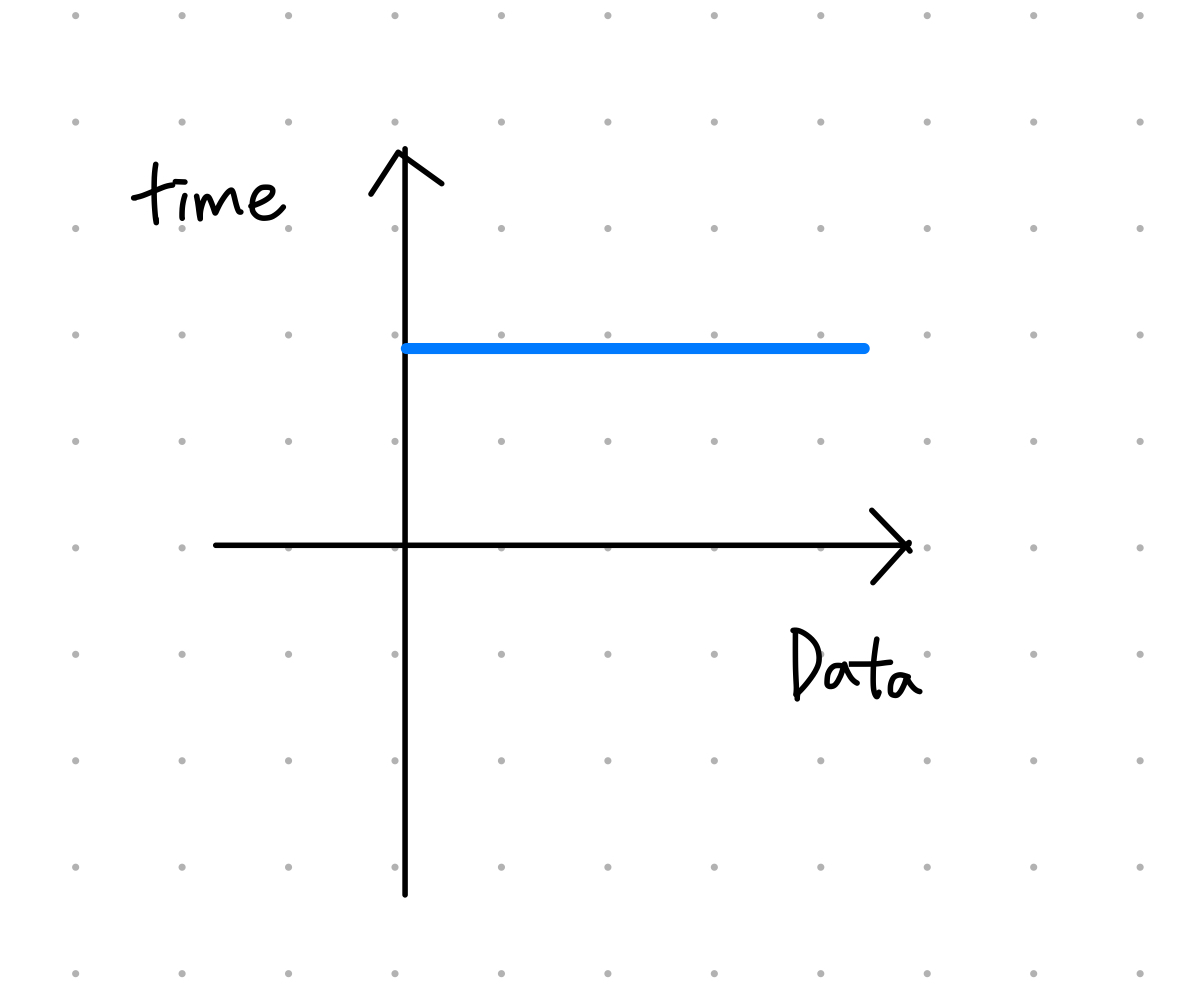
• 데이터가 증가해도 성능에 변화가 없음

code

let n = [];
function f() {
  return (n[0] === 0) ? true : false;
}

O(n)

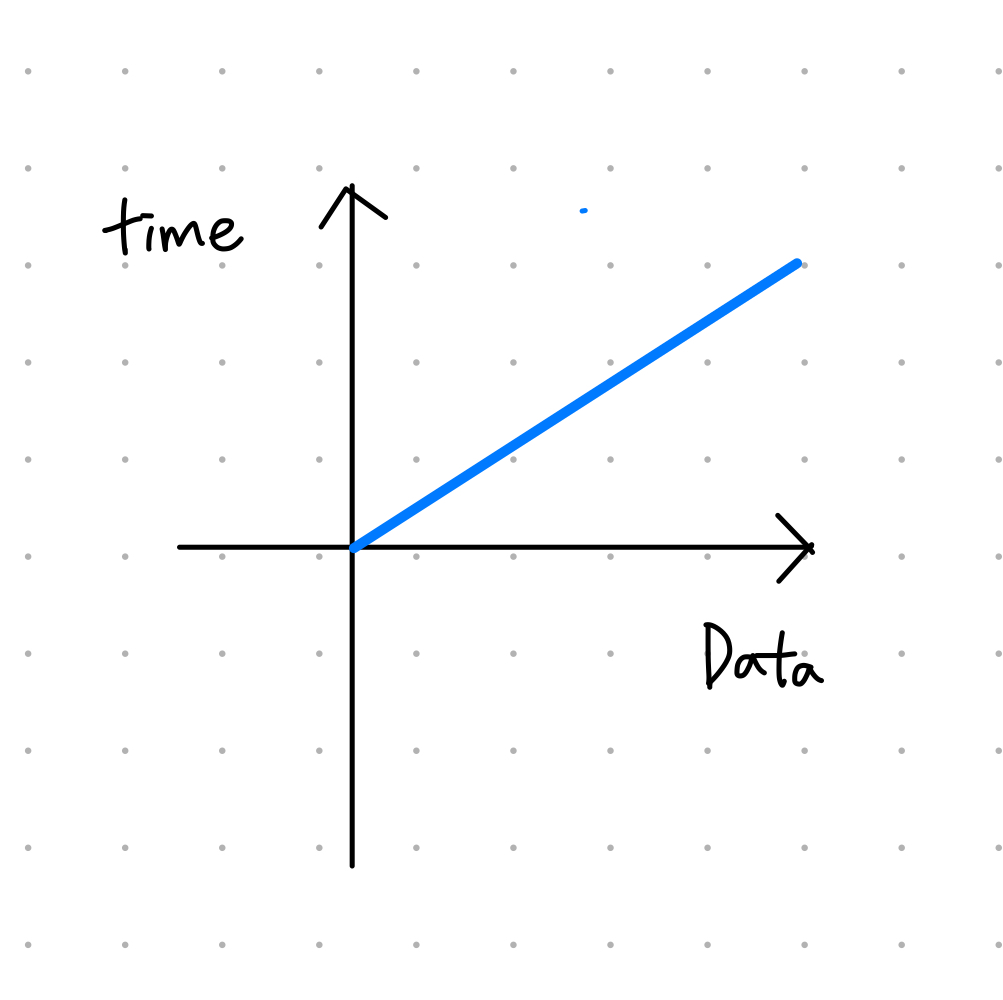
• 입력 데이터의 크기에 비례해 처리 시간이 걸리는 알고리즘

code

let n = [];
for(let i = 0; i < n.length; i++) {
	console.log(n[i]);
}

O(n²)

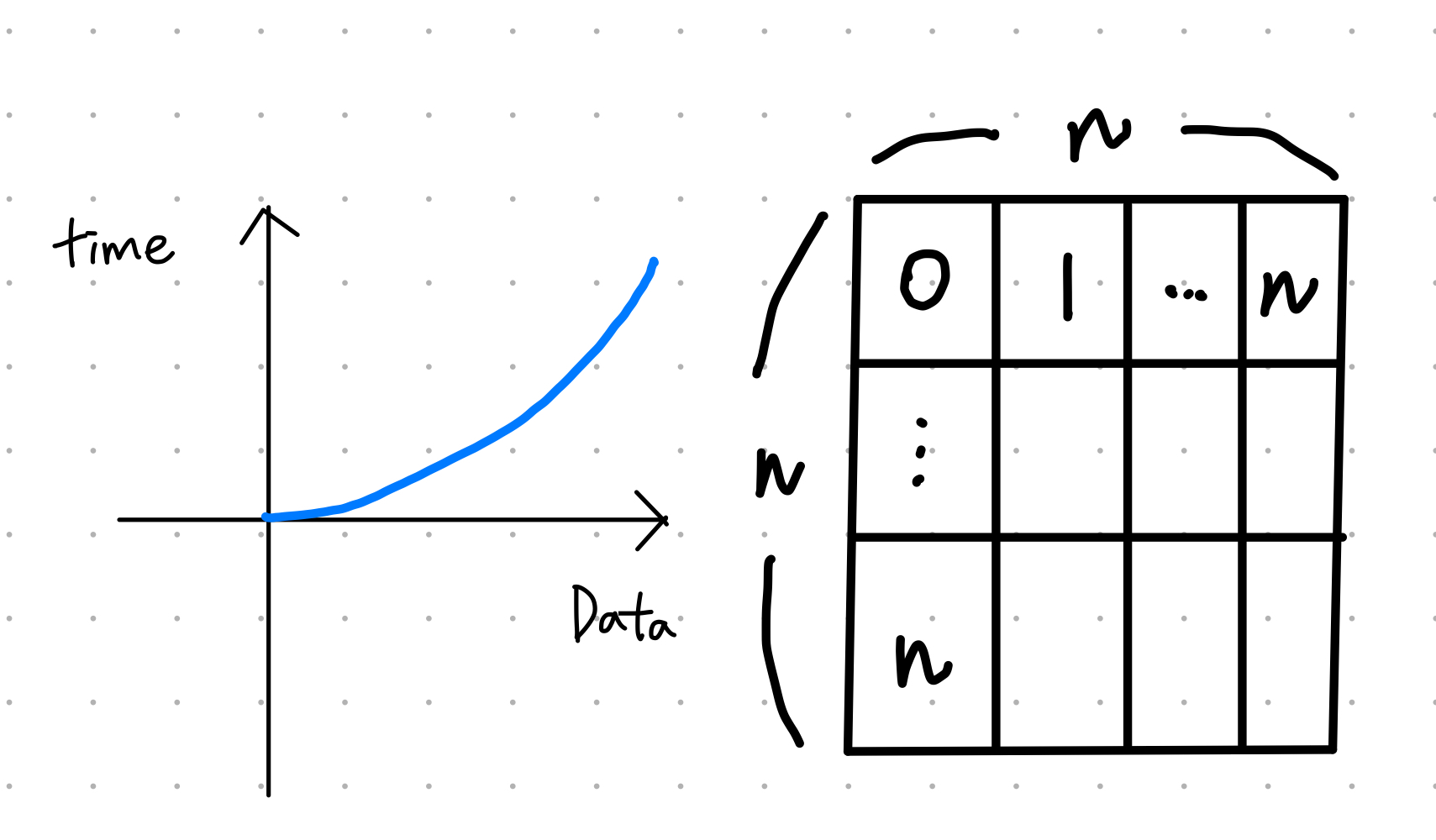
• n개의 데이터를 받으면 n번만큼 처리회수가 늘어난다
• 데이터가 n개만큼 커질수록 처리 시간이 늘어나고 부담이 커진다

Code

let n = [];
for(let i = 0; i < n.length; i++) {
    for(let j = 0; j < n.length; j++) {
      console.log(i + j);
    }
}

O(nm)

• n²와 비슷하다가 생각할 수 있지만 n²과 다르게 n을 n만큼 루프하는 것이 아닌 m을 n만큼 루프하는것이다

code

let n = [] 
let m = [];
for(let i=0; i<n.length; i++){
    for(let j=0; j<m.length; j++){
        console.log(i + j);
    }
}

O(n³)

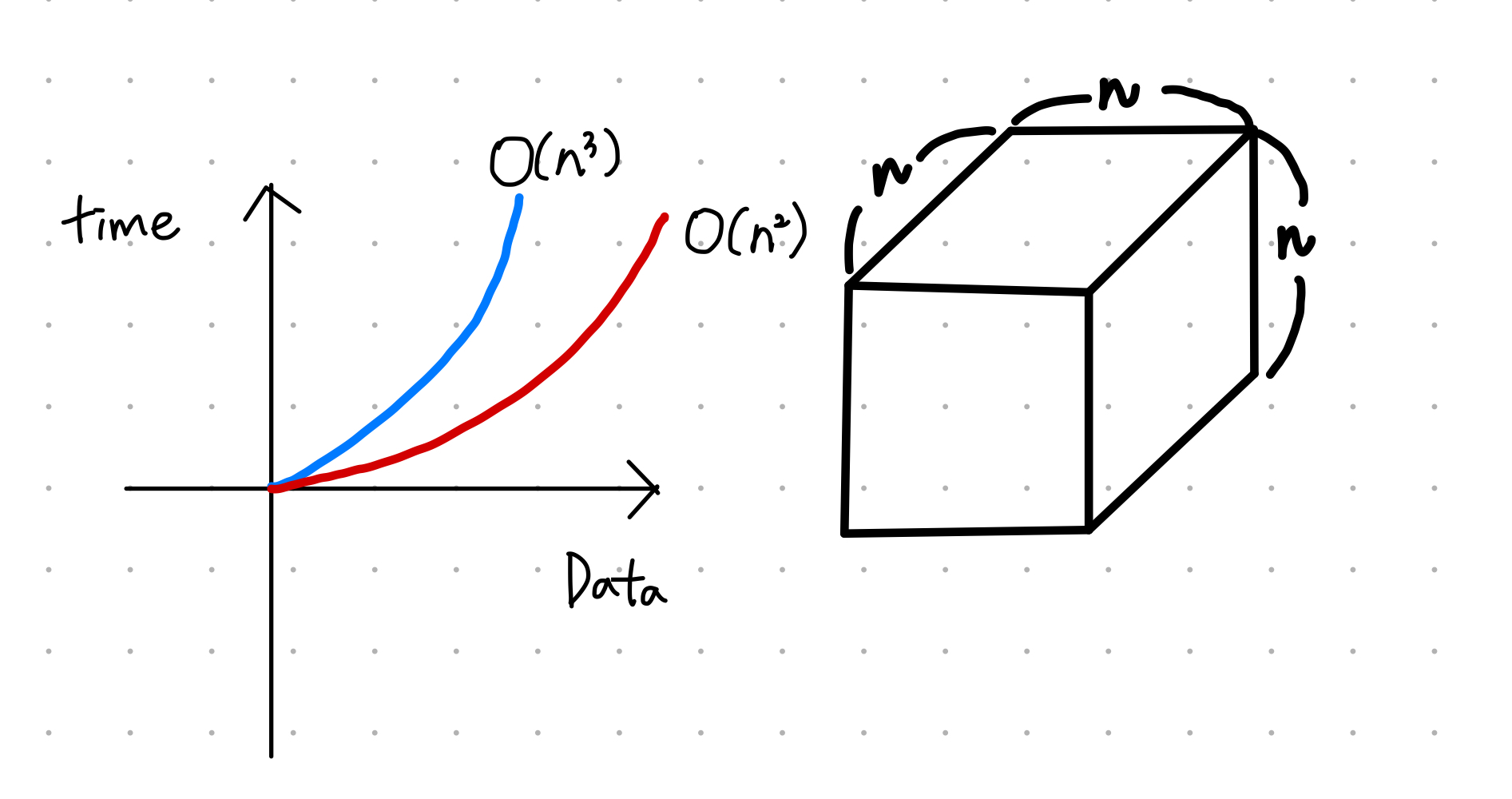
• n²을 n만큼 한번 더 루프한다. 3차원..?

code

let n = [];
for(let i = 0; i < n.length; i++) {
    for(let j = 0; j < n.length; j++) {
    	for(let k = 0; k < n.length; k++){
            console.log(i + j + k);
        }
    }
}

O(2^n)

• Fibonacci 수열과 같음

code

function f(n) {
    if(n <== 0) return 0;
    else if(n === 1) return 1;
    return f(n - 1) + f(n - 2);
};

O(log n)

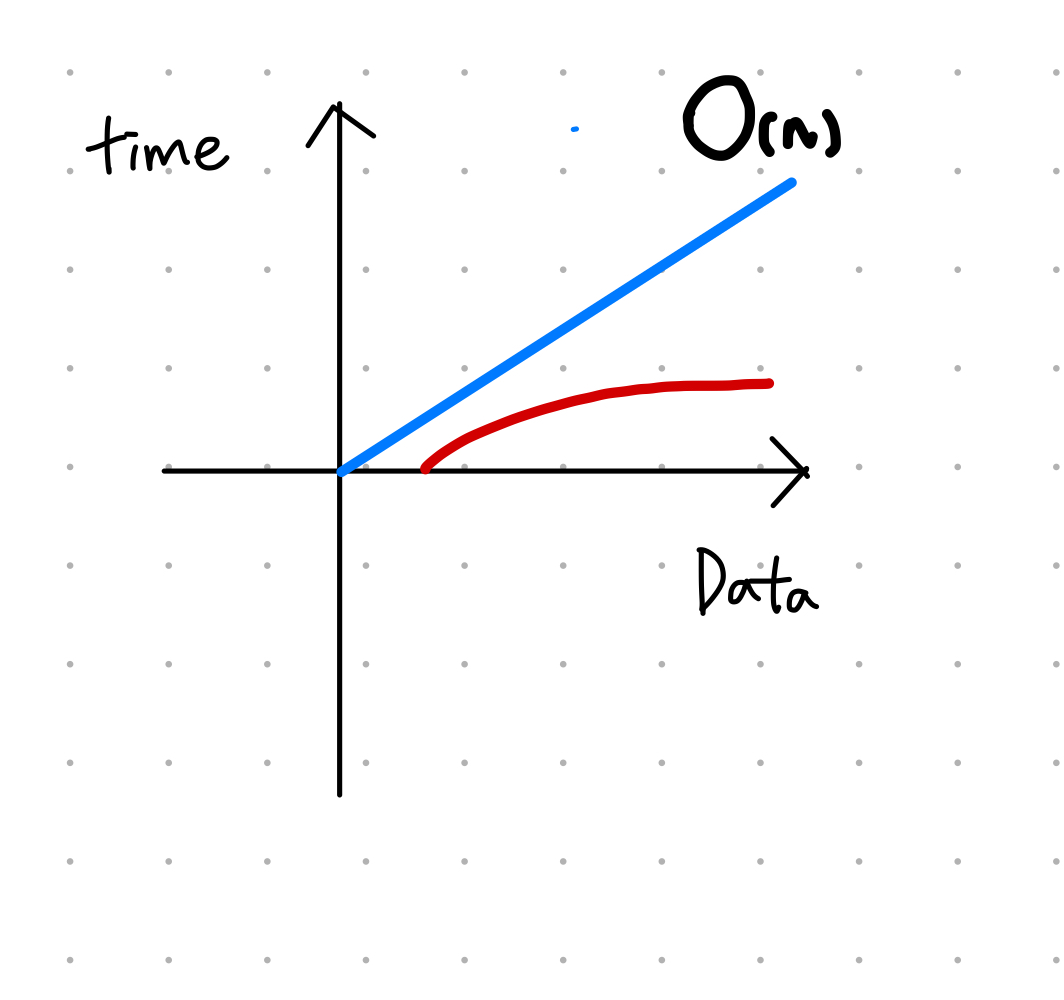
• 대표적인 알고리즘으로 이진검색이 있음
• 한번 함수가 호출될 때마다 중간값을 기준으로 절반은 검색영역에서 제외시키므로 순차 검색에 비해 속도가 훨씬 빠름

이건 이진탐색을 정리할 때, 코드를 첨부해야겠다.