개요

Tree는 이름처럼 나무가 뿌리를 내리는듯한 구조로 되어있다.
트리 중 가장 최상위에 위치한 Node를 Root Node라고 부른다.

function tree(value){
  this.value = value;
  this.children = [];
}

1. 이진트리

• 이진트리는 자식 노드가 왼쪽, 오른쪽 두개뿐인 트리이다.

function binaryTreeNode(value) {
  this.value = value;
  this.left = null;
  this.right = null;
}

function binaryTree(){
  this.root = null;
}

이진트리의 순회 방법

• 순회의 방법 기준은 root node(현재 node)의 기준점에 따라 순회 과정이 진행된다.

선순위 순회 (pre-order)

선순위 순회는 root(현재 node) -> 왼쪽 -> 오른쪽순으로 진행된다.

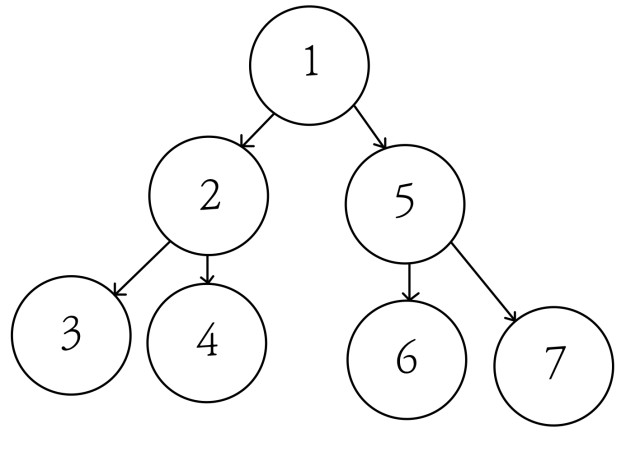
과정

1. root인 1번이 출력
2. 왼쪽 node 시작
3. root의 왼쪽에 위치한 node 2번 출력
4. 2번 node의 왼쪽에 위치한 node 3번 출력
5. 2번 node의 오른쪽에 위치한 node 4번 출력
6. 왼쪽 node 끝
7. 오른쪽 node 시작
8. root의 오른쪽에 위치한 node 5번 출력
9. 5번 node 왼쪽에 위치한 node 6번 출력
10. 5번 node 오른쪽에 위차한 node 7번 출력
11. 오른쪽 node 끝
12. 순회 완료

코드

function preOrderIteration(){
  // 빈 스택에 루트 추가
  let nodeStack = [];
  nodeStack.push(this.root);
  
  // 모든 항목 하나씩 출력
  while(nodeStack.length){
    // 스택 최상위 항목 꺼내서 출력
    let node = nodeStack.pop();
    
    // 꺼낸 노드의 오른쪽, 왼쪽 자식 노드를 스택에 추가
    if(node.right)
      nodeStack.push(node.right)
    if(node.left)
      nodeStack.push(node.left)
  }
}

중순위 순회 (in-order)

중순위 순회는 왼쪽 -> root(현재 node) -> 오른쪽순으로 진행된다.

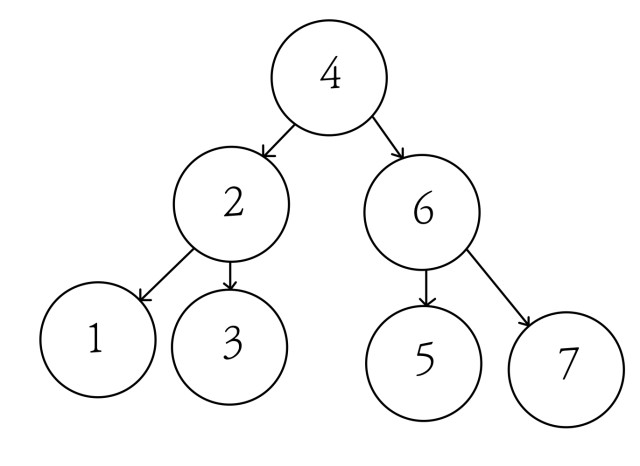
과정

1. 왼쪽 node 시작
2. 왼쪽인 1번이 출력
3. 1번 node의 root인 node 2번 출력
4. node 2번의 오른쪽 자식인 node 3번 출력
5. 왼쪽 node 끝
6. node 2번의 root인 node 4번 출력
7. 오른쪽 node 시작
8. 오른쪽 노드들의 왼쪽 node인 5번 출력
9. 5번 node의 root인 node 6번 출력
10. root node 5번의 오른쪽 자식 node인 7번 출력
11. 오른쪽 node 끝
12. 순회 완료

코드

function inOrderIterate(){
  let current = this.root;
  let s = [];
  let done = false;
  
  while(!done){
    if (current !== null) {
      s.push(current);
      current = current.left;
    } else {
      if (s.length) {
        current = s.pop();
        current = current.right;
      } else {
        done = true;
      }
    }
  }
}

후순위 순회 (post-order)

후순위 순회는 왼쪽 -> 오른쪽 -> root(현재(node)순으로 진행된다.

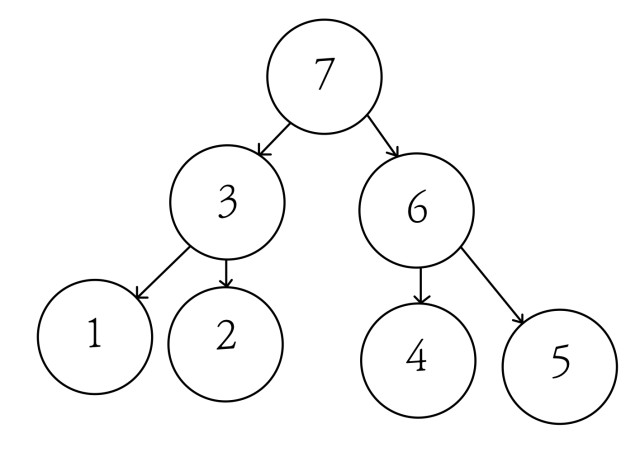
과정

1. 가장 최상위 node의 자식 node 중 왼쪽부터 시작
2. 왼쪽 node 시작
3. 3번 node의 자식 node 중 왼쪽 node인 1번 출력
4. 3번 node의 자식 node 중 오른쪽 node인 2번 출력
5. node 1번과 2번의 root인 3번 출력
6. 왼쪽 node 끝
7. 오른쪽 node 시작
8. 6번 node의 자식 node 중 왼쪽 node인 4번 출력
9. 6번 node의 자식 node 중 오른쪽 node인 5번 출력
10. node 4번과 5번의 root인 6번 출력
11. 오른쪽 node 끝
12. 가장 최상위 node 7번 출력
13. 순회 완료

코드

function postOrderIterate() {
  let s1 = [], s2 = [];
  s1.push(this.root);
  
  // 첫번째 스택 비울때까지 계속 실행
  while(s1.length){
    const node = s1.pop();
    s2.push(node);
    
    // 제거된 항목의 왼쪽과 오른쪽 자식노드를 s1에 추가
    if (node.left)
      s1.push(node.left);
    if (node.right)
      s1.push(node.right);
  }
  // 두번째 스택의 모든 항목 출력
  while(s2.length){
    const node = s2.pop();
  }
}

이진 tree 순회 선택 기준

• 자식 node가 없는 node에 접근하기 전에 root를 먼저 접근해야 하는 경우 선순위 순회를 선택하면 된다.
• 부모 node를 선택하기 전에 자식 node가 없는 node를 먼저 접근해야 하는 경우 후순위 순회를 선택하면 된다. 후순위 순회를 선택하면 root를 접근하는 시간 낭비를 하지 않기 때문이다.
• tree의 node 자체에 순서가 있어서 tree를 원래 순서대로 순회하고 싶을 때는 중순위 순회를 선택하면 된다.