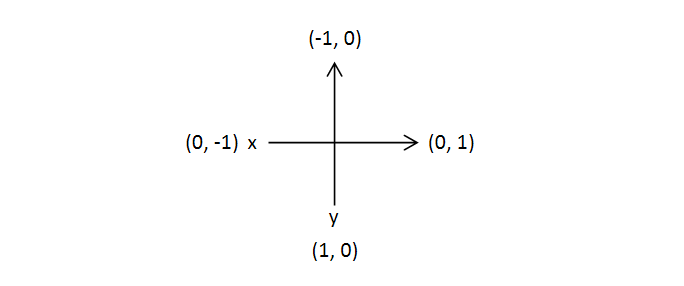Java 알고리즘 (업데이트: 2025.01.19.)

devyumi·2023년 12월 18일
알고리즘
0

Java

목록 보기
4/14

0. 기본

Queue

  • Queue는 인터페이스이기 때문에 하위 클래스로 구현함
// 생성
Queue<Integer> queue = new LinkedList<>();

offer() //추가
poll() // 반환 및 제거
peek() // 반환 (제거 X)

Priority Queue

  • 우선 순위 기준을 구현할 것

  • 구현하지 않을 경우 ClassCastException 발생

PriorityQueue<Edge> pQ = new PriorityQueue<>((o1, o2) -> o1.weight - o2.weight);

Graph

1) 인접 행렬: 2차원 배열

가) 생성

int[][] arr = new int[n][m];

2) 인접 리스트: 2차원 리스트

가) 생성

ArrayList<Integer>[] arr = new ArrayList[n + 1];

나) 각 행에 대한 리스트 생성

for(int i = 1; i < 10; i++){
	arr[i] = new ArrayList<>();
}

다) 리스트 타입에 2개 이상의 인스턴스가 사용된다면 내부 클래스를 만들어 사용해보자

// Queue에 x, y 좌표 값 넣기
// 내부 클래스 없을 때

Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
int[] now = q.poll();
        int x = now[0];
        int y = now[1];
// 내부 클래스 있을 때

Queue<Point> queue = new LinkedList<>();
        queue.add(new Point(x, y));
Point now = queue.poll();
int x = now.x;
int y = nox.y;

private static class Point {
	private int x, y;
	public Point(int x, int y) {
		this.x = x;
		this.y = y;
	}
}


1. 그리디

  • 현 상황에서 가장 좋아 보이는 것만을 선택하는 알고리즘


2. 구현

dx, dy 테크닉

  • 배열 dx, dy에 좌표를 설정하여 위치 이동할 수 있도록 함

    • if문으로 좌표를 옮기는 대신 사용하여 상, 하, 좌, 우를 쉽게 탐색할 수 있음
int[] dx = {-1, 1, 0, 0}; //상 하 좌 우
int[] dy = {0, 0, -1, 1};



3. 완전 탐색

DFS

  • 한 노드에서 방문하지 않은 노드 중 하나만 스택에 넣음
  • 재귀함수 사용

BFS

  • 한 노드에서 방문하지 않은 모든 노드를 큐에 넣음
  • 최단 경로 구하기
    -> BFS는 최단 거리를 찾으면 곧바로 종료 가능하여 DFS보다 더 효율적임

BackTracking

  • 가지치기하여 탐색할 수 있는 경우의 수를 줄임 (=막히면 돌아간다)
  • 노드가 해가 될 수 있는지 판단하고, 유망하지 않다고 결정되면 부모 노드로 돌아가 다음 자식 노드로 감
  • 중복이 없어야 한다면 visited 체크 필수
private static void backTracking(int depth) {
	if (depth == m) {	// 깊이가 조건과 같다면
		// 계산, 출력 등을 실행하고 재귀함수 하나를 빠져나감
		return;
	}

    for (int i = 1; i < m; i++) {
        if (!visited[i]) {		// 아직 방문하지 않았다면
            visited[i] = true;	// 방문처리를 하고
            arr[depth] = i;		// 값을 넣고
            backTracking(depth + 1);	// 다음 결과를 구하기 위해 재귀함수를 호출함 
            visited[i] = false;	// 재귀함수를 빠져나오면 방문처리 한 값을 원래대로 돌려놓음
        }
    }
}


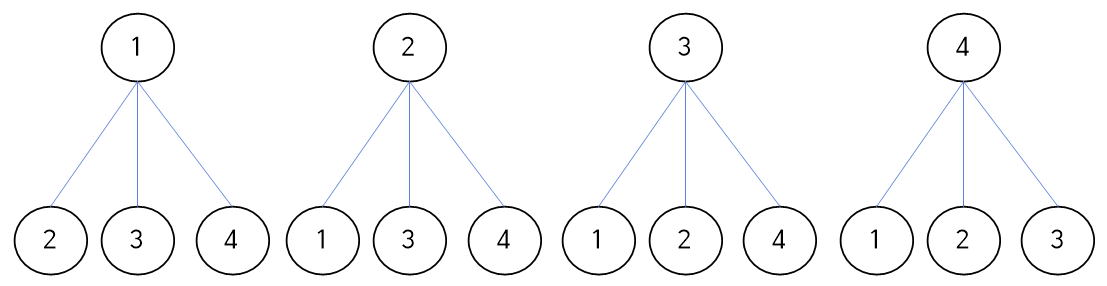
순열, 조합

예시) n = 4, r = 2

  • 순열: 서로 다른 n개에서 r개를 뽑아 정렬하는 경우의 수
    -> (1,2) (1,3) (1,4) (2,1) (2,3) (2,4) (3,1) (3,2) (3,4) (4,1) (4,2) (4,3)

  • 중복 순열: 서로 다른 n개에서 중복이 가능하게 r개를 뽑아 정렬하는 경우의 수
    -> 위 답안 + (1,1) (2,2) (3,3) (4,4)

  • 조합: 서로 다른 n개에서 순서 없이 r 개를 뽑는 경우의 수 (=부분집합)
    -> (1,2) (1,3) (1,4) (2,3) (2,4) (3,4)

  • 중복 조합: 서로 다른 n개에서 순서 없이, 중복이 가능하게 r개를 뽑는 경우의 수
    -> 위 답안 + (1,1) (2,2) (3,3) (4,4)


4. 정렬

  • 항상 어떤 순서로 정렬할 것인지 생각할 것

내림차순

// 오류: 참조형 배열 사용할 것
Arrays.sort(intArr, Collections.reverseOrder());

// 정상 작동: int[] -> 스트림 -> 참조형(boxed 사용) -> Integer[] 변환
Integer[] integers = Arrays.stream(intArr).boxed().toArray(Integer[]::new);
Arrays.sort(integers, Collections.reverseOrder());

cf) Wrapper 클래스

cf) 이중 콜론 연산자 (::)

  • '메서드, 생성자 참조 표현식'라고도 함
  • 람다식을 사용할 때, 파라미터 중복을 피하기 위해 사용함
  • 위 참조형 변환 코드를 람다식으로 표현하면 아래와 같이 구현할 수 있음
Integer[] integers = Arrays.stream(intArr).boxed().toArray(x -> new Integer[5]);

그 외

  • Comparator 사용하여 원하는 순서를 구현할 것
//예시: 각 요소의 2번째 문자를 기준으로 오름차순 정렬
String[] arr = {"paper", "light", "apple", "flower", "coffee"};

Arrays.sort(arr, new Comparator<String>() { //paper light flower coffee apple
	@Override
	public int compare(String o1, String o2) {
	return o1.charAt(1) - o2.charAt(1);
	}
});

5. 탐색

  • key 값과 배열 중간에 위치한 값을 반복 비교하여 데이터를 찾는 알고리즘

  • 간단해 보이지만 입력 값이 매우 크게 주어진 경우 사용 고려

binarySearch(int[] arr, int key) {
	int start = 0;
	int end = arr.length - 1;

	while(start <= end) {
		int mid = (start + end) / 2;
		if(arr[mid] == key) {	// 배열의 중간에 위치한 값과 key가 같으면 break
			return mid;
		} else if(arr[mid] < key) {		// key 값이 배열 중간에 위치한 값보다 크면 arr[mid]보다 큰 곳에서 key를 찾음
			start = mid + 1;
		} else {
			end = mid - 1;
		}
	}
	return -1;
}

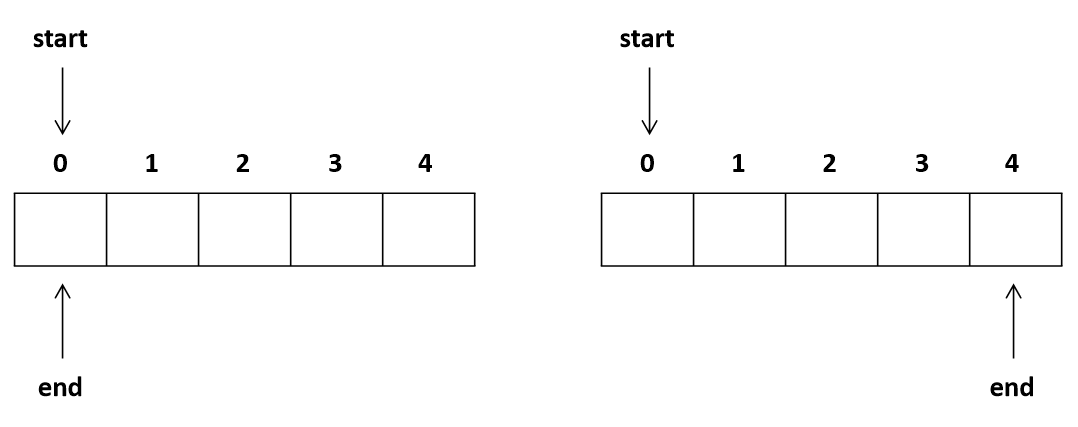
투포인터

  • start, end 두 개의 index 포인터를 사용하여 배열을 탐색하는 기법

  • 입력 값이 매우 크고 배열의 (연속되는) 특정 구간을 처리해야 할 때 사용 고려

  • 완전 탐색: O(n²) vs 투포인터: O(n)

// 맨 앞 start, 맨 뒤 end 시작
int start = 0;
int end = arr.length - 1;

while (start != end) {
	if (arr[start] + arr[end] == m) {
		answer++; // 계산 처리
		start++;
	} else if (arr[start] + arr[end] > m) {
		end--;
	} else {
		start++;
	}
}

// 맨 앞에서 start, end 시작
int start = 0;
int end = 0;
int sum = 0;

while (true) {
	if (sum >= m) {
		sum -= arr[start++];
	} else if (end == arr.length) {
		break;
	} else {
		sum += arr[end++];
	}

	if (sum == m) {
		answer++;
	}
}


LIS (가장 긴 증가하는 부분 수열)

1) 최장 길이 구하기

  • 실제 LIS 부분 수열을 구할 순 없음, 말 그대로 길이만 알 수 있음

방법 1: dp & 이중 for 문 -> O(n²)

public class Lis {
    public static void main(String[] args) {
        int[] arr = {40, 20, 30, 10, 15, 25, 30, 5};

        int[] dp = new int[arr.length];
        Arrays.fill(dp, 1);

        for (int i = 1; i < arr.length; i++) {
            for (int j = 0; j < i; j++) {
                if (arr[i] > arr[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
        }
    }
}

방법 2: binary search -> O(nlog n)
1) lis 배열 마지막 원소보다 key 값이 크면 lis 배열에 key 값을 추가함
2) lis 배열 마지막 원소보다 key 값이 작거나 같으면 이진탐색 시작

public class Lis { // 답: 4
    public static void main(String[] args) {
        int[] arr = {40, 20, 30, 10, 15, 25, 30, 5};
        int[] lis = new int[arr.length];
        int length = 0;

        lis[length++] = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (lis[length - 1] < arr[i]) {
                lis[length++] = arr[i];
            } else {
                int index = binarySearch(lis, arr[i], length);
                lis[index] = arr[i];
            }
        }
    }

    private static int binarySearch(int[] arr, int key, int end) {
        int start = 0;
        while (start <= end) {
            int mid = (start + end) / 2;
            if (arr[mid] == key) {
                return mid;
            } else if (arr[mid] > key) {
                end = mid - 1;
            } else {
                start = mid + 1;
            }
        }
        return start;
    }
}

2) 실제 LIS 수열 구하기

  • 최장 길이를 구하는 과정에서 배열의 각 원소가 Lis 배열 몇 번째 index에 들어갔는지 저장하는 result 배열을 만들 것
  • result 배열의 값을 역순으로 stack에 넣은 후 꺼낼 것
public class Lis { // 답: 10, 15, 25, 30
    public static void main(String[] args) {
        int[] arr = {40, 20, 30, 10, 15, 25, 30, 5};
        int[] lis = new int[arr.length];
        int[] result = new int[arr.length];
        int length = 0;

        lis[length++] = arr[0];
        result[0] = length;

        for (int i = 1; i < arr.length; i++) {
            if (lis[length - 1] < arr[i]) {
                lis[length++] = arr[i];
                result[i] = length;
            } else {
                int index = binarySearch(lis, arr[i], length);
                lis[index] = arr[i];
                result[i] = index + 1;
            }
        }

        Stack<Integer> stack = new Stack<>();
        for (int i = arr.length - 1; i >= 0; i--) {
            if (result[i] == length) {
                stack.push(arr[i]);
                length--;
            }
        }
	}
}


6. DP

  • 큰 문제를 작은 문제로 나눌 수 있고, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있을 때 사용

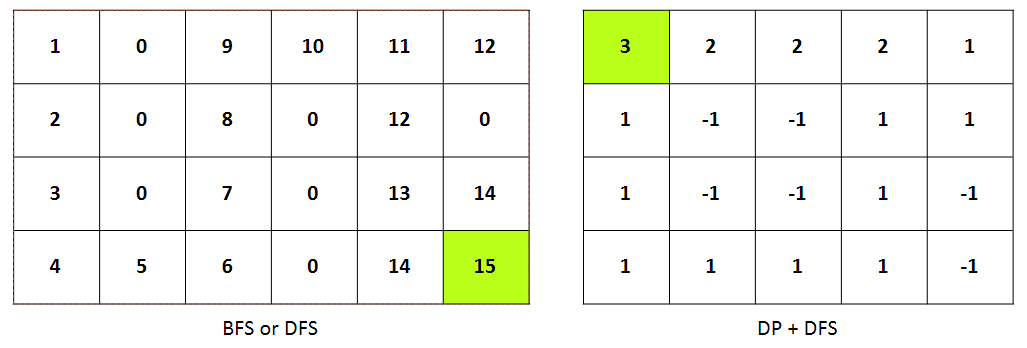
DP + DFS 응용

  • 탐색하려는 그래프의 크기가 클 때 DP와 DFS를 함께 사용
  • 보통 DFS나 BFS를 사용하여 그래프를 탐색할 때 가는 길에 값을 저장하는 경우가 많다.
    이는 이미 지났던 경로를 다시 지나가게 되어서 n이 500이하만 되어도 2초 내에 문제를 풀 수 없다.
  • DP + DFS 방법은 출발점에서 도착점까지 간 후, 돌아오는 길에 값을 저장(계산)하며 온다.
    만약 지났던 길이라면 그 길을 다시 가지 않고, 저장된 값만 가져와서 되돌아간다.

BOJ 2178 vs 1520


누적합

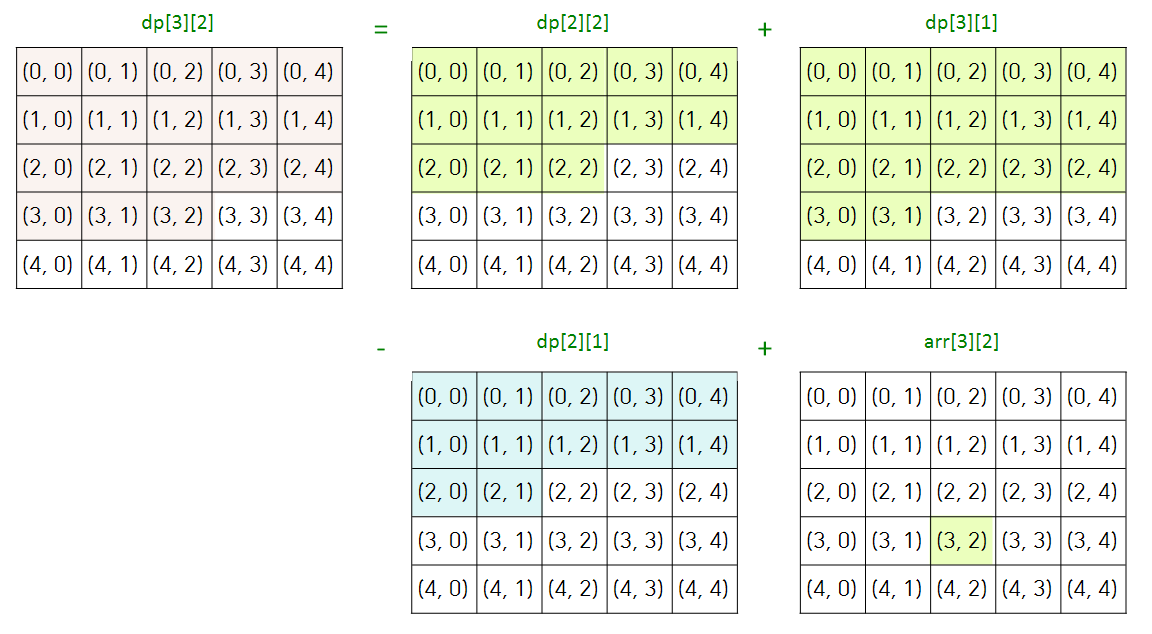
// 1차원
dp[i] = dp[i - 1] + arr[i];

// i ~ j까지의 합
dp[j] - dp[i - 1];

// 2차원
dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + arr[i][j];

// (i1, j1) ~ (i2, j2) 까지의 합
dp[i2][j2] - dp[i1 - 1][j2] - dp[i2][j1 - 1] + dp[i1 - 1][j1 - 1];


Knapsack

  • k 무게까지 들어갈 수 있는 배낭, 가치(value)와 무게(weight)가 있는 n개의 물건이 주어졌을 때 가치의 합이 최대가 될 수 있는 조합을 찾는 것

  • 2차원 배열 dp[i][w] 사용
    - i: 물건 1, 2, 3 ... n
    - w: 배낭 무게 1, 2, 3 ... k

  • i 번째까지의 물건을 무게가 w인 배낭에 넣을 때 최대 가치 저장

for (int i = 1; i < n + 1; i++) {
	for (int j = 1; j < k + 1; j++) {
		if (weight[i] <= j) {
			dp[i][j] = Math.max(dp[i - 1][j], value[i] + dp[i - 1][j - weight[i]]);
		} else {
			dp[i][j] = dp[i - 1][j];
		}
	}
}

진행 순서
1. 물건의 무게 <= 배낭의 무게
   1) 물건을 안 넣는다. (이전에 넣어둔 물건의 가치 유지함)
      OR
   2) 물건을 넣는다. (현재 넣을 물건 가치 +
    ('현재 배낭 무게 - 현재 넣을 물건 무게'에서 얻을 수 있는 최대의 가치))

  1. 물건의 무게 > 배낭의 무게
    1) 물건을 못 넣는다. (이전에 넣어둔 물건의 가치 유지함)

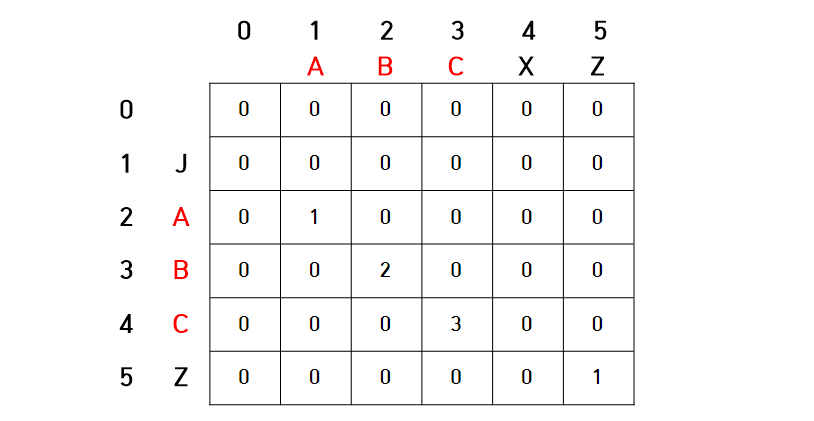
LCS

1) 최장 공통 부분 수열
ex) ABCXZ & JABCZ → ABC

String str1 = br.readLine();
String str2 = br.readLine();
int[][] lcs = new int[str1.length() + 1][str2.length() + 1];

	for (int i = 1; i < str1.length() + 1; i++) {
		for (int j = 1; j < str2.length() + 1; j++) {
			if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
				lcs[i][j] = lcs[i - 1][j - 1] + 1;
				// str1 i-1글자와 str2 j-1글자까지의 공통 부분 수열 길이 + 1
			} else {
				lcs[i][j] = 0;
			}
	}


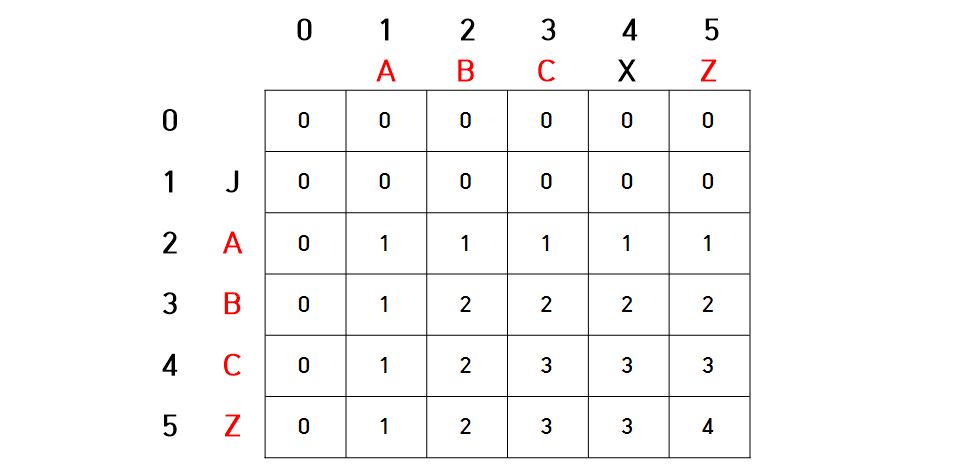
2) 최장 공통 문자열
ex) ABCXZ & JABCZ → ABCZ

String str1 = br.readLine();
String str2 = br.readLine();
int[][] lcs = new int[str1.length() + 1][str2.length() + 1];

	for (int i = 1; i < str1.length() + 1; i++) {
		for (int j = 1; j < str2.length() + 1; j++) {
			if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
				lcs[i][j] = lcs[i - 1][j - 1] + 1;
			} else {
  				// str1 i-1글자까지의 문자열, str2 j-1글자까지의 문자열 중 더 큰 값 가져옴
				lcs[i][j] = Math.max(lcs[i - 1][j], lcs[i][j - 1]);
			}
		}
	}



7. 최단 경로

Dijkstra

  • x 노드에서 출발하여 각 노드로 가는 최단 경로를 구하는 알고리즘
  • 출발점이 정해져 있는지 확인할 것
  • x 노드에서 각 노드까지 갈 수 있는 최단 경로를 업데이트 할 수 있는 배열, Priority Queue 사용
  • distance[] 배열 해석: 현재 시작점에서 [i] 노드로 갈 수 있는 최소 거리는 distance[i]이다.
while (!pQ.isEmpty()) {
	Edge now = pQ.poll();

	if (distance[now.node] < now.weight) {
		continue;
	}

	for (int i = 0; i < graph[now.node].size(); i++) {
		Edge next = graph[now.node].get(i);

		//현재 시작점에서 next 노드로 갈 수 있는 최소 거리가 now를 거쳐 next로 가는 것이 더 빠르다면 업데이트 한다.
		if (distance[next.node] > distance[now.node] + next.weight) {
			distance[next.node] = distance[now.node] + next.weight;
			pQ.offer(new Edge(next.node, distance[next.node]));
		}
	}
}

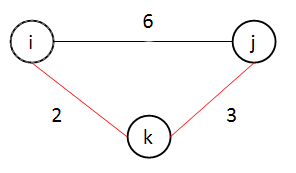
Floyd

  • n 노드에서 n 노드까지의 최단 경로를 모두 구하는 알고리즘
  • 경유지가 존재하는지 확인할 것
  • 한 번에 가는 것보다 경유지 거쳐서 가는 것이 더 빠르면 업데이트 할 것
private static void floyd(int[][] arr) {
	for(int k = 0; k < arr.length; k++) {
		for(int i = 0; i < arr.length; i++) {
			for(int j = 0; j < arr.length; j++) {
				arr[i][j] = Math.min(arr[i][j], arr[i][k] + arr[k][j]);
			}
		}
	}
}



8. 신장 트리

  • 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프

  • 두 노드의 부모가 같다면 같은 집합이라는 뜻


Union & Find

  • 트리를 그래프로 표현하기 위해 필요한 알고리즘

  • find: 부모를 찾는 메서드
private static int find(int[] parent, int x) {
	if (parent[x] != x) {
		parent[x] = find(parent, parent[x]);
	}
	return parent[x];
}
  • union: 같은 집합으로 묶는 메서드
private static void union(int[] parent, int x, int y) {
	int x1 = find(parent, x);
	int y1 = find(parent, y);

	if (x1 < y1) {
		parent[y1] = x1;
	} else {
		parent[x1] = y1;
	}
}

Kruskal

  • 최소 비용으로 만들 수 있는 신장 트리를 찾는 알고리즘
  • weight 정렬할 것, 부모가 같지 않을 때만 weight을 더할 것
private static void kruskal(ArrayList<Edge> graph, int[] parent) {
	Collections.sort(graph, Comparator.comparingInt(o -> o.weight));

	for (Edge edge : graph) {
		if (find(parent, edge.x) != find(parent, edge.y)) {
			union(parent, edge.x, edge.y);
			weight += edge.weight;
		}
	}
}

Topological Sort

  • 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 알고리즘
  • 진입 차수 계산을 위한 degree 배열, Queue 사용
private static void topology(ArrayList<Integer>[] graph, int[] degree) {
	Queue<Integer> queue = new LinkedList<>();
	for (int i = 1; i < degree.length; i++) {
		if (degree[i] == 0) {
			queue.offer(i);
		}
	}

	while (!queue.isEmpty()) {        
		int now = queue.poll();
		for (int i : graph[now]) {
			degree[i]--;
			if (degree[i] == 0) {
				queue.offer(i);
			}
		}               
	}
}


9. 기타

Max, Min

Arrays.stream(arr).max().getAsInt(); 	// arr
Collections.max(list);					// list
Collections.max(map.keySet());			// map-key
Collections.max(map.values());			// map-value


참고

profile
devyumi
이전 포스트

Optional

다음 포스트

Collection vs Collections

0개의 댓글

관련 채용 정보