백준 2493번 탑 & 17298번 오큰수 (Java)

문제

---

해결 과정

---

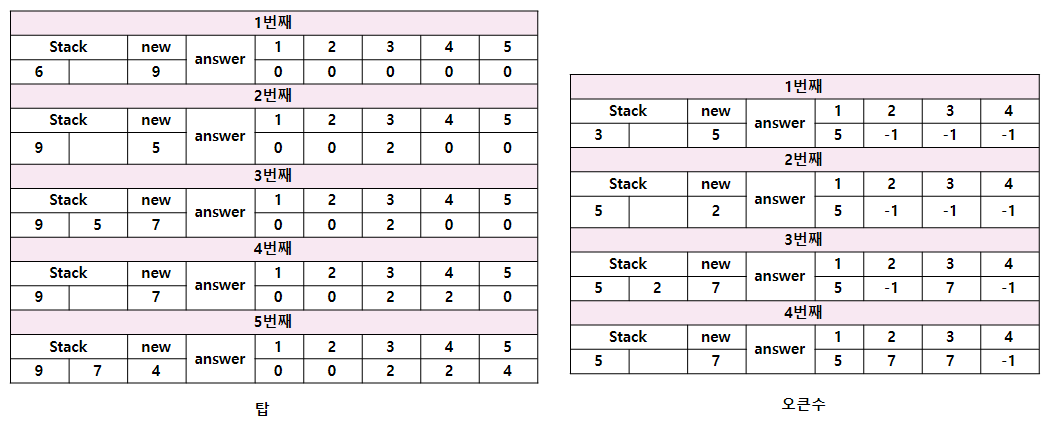
1. Stack

---

두 문제 모두 스택을 사용하여 문제를 해결할 수 있다.

완전 탐색으로 풀 경우 O(n²)으로 시간 초과이기 때문에 O(n)으로 모든 수를 탐색해야 되는 것이 풀이의 핵심이다.

두 문제 모두 Stack 가장 끝 값과 새로운 값의 차이를 비교해서 문제를 풀어야 한다.

오큰수의 경우 새로운 값이 클 때만 조건을 확인해주면 되지만, 탑의 경우 큰 탑을 무조건 찾아야 하기 때문에 반대 조건도 확인해야 한다.

2. 주요 코드

---

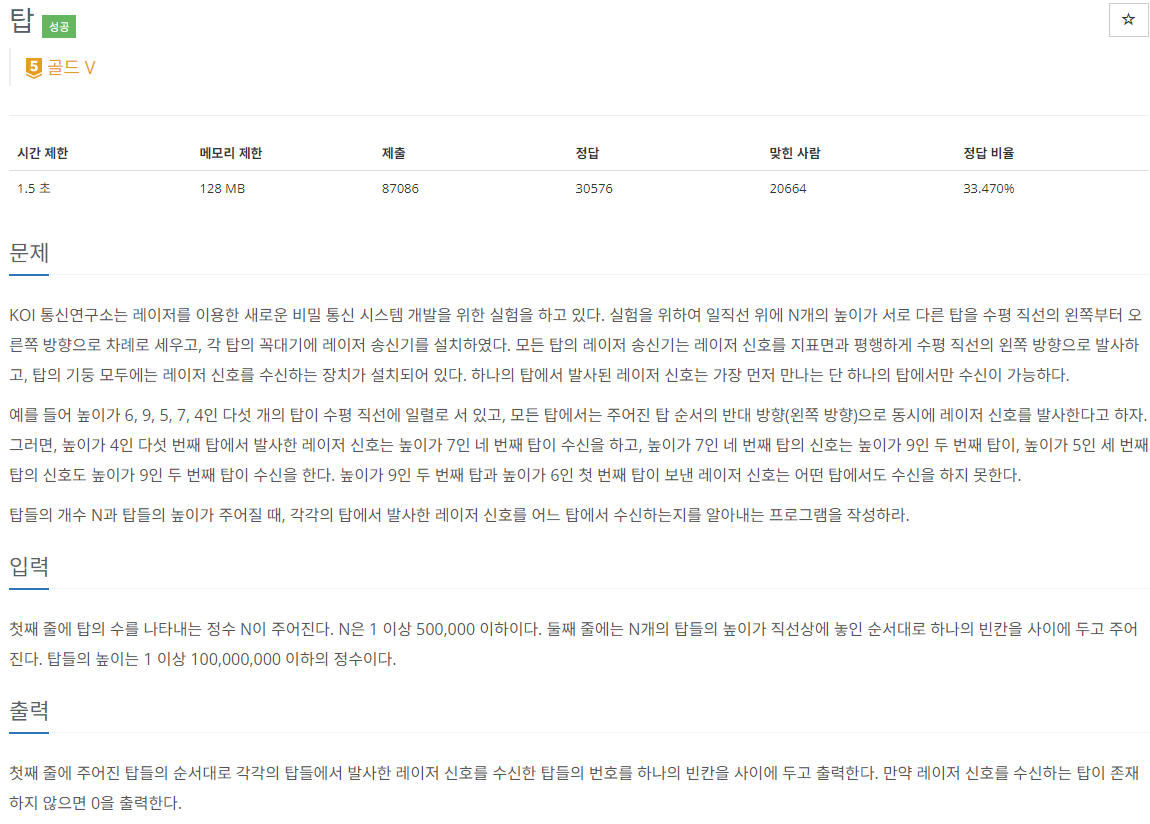
탑

int n = Integer.parseInt(br.readLine());
int[] answer = new int[n];
StringBuilder sb = new StringBuilder();

//{높이, index}
Stack<int[]> stack = new Stack<>();

StringTokenizer st = new StringTokenizer(br.readLine());
stack.push(new int[]{Integer.parseInt(st.nextToken()), 0});

for (int i = 1; i < n; i++) {
	int[] tmp = {Integer.parseInt(st.nextToken()), i};

	if (!stack.isEmpty()) {
		if (stack.peek()[0] > tmp[0]) {
			answer[tmp[1]] = stack.peek()[1] + 1;
		} else {
			while (!stack.isEmpty()) {
				if (stack.peek()[0] > tmp[0]) {
                	//break가 이해되지 않는다면 반례 6 9 5 7 4 8을 생각해볼 것
					answer[tmp[1]] = stack.peek()[1] + 1;
					break;
				} else {
					stack.pop();
				}
			}
		}
	stack.push(tmp);
	}
}

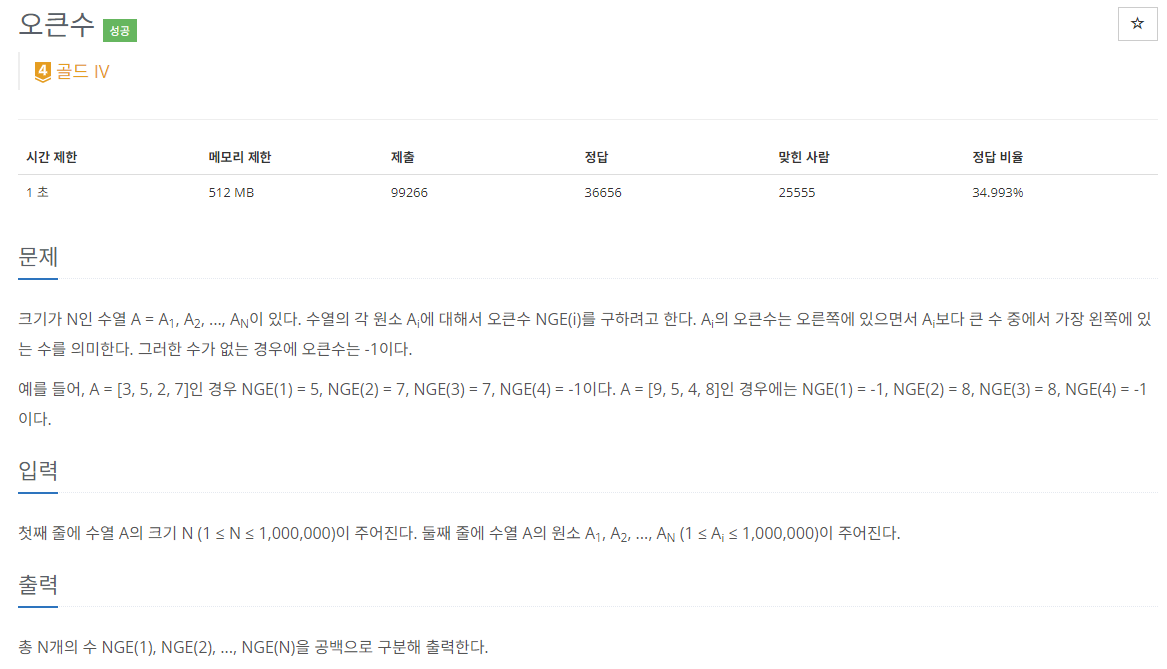
오큰수

int n = Integer.parseInt(br.readLine());
int[] answer = new int[n];
StringBuilder sb = new StringBuilder();
Arrays.fill(answer, -1);

//{수열, index}
Stack<int[]> stack = new Stack<>();

StringTokenizer st = new StringTokenizer(br.readLine());
stack.push(new int[]{Integer.parseInt(st.nextToken()), 0});

for (int i = 1; i < n; i++) {
	int[] num = {Integer.parseInt(st.nextToken()), i};

	while (!stack.isEmpty() && stack.peek()[0] < num[0]) {
		if (answer[stack.peek()[1]] != 1) {
			answer[stack.peek()[1]] = num[0];
			stack.pop();
		}
	}
	stack.push(num);
}