1. phong reflection model 세가지에 대해 설명
ambient reflection
- 빛을 직접 받지 않아도 물체가 보임
- Ia=KaLa
diffuse reflection
- 빛의 입사각에 따라 intensity가 달라짐
- Id=KdLdcosθ=Kd(l⋅n)Ld
specular reflection
- reflection 방향과 일치 시 highlight
- Is=KscosαϕLs=Ks(r⋅v)αLs
2. flat shading, gouraud shading, phong shading 차이점
flat shading
- constant shading
- 점 1개에서 계산 후 polygon 전체를 같은 색으로
- 계산 빨라짐
- 마하 밴드 효과(경계 부분에서 계단 효과)
- vertex 3개 평균해서 점 p 선택
gouraud shading
- interpolation shading
- vertex에 인접한 face마다 face normal vector의 평균
- 각 vertex에서 phong equation 계산
- polygon 내부의 점들은 이중 보간
*주로 길거나 큰 polygon에서 specular reflection의 highlight 부분이 vertex가 아니라 polygon 내부에 위치한 경우 highlight를 놓침
phong shading
- fragment 단위로 색을 계산하여 구로 쉐이딩이 표시 못하는 하이라이트를 표현
- 각 vertex에 대한 법선 벡터들로 bi-linear interpolation을 진행
- 계산량 ↑ but 품질 굿
3. 임의의 점 pivot point 기준 rotation에 대한 변환 행렬 제시하기
rotation
⎣⎢⎢⎢⎡uxvxnx0uyvyny0uzvznz00001⎦⎥⎥⎥⎤
4. model matrix, view matrix, projection matrix를 frame 관련하여 설명
model matrix
- 개별 객체의 위치, 크기, 회전 등을 월드 좌표계로 변환하는 데 사용
view matrix
- 카메라의 위치와 방향을 정의
- 변환된 월드 좌표계에 view matrix를 곱해줌으로써 view 좌표계로 변환 가능
projection matrix
orthogonal projection
- 직육면체 영역을 평행하게 scailing
- 계산 용이
- 길이, 거리 왜곡 X → 설계도
- view frame을 canonical view volume으로 변환
- 필요한 부분만 끊어내기
- qproj=Mprojqview=MprojMviewMmodelqmodel
perspective projection
- 계산 복잡
- 원근감 표현 가능
- 소실점
- ⎣⎢⎢⎢⎡xpypzpwp⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡10000100001d10000⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡xyz1⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡xyz(z/d)⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡(z/d)x(z/d)yd1⎦⎥⎥⎥⎤
- z=d 평면으로 proj 하는 경우
5. VRP, VPN, VUP는 무엇인가. 이들을 world frame 관점에서 view frame으로 전환하기 위한 view matrix 계산을 서술하라
VRP
- view reference point
- 3d point, camera position
VPN
- view plane normal
- view plane에 수직인 벡터
VUP
- view up vector
- view plane의 y방향 설정
view matrix
R⋅⎣⎢⎡100010001⎦⎥⎤=⎣⎢⎡uxuxuxvyvyvynznznz⎦⎥⎤
이고
uview=(1,0,0,0)viewT=Mviewuworld
vview=(0,1,0,0)viewT=Mviewvworld
nview=(0,0,1,0)viewT=Mviewnworld
R−1=RT
이기 때문에
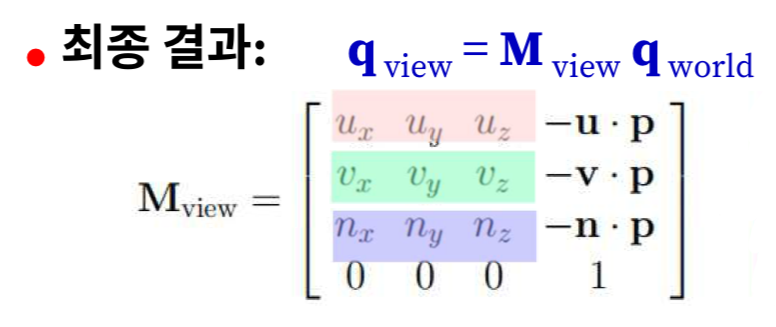
Mview=⎣⎢⎢⎢⎡uxvxnx0uyvyny0uzvznz0???1⎦⎥⎥⎥⎤
이다. 이때
pview=(0,0,0,1)viewT=Mviewpworld
이므로
⎣⎢⎢⎢⎡uxvxnx0uyvyny0uzvznz0???1⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡pxpypz1⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡u⋅p+?v⋅p+?n⋅p+?1⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡0001⎦⎥⎥⎥⎤
6. glsl에서 texture mapping을 사용하기 위한 과정 서술
- vertex shader에서 (s,t) 좌표를 vertex attribute로 설정
- rasterization에서 bi-linear interpolation
- screen space에서 fragment마다 (s,t) 좌표 부여
...
vTexCoord=aTexCoord;
...
- fragment shader에서 texture image 상의 대응되는 (s,t) 위치 가져오기
- 하드웨어로 구현
...
FragColor=texture(texSampler,vTexCoord);
...
texture()
- 주어진 texture image에서 RGBA 컬러 정보 가져오기/계산하기

