출처
https://www.acmicpc.net/problem/15483
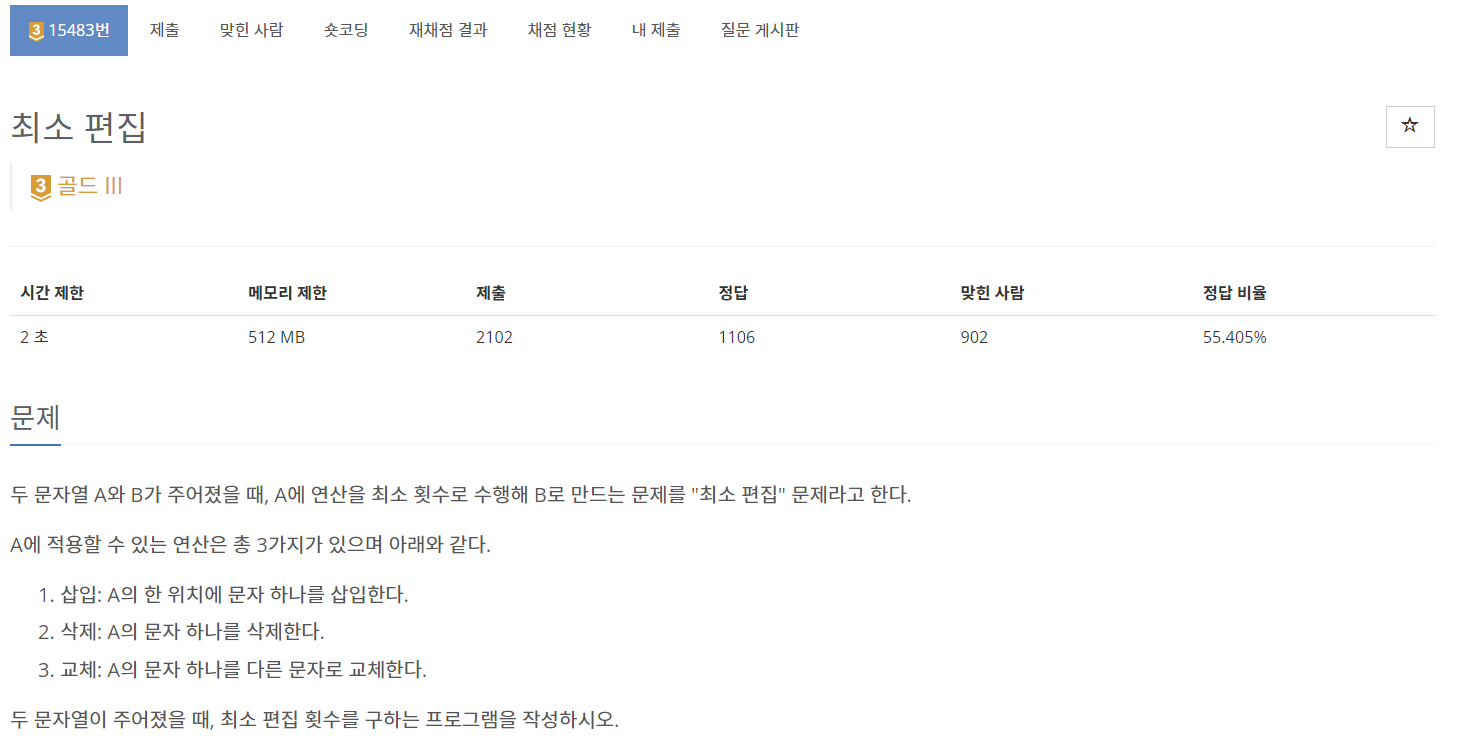
문제
편집 거리 알고리즘을 사용하여 문자열의 유사도를 구하는 문제이다.
편집거리 알고리즘이란?
편집거리 알고리즘은 두 문자열의 유사도를 판단하는 알고리즘이다.
수정, 삽입, 삭제 기능이 있다고 할 때 몇 번의 동작이 필요한지 측정한다. 문자열 내에서 위치 변환 같은 기능이 없다.
2차원 메모이제이션 배열을 사용하는 Dynamic Programming의 한 종류이다.
편집거리 알고리즘의 규칙
- str1에서 i번째 문자와 str2에서 j번째 문자를 서로 비교한다.
- 두 문자가 같으면 dp[i-1][j-1]의 값을 그대로 가져온다.
- 두 문자가 다르면 dp[i-1][j], dp[i][j-1], dp[i-1][j-1] 중 최소값에 1을 더해서 dp[i][j]에 저장

편집 거리는 다음과 같이 표를 이용해 구한다.
문자열의 부분 문자열을 구해 부분 문자열끼리 비교한 편집 거리를 표에 작성한다.
이 때, 아직 채워지지 못한 바로 오른쪽이나 아래쪽, 대각선으로 우측 하단 방향에 대해서는 마지막 문자만을 비교해 추가 혹은 변경이 발생했는지 확인하면 된다.
추가 혹은 변경이 발생해야 한다면 1을 더하고, 아니라면 이전 값과 동일한 값을 넣는다.
위 과정은 적절한 점화식으로 표현할 수 있다.
마지막 문자가 같으면, 점화식은 다음과 같다. 최소 편집 거리는 대각선 인접 칸과 같다.
마지막 문자가 서로 다르면, 편집이 1회 일어나 근처 3칸 중 최솟값에서 1을 더한 값이다.
즉 다음과 같은 점화식을 활용해 동적 계획법으로 최소 편집 거리를 빠르게 구할 수 있다.
예를 들자면,
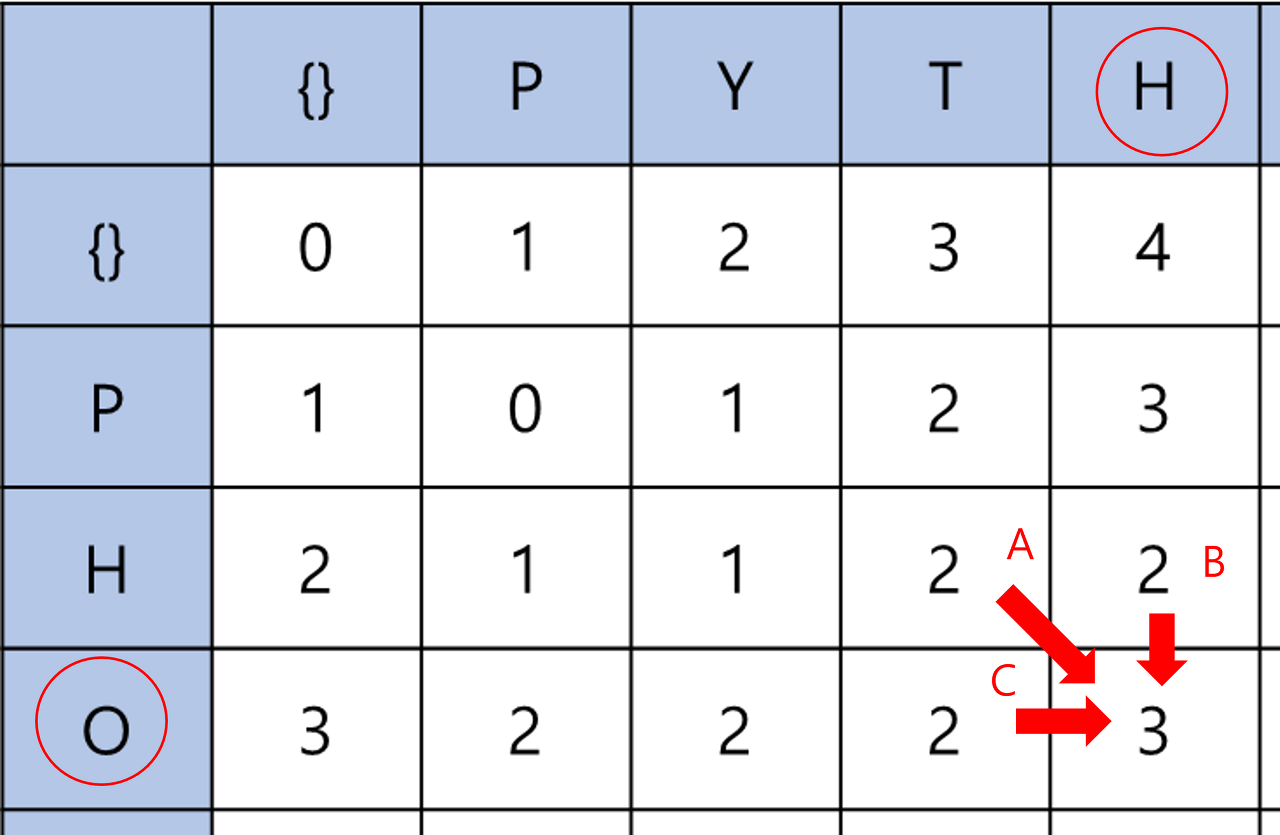
'O'와 'H'를 비교한 경우를 생각해보자.
- A의 경우를 보면 'PH'에서 'PYT'로 2번의 연산으로 변환이 되었다고 생각한다. 다음 줄로 오면서 'O'가 더해지고 'PYTO'가 된 상황이다. 이 때는 'O'를 'H'로 수정 연산을 하면 된다.
- B의 경우 'PH'를 'PYTH'로 2번의 연산으로 변환이 되었다고 생각한다. 마찬가지로 다음 줄로 넘어가면서 'O'가 더해지고 'PYTHO'가 된 상황이다. 이 경우에는 'O'를 삭제 연산을 하게 되면 'PYTH'로 만들 수 있다.
- C의 경우 'PHO'를 'PYT'로 2번의 연산으로 변환이 되었다고 생각한다. 이 경우에는 다음 줄이 되는 것이 아니므로 'O'가 더해지는 것은 아니다. 'PYT'에서 'H'를 삽입하는 연산을 하게 되면 'PYTH'로 만들 수 있다.
각각의 횟수는 2번의 연산에 한 번 더 연산을 하는 과정이 필요하므로 3번 연산을 하면 'PHO'를 'PYTH'로 바꿀 수 있다. 우리는 최소 편집 거리를 찾기 때문에 A, B, C 과정을 한 후 최소값을 dp 테이블에 넣어주면 된다.
위에서 같은 문자끼리 비교하는 경우에는 A의 연산의 특수한 경우로 생각하면 된다. 수정 연산을 생각할 때 두 문자가 같으므로 수정을 굳이 안 해도 되는 경우라고 생각한다. 그리고 dp[i-1][j-1]은 dp[i-1][j] + 1, dp[i][j-1] + 1과 비교했을 때 최솟값을 가지는 것이 보장된다.
코드
n = input()
ans = input()
dp = [[0 for _ in range(len(ans)+1)] for _ in range(len(n)+1)]
for i in range(len(n)+1):
dp[i][0] = i
for i in range(len(ans)+1):
dp[0][i] = i
for i in range(1, len(n)+1):
for j in range(1, len(ans)+1):
if n[i-1] == ans[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 1, dp[i-1][j] + 1, dp[i][j-1] + 1)
print(dp[-1][-1])
참고자료 및 출처
https://joyjangs.tistory.com/38
코테 스터디 Notion
