[Algorithm] 0x0B 재귀

출처: https://blog.encrypted.gg/943?category=773649
본 게시글은 개인 공부를 위해 위 링크를 토대로 요약한 글입니다.

💡 알고리즘 설명

1️⃣ 재귀

하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘

void nums(int n) {
	if (n == 0) return;
	nums(n - 1);
	cout << n << ' ';
}
// n이 5일 때, 출력 -> 1, 2, 3, 4, 5

int factorial(int n) {
	if (n == 0) return 1;
	return n * factorial(n - 1);
}
// n이 3일 때, 최종 반환 값 -> 6 (1 * 1 * 2 * 3)

위 예시 코드는 알고리즘을 풀어봤다면, 한 번쯤은 볼 수 있는 재귀 함수라고 생각되는데,
위 함수가 어떻게 올바른 결과를 보여주는 걸까?

2️⃣ 수학적 귀납법

수학적 귀납법을 쉽게 이야기 해보면,
k일에 피부 깨끗, k + 1일에 피부 깨끗이 참이면,
피부가 오늘도 깨끗하고 내일도 깨끗하면 평생 깨끗하다. 라는 결론이 나온다.

우리가 재귀로 문제를 푼다는 것은 귀납적인 방식으로 문제를 해결한다는 것인데,
이 귀납적인 방식이란 것은 우리의 상식과 큰 차이가 있다.
이를 제대로 이해하고 있어야 재귀를 통해 문제를 푸는 과정에서 헤매지 않는다.

도미노를 예시를 보면, 도미노에서 제일 앞 도미노를 쓰러뜨리면 모든 도미노가 쓰러진다.
이 예시에서 왜 모든 도미노가 쓰러지는 지 설명하라 한다면 두 가지 방식이 있다.

첫 번째로는 ‘1번 도미노가 쓰러지면 2번 도미노가 쓰러지고, 2번 도미노가 쓰러지면 3번 도미노가 쓰러지고...’ 이런 식으로 반복하면 모든 도미노가 쓰러진다. 라고 설명할 수 있다.

두 번째로는 ‘1번 도미노가 쓰러진다.’ ‘k번 도미노가 쓰러지면, k + 1번 도미노가 쓰러진다.’가 참이면 모든 도미노가 쓰러진다는 설명 방법이다.

두 번째 방식도 결국 1번 도미노가 쓰러지고, 2번 도미노가 쓰러져서 진행되는 방식이지만, 재귀를 사용하기 위해서는 이러한 절차지향적 사고를 탈피해야 한다.

• 절차지향적 사고

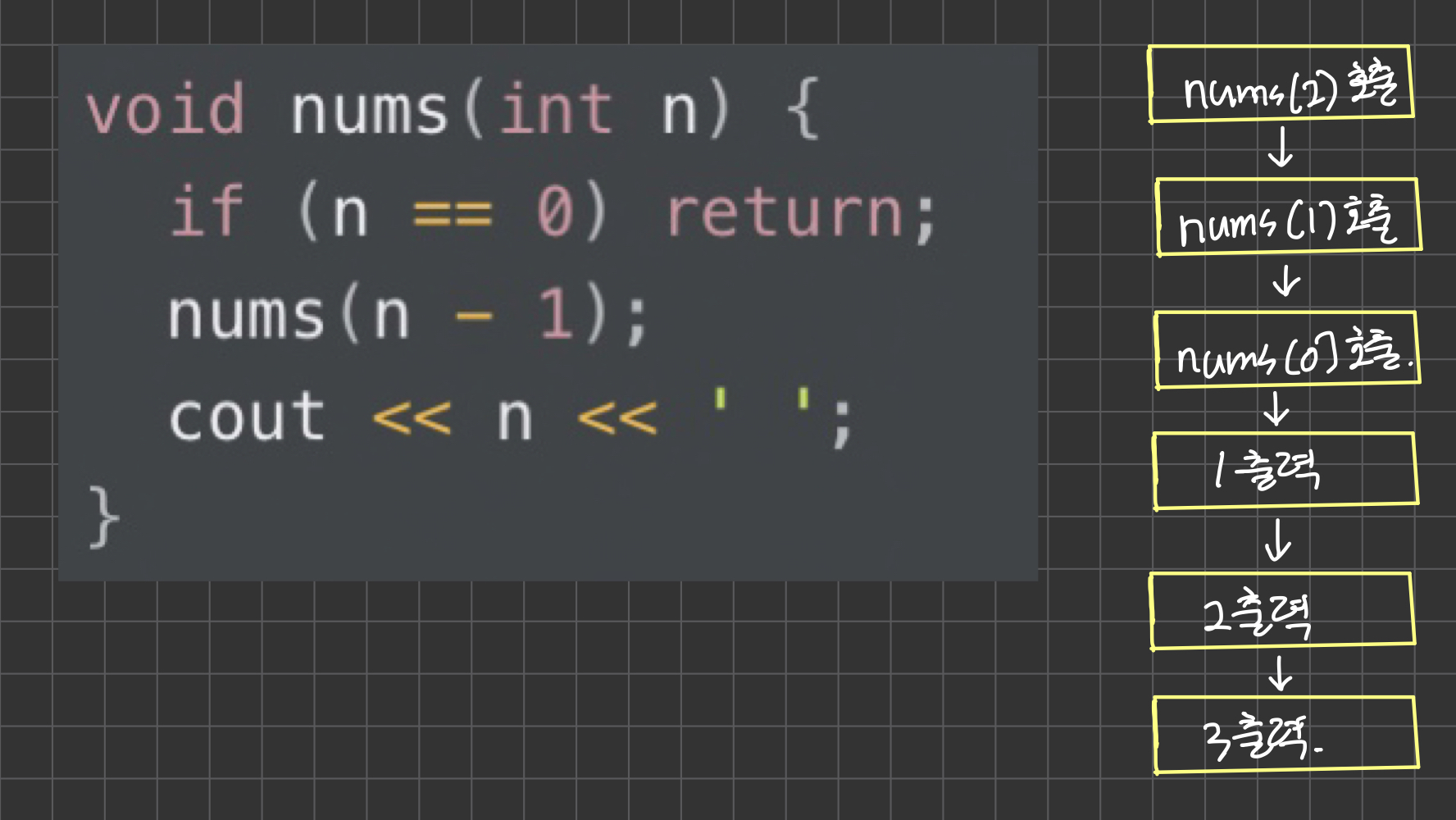
  절차지향적 사고는, 위 코드가 동작하는 흐름을 그대로 따라간다.

• 귀납적 사고

  귀납적 사고는 ‘nums(1)이 1을 출력한다.’ 라는 사실과
  ‘nums(k)가 1...k-2 k-1 k 까지 출력하는 것과,
  nums(k+1)이 1...k-1 k k+1 까지 출력한다.’는 사실로
  nums 함수가 1부터 n까지 출력하는 함수임을 알 수 있다.

위 내용을 살펴보고 재귀 함수가 올바른 결과를 낼 때, 과정을 하나하나 따라가는 것보다 귀납적 사고로 이해해보길 바란다.

3️⃣ 재귀 함수의 조건

• 특정 입력에 대해서는 자기 자신을 호출하지 않고 종료되어야 한다.(Base condition) 귀납적 사고 예시 코드에서 n == 0 일 때, 자기 자신을 호출하지 않고 종료한다.
  

• 모든 입력은 base condition으로 수렴해야 한다. 우리는 위 함수에 자연수만 넣게 되니 모든 입력은 최종적으로 n = 0 으로 수렴한다.
  

위 두 조건 중 하나라도 지키지 않으면 재귀 함수는 결과를 내지 않고 무한히 돌아간다.

4️⃣ 재귀에 대한 정보

• 함수의 인자로 어떤 것을 받아서 어디까지 계산하고 자기 자신에게 넘겨줄 지 명확히 해야한다.

• 모든 재귀 함수는 반복문만으로 동일한 동작을 하는 함수를 만들 수 있다.

• 재귀는 반복문으로 구현 했을 때에 비해 코드가 간결하지만, 메모리/시간에서 비용이 크다.

• 한 함수가 자기 자신을 여러 번 호출하게 되면 비효율적일 수 있다.
  (예시로 피보나치를 재귀만 사용하여 구현 시 O(1.618 ^ n) 시간 복잡도를 가진다.)

• 재귀 함수가 자기 자신을 부를 때, 스택 영역에 계속 누적된다.
  (스택 메모리를 과도하게 사용할 위험이 있다.)

✏️ 연습 문제(BOJ)

문제 분류	문제	문제 제목
연습 문제	1629	곱셈
연습 문제	11729	하노이 탑 이동 순서
연습 문제	1074	Z
기본 문제✔	17478	재귀함수가 뭔가요?
기본 문제✔	1780	종이의 개수
기본 문제✔	2630	색종이 만들기
기본 문제✔	1992	쿼드트리
응용 문제✔	2447	별 찍기 - 10
응용 문제✔	2448	별 찍기 - 11
응용 문제	14956	Philosopher’s Walk