
트리(Tree)?
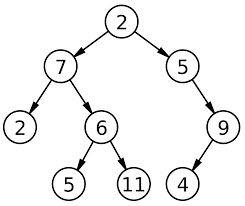
각 정점 : 노드라고 부름
루트 노드 : 가장 상위에 존재하는 노드
레벨 : 루트로 부터 몇 번째 깊이인지 사용 (루트 노드 = 레벨 1)
차수 : 정점으로 부터 뻗어나가는 간선의 수
트리는 방향 그래프의 일종으로 정점을 가리키는 간선이 하나 밖에 없는 구조를 가지고 있다.
트리는 그래프와 다르게 사이클이 발생하지 않는다.
트리 구현은 인접 행렬과 인접 리스트 방법 2가지가 있다.
트리 특징
- 루트 정점을 제외한 모든 정점은 반드시 하나의 부모 정점을 가진다.
- 정점이 N개인 트리는 반드시 N-1개의 간선을 가진다.
- 루트에서 특정 점으로 가는 경로는 유일하다.
일반 트리의 구현
일반 트리의 구현은 그래프와 동일하게 구현하면 된다.
- 인접 행렬
const matrix = [
[0, 5, 3],
[0, 0, 0],
[0, 0, 0],
]- 인접 리스트
const graph = {
1 : [ {arrive : 5, cost : 10}, {arrive : 3, cost : 8} ],
3 : [ {arrive : 1, cost : 8} ],
5 : [ {arrive : 1, cost : 10 }, ],
}이진 트리(Binary Tree)?
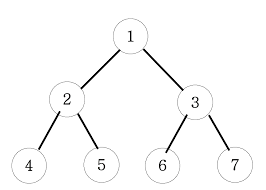
이진 트리는 일반 트리 구조에서 각 정점이 최대 2개의 자식을 가지는 트리다.
이진 트리 종류
- 완전 이진 트리 : 마지막 레벨을 제외하고 모든 정점이 채워져있는 트리
- 포화 이진 트리 : 마지막 레벨로 포함하고 모든 정점이 채워져있는 트리
- 편향 트리 : 한 방향으로만 이어지는 트리
이진 트리 특징
- 정점이 N개인 이진 트리는 최악의 경우 높이가 N이 될 수 있다. ( 편향 트리 )
- 정점이 N개인 포화 또는 완전 이진 트리의 높이는 O(logn)이다.
- 높이가 h인 포화 이진 트리는 2^h - 1의 정점을 가진다.
- 일반적인 이진 트리를 사용하는 경우는 많지 않고 이진 탐색트리, 힙, AVL트리, 레드 블랙 트리에서 응용된다.
이진 트리는 배열과, 연결 리스트 두 가지 방법으로 구현이 가능하다.
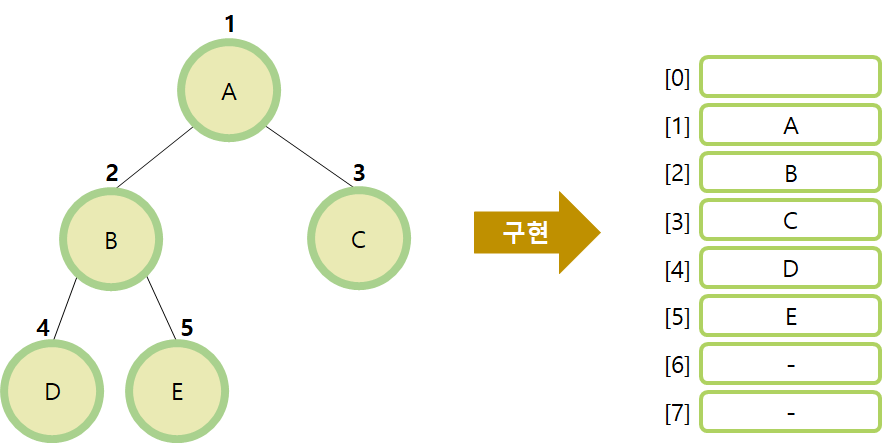
배열로 구현
부모 노드 : Math.floor(index / 2)
왼쪽 자식 노드 : index x 2
오른쪽 자식 노드 : 인덱스 x 2 + 1
class BinaryTree {
constructor() {
this.array = [null];
}
insert(value) {
this.array.push(value);
}
getLeftChild(index) {
return this.array[2 * index];
}
getRightChild(index) {
return this.array[2 * index + 1];
}
getParent(index) {
return Math.floor(index / 2);
}
}
const tree = new BinaryTree();
tree.insert(9); // root
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
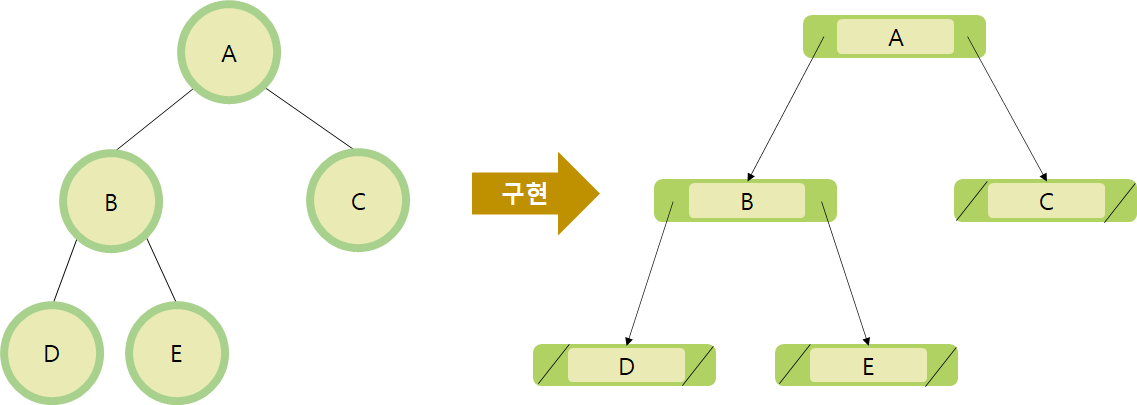
console.log(tree.array); // [null,9,5,4,7,8,5,6]연결 리스트로 구현
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinaryTree {
constructor(node) {
this.root = node;
}
display() {
const queue = [];
queue.push(this.root);
while(queue.length > 0) {
const currentNode = queue.shift();
console.log(currentNode.value);
if(currentNode.left) {
queue.push(currentNode.left);
}
if(currentNode.right) {
queue.push(currentNode.push(currentNode.right));sc
}
}
}
}
const tree = new Tree(new Node(9));
tree.root.left = new Node(3);
tree.root.right = new Node(8);
tree.root.left.left = new Node(2);
tree.root.left.right = new Node(5);이진 트리의 순회
이진 트리의 모든 값을 순회하면서 확인하고 싶을 때 알고리즘의 종류가 있다. 어떤 순서로 순회를 하는가에 따라 전위순회, 중위순회, 후위 순회로 나뉜다.
- 전위 순회 (Pre-Order Traversal)
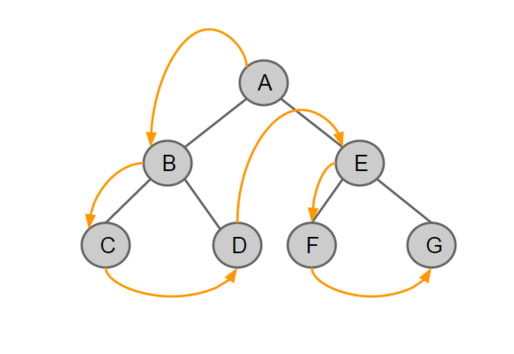
루트 -> 왼쪽 서브트리 -> 오른쪽 서브트리의 순서로 노드를 방문한다.
현재 노드를 처리하고, 그 다음에 왼쪽 자식과 오른쪽 자식을 차례대로 방문한다.
- 중위 순회 (In-Order Traversal)
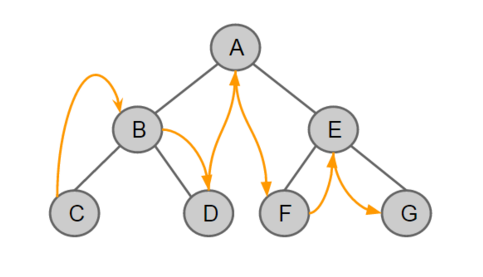
왼쪽 서브트리 -> 루트 -> 오른쪽 서브트리의 순서로 노드를 방문한다.
왼쪽 자식을 가장 우선적으로 방문하고, 그 다음에 현재 노드를 처리한 후 마지막으로 오른쪽 자식을 방문한다.
- 후위 순회 (Post-Order Traversal)
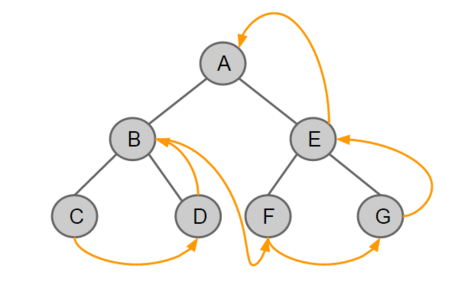
왼쪽 서브트리 -> 오른쪽 서브트리 -> 루트의 순서로 노드를 방문한다.
왼쪽과 오른쪽 자식들을 모두 처리한 후 마지막으로 현재노드를 처리한다.
class BinaryTree {
constructor() {
this.array = [null];
}
getLeftChildIndex(index) {
return index * 2;
}
getRightChildIndex(index) {
return (index * 2) + 1;
}
getParentIndex(index) {
return Math.floor(index / 2);
}
insert(value) {
if(!value) {
return;
}
this.array.push(value);
}
/* 전위 순회 */
preorderTraverse(currentIndex = 1) {
const leftChildIndex = this.getLeftChildIndex(currentIndex);
const rightChildIndex = this.getRightChildIndex(currentIndex);
let result = `${this.array[currentIndex]} -> `;
// 왼쪽 마지막 노드까지 이동
if(leftChildIndex < this.array.length) {
result += this.preorderTraverse(leftChildIndex);
}
// 왼쪽 노드 방문이 끝나면 오른쪽 노드 방문
if(rightChildIndex < this.array.length) {
result += this.preorderTraverse(rightChildIndex);
}
return currentIndex === 1 ? result.slice(0, -4) : result;
}
/* 중위 순회 */
inorderTraverse(currentIndex = 1) {
const leftChildIndex = this.getLeftChildIndex(currentIndex);
const rightChildIndex = this.getRightChildIndex(currentIndex);
let result = "";
// 왼쪽 마지막 노드까지 이동
if(leftChildIndex < this.array.length) {
result += this.inorderTraverse(leftChildIndex);
}
result += `${this.array[currentIndex]} -> `;
// 왼쪽 노드 방문이 끝나면 오른쪽 노드 방문
if(rightChildIndex < this.array.length) {
result += this.inorderTraverse(rightChildIndex);
}
return currentIndex === 1 ? result.slice(0, -4) : result;
}
/* 후위 순회 */
postorderTraverse(currentIndex = 1) {
const leftChildIndex = this.getLeftChildIndex(currentIndex);
const rightChildIndex = this.getRightChildIndex(currentIndex);
let result = "";
// 왼쪽 마지막 노드까지 이동
if(leftChildIndex < this.array.length) {
result += this.postorderTraverse(leftChildIndex);
}
// 왼쪽 노드 방문이 끝나면 오른쪽 노드 방문
if(rightChildIndex < this.array.length) {
result += this.postorderTraverse(rightChildIndex);
}
result += `${this.array[currentIndex]} -> `;
return currentIndex === 1 ? result.slice(0, -4) : result;
}
}
const tree = new BinaryTree();
tree.insert(9); // root 노드
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
console.log(tree.array);
console.log("preorder result : ", tree.preorderTraverse(1));
console.log("inorder result : ", tree.inorderTraverse(1));
console.log("postorder result : ", tree.postorderTraverse(1));