
이진 탐색(Binary Search)?
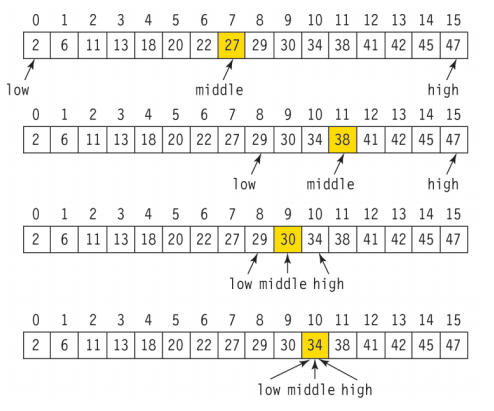
이진 탐색은 정렬 되어있는 요소들을 반씩 제외하며 찾는 알고리즘이며 O(logN)의 시간복잡도가 걸린다.
이진 탐색 특징
- 반드시 정렬이 되어야 사용할 수 있다.
- 배열 혹은 이진 트리를 이용하여 구현할 수 있다.
- O(logN)의 시간복잡도인 만큼 굉장히 빠르다.
배열로 구현
배열로 구현하게 되면 추가와 삭제시 선형 시간 O(n)만큼 걸리는 단점이 있다.
const array = [1, 1, 5, 124, 400, 599, 1004, 2876, 8612];
function binarySerach(array, findValue) {
let left = 0;
let right = array.length - 1;
let mid = Math.floor((left + right) / 2);
while(left < right) {
if(array[mid] === findValue) {
return mid;
}
if(array[mid] < findValue) {
left = mid + 1;
}
else {
right = mid - 1;
}
mid = Math.floor((left + right) / 2);
}
return -1;
}
console.log(binarySerach(array, 2876));
console.log(binarySerach(array, 1));
console.log(binarySerach(array, 500));이진 탐색 트리로 구현
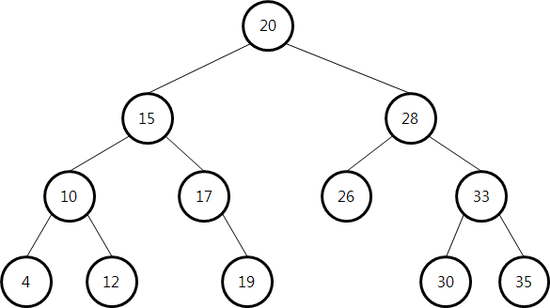
이진 탐색을 위한 이진 트리로 왼쪽 서브 트리는 루트보다 작은 값이 모여있고 오른쪽 서브 트리는 루트보다 큰 값이 모여있다.
이진 탐색 트리 문제점
- 최악의 경우 한쪽으로 편향된 트리가 될 수 있다.
- 그런 경우 순차 탐색과 동일한 시간 복잡도를 가진다.
- 이를 해결하기 위해 AVL 트리, 레드-블랙 트리를 사용할 수 있다.
class Node {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class BinarySearchTree {
constructor(node) {
this.root = node;
}
insert(value) {
const newNode = new Node(value);
// 루트노드가 생성되지 않았으면 루트 노드로 지정
if(this.root === null) {
return this.root = newNode;
}
let currentNode = this.root;
// 루트를 기준으로 크면 오른쪽 작으면 왼쪽으로 루트를 변경하면서 자기 자리를 찾아간다.
while(currentNode !== null) {
// 현재 루트 노드보다 크면
if(currentNode.value < value) {
// right에 아무런 노드가 없다면 right를 가르키고 종료
if(currentNode.right === null) {
currentNode.right = newNode;
break;
}
// right에 노드가 더 있다면 그 노드를 루트로 재 탐색
currentNode = currentNode.right;
}
// 현재 루트 노드보다 작으면
else {
// left에 아무런 노드가 없으면 left를 가르키고 종료
if(currentNode.left === null) {
currentNode.left = newNode;
break;
}
// left에 노드가 더 있다면 그 노드를 루트로 재 탐색
currentNode = currentNode.left;
}
}
}
has(value) {
let currentNode = this.root;
// 현재 노드가 null이 아닐때 까지 반복해서 찾는다.
while(currentNode !== null) {
// 현재 노드의 value가 찾고자 하는 값이면 true 반환
if(currentNode.value === value) {
return true;
}
// 찾는 값이 없고 찾고자 하는 값이 현재 노드의 값보다 크면 오른쪽으로 노드를 이동
if(currentNode.value < value) {
currentNode = currentNode.right;
}
// 찾는 값이 없고 찾고자 하는 값이 현재 노드의 값보다 작으면 왼쪽으로 노드를 이동
else {
currentNode = currentNode.left;
}
}
// 더이상 탐색할 노드가 없으면 false를 반환
return false;
}
delete(value) {
let currentNode = this.root;
let parentNode = null;
while(currentNode !== null) {
// 현재 노드의 value가 찾고자 하는 값이면 해당 노드에서 멈춘다.
if(currentNode.value === value) {
break;
}
// 찾는 값이 없고 찾고자 하는 값이 현재 노드의 값보다 크면 오른쪽으로 노드를 이동
if(currentNode.value < value) {
parentNode = currentNode;
currentNode = currentNode.right;
}
// 찾는 값이 없고 찾고자 하는 값이 현재 노드의 값보다 작으면 왼쪽으로 노드를 이동
else {
parentNode = currentNode;
currentNode = currentNode.left;
}
}
// 삭제할 노드를 찾지 못했다면 종료
if(currentNode === null) {
return;
}
// 자식이 없는 경우
if(!currentNode.left && !currentNode.right) {
// 삭제할 노드가 부모의 왼쪽에 있는 경우
if(parentNode.value > currentNode.value) {
parentNode.left = null;
}
// 삭제할 노드가 부모의 오른쪽에 있는 경우
else {
parentNode.right = null;
}
}
// 자식이 왼쪽 1개 경우
else if(currentNode.left && !currentNode.right) {
// 삭제할 노드가 부모의 왼쪽에 있는 경우
if(parentNode.value > currentNode.value) {
parentNode.left = currentNode.left;
}
// 삭제할 노드가 부모의 오른쪽에 있는 경우
else {
parentNode.right = currentNode.left;
}
}
// 자식이 오른쪽 1개 경우
else if(!currentNode.left && currentNode.right) {
// 삭제할 노드가 부모의 왼쪽에 있는 경우
if(parentNode.value > currentNode.value) {
parentNode.left = currentNode.right;
}
// 삭제할 노드가 부모의 오른쪽에 있는 경우
else {
parentNode.right = currentNode.right;
}
}
// 자식이 2개 경우
else if(currentNode.left && currentNode.right) {
// 삭제할 노드가 부모의 왼쪽에 있는 경우
if(parentNode.value > currentNode.value) {
let target = currentNode.right;
let targetParent = currentNode.right;
// target과 targetParent를 찾음.
while (target.left) {
targetParent = target;
target = target.left;
}
// current의 오른쪽으로 넘어와서 target에 left가 없을 경우 targetParent와 target가 같아짐
if (targetParent === target) {
parentNode.left = target;
target.left = currentNode.left;
currentNode.right = null;
}
else {
// target에 left가 있는 경우
if (target.right) {
// target의 오른쪽이 있으면
targetParent.left = target.right;
} else {
// target의 오른쪽이 없으면
targetParent.left = null;
}
parentNode.left = target;
target.right = currentNode.right;
target.left = currentNode.left;
}
}
else {
// 삭제할 노드가 부모의 오른쪽에 있는 경우
let target = currentNode.right;
let targetParent = currentNode.right;
// target과 targetParent를 찾음.
while (target.left) {
targetParent = target;
target = target.left;
}
// current의 오른쪽으로 넘어와서 target에 left가 없을 경우 targetParent와 target가 같아짐
if (targetParent === target) {
parentNode.right = target;
target.left = currentNode.left;
currentNode.right = null;
}
else {
if (target.right) {
// target의 오른쪽이 있으면
targetParent.left = target.right;
}
else {
// target의 오른쪽이 없으면
targetParent.left = null;
}
parentNode.right = target;
target.right = currentNode.right;
target.left = currentNode.left;
}
}
}
}
}
const tree = new BinarySearchTree(new Node(9));
tree.insert(5);
tree.insert(4);
tree.insert(7);
tree.insert(8);
tree.insert(5);
tree.insert(6);
tree.insert(2);
tree.delete(8);
console.log(tree.has(8)); // false;
console.log(tree.has(1)); // false;