[백준 BOJ] - 최소 스패닝 트리 1197 Java

문제링크: https://www.acmicpc.net/problem/1197

문제설명

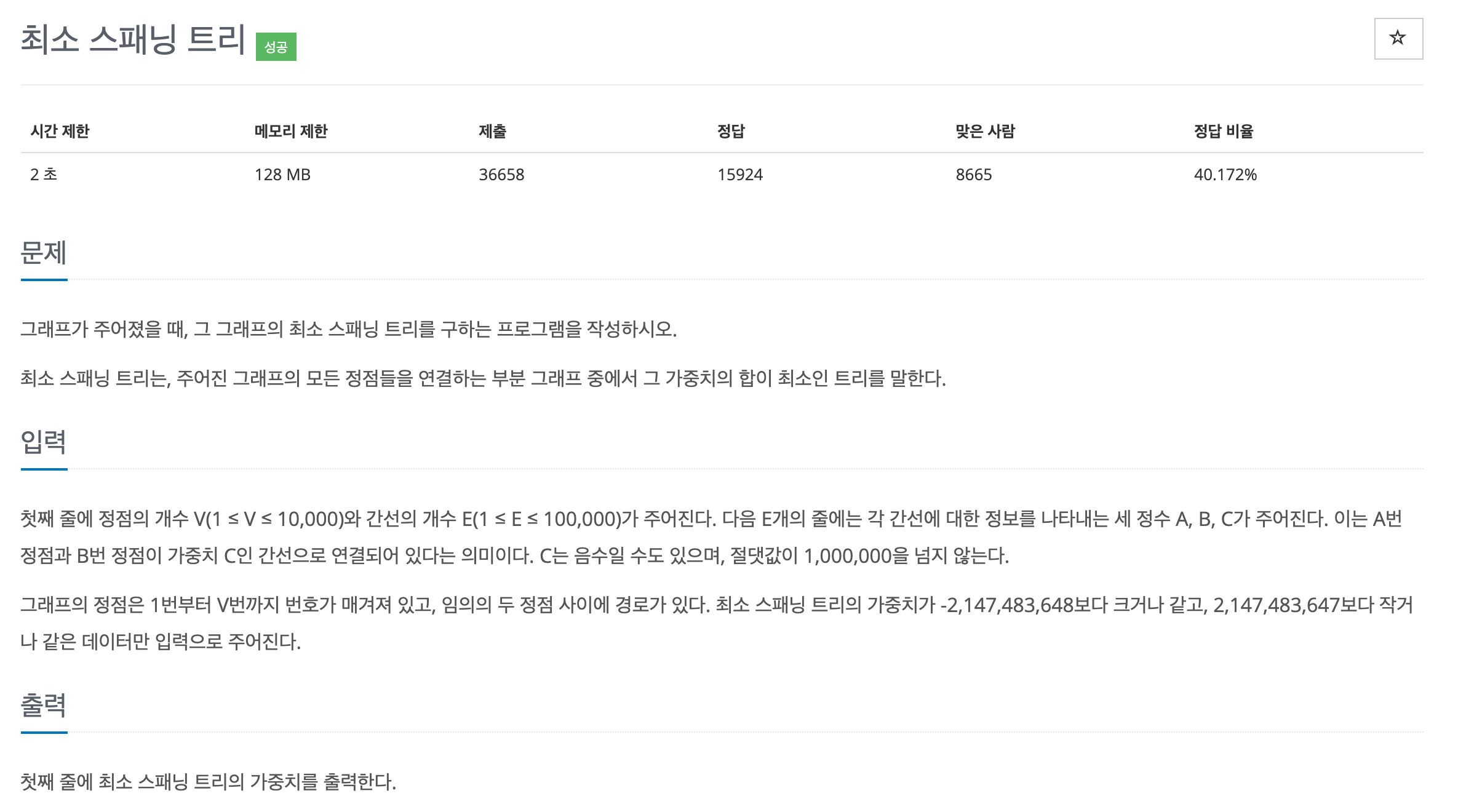
입출력

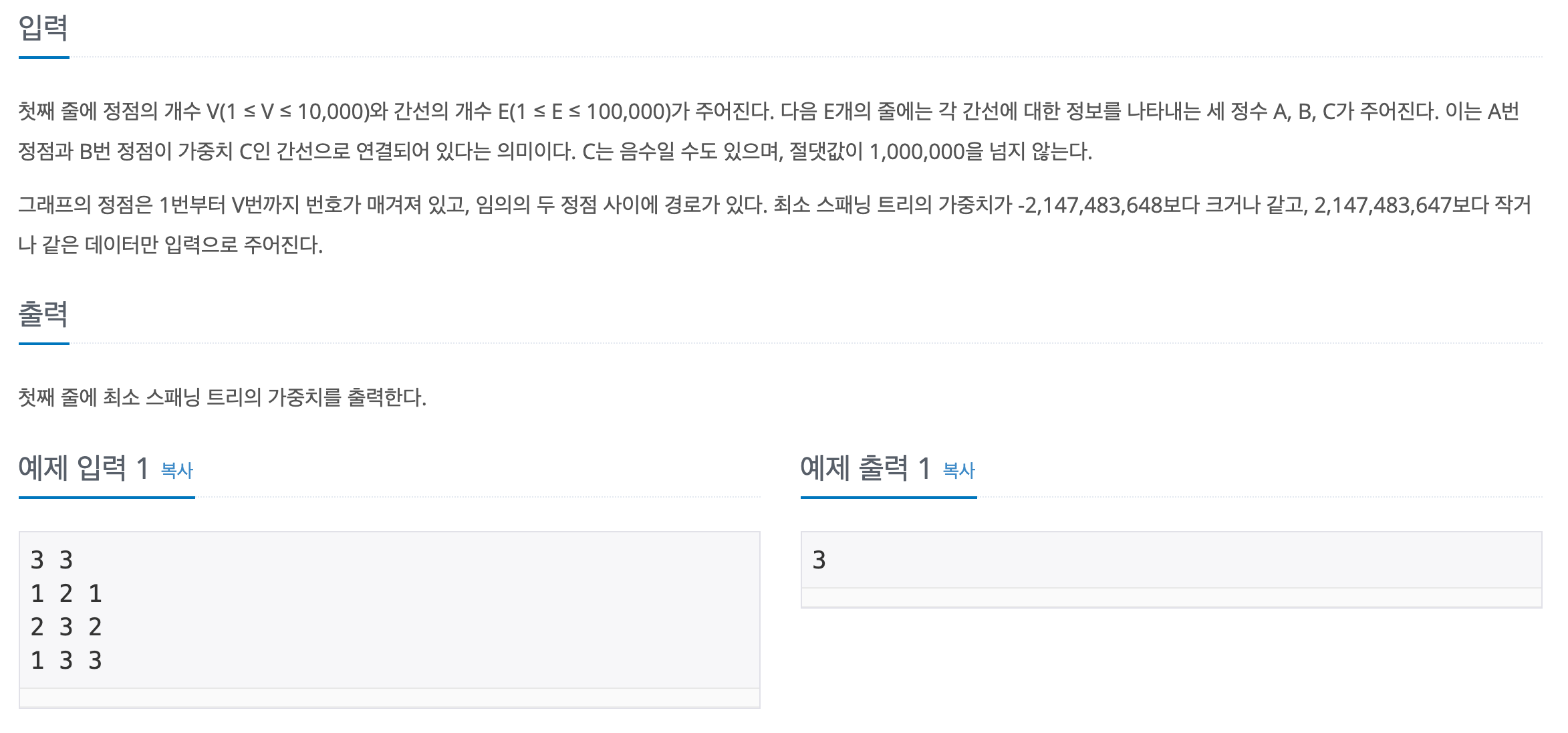
최소 스패닝 트리

최소 스패닝 트리(최소신장트리)는 모든 정점을 지나는 간선의 가중치를 최소로 하는 트리입니다.

n개 정점이 있다면 n-1개 간선만으로 모든 정점을 지나는 그래프를 구성해야 합니다.

최소 스패닝 트리는 크루스칼 알고리즘을 이용합니다.
크루스칼 알고리즘은 최소 스패닝 트리를 구하는데 아주 좋은 아이디어를 제공합니다.

크루스칼 알고리즘

• 가중치를 최소로 👉🏻 가중치를 기준으로 오름차순 정렬
• 사이클(순환)이 발생한다면 그래프에 포함시키지 않는다.
• 사이클이 발생하지 않는다면 그래프에 포함시킨다.
• 즉, 사이클이 발생하지 않는 간선을 가중치가 작은 순서대로 그래프에 포함시키는 것.

선행 알고리즘
Union-Find

• 부모노드를 찾음 (Find)
• 사이클 발생 여부 (Find)
• 부모노드가 서로 다르다면 합쳐줌 (Union)

Union-Find 알고리즘을 이용해서 위 3가지를 기능을 구현할 수 있습니다.

Union-Find에 대해서 너무 좋은 설명이 있어서 설명은 아래 링크로 대체할께요 ㅎ
https://m.blog.naver.com/ndb796/221230967614

Java Code

package com.example.boj;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
import java.util.StringTokenizer;

public class Q1197 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        // i번째 노드의 부모를 저장
        // 인덱스: 노드
        // 값: 부모
        int[] parent = new int[n+1];
        for (int i=0;i<parent.length;i++) {
            parent[i] = i;
        }
        // 가중치로 정렬을 위해 우선순위 큐 사용 (Comparable-compareTo 구현)
        Queue<Node> pq = new PriorityQueue<>();
        int x=0,y=0,w=0;
        for (int i=0; i<m;i++) {
            st = new StringTokenizer(br.readLine());
            x = Integer.parseInt(st.nextToken());
            y = Integer.parseInt(st.nextToken());
            w = Integer.parseInt(st.nextToken());

            pq.offer(new Node(x, y, w));
        }

        int sum = 0;
        while (!pq.isEmpty()) {
            // 노드가 가중치로 정렬되었으므로 가중치가 가장 작은 간선부터 받아옴
            Node node = pq.poll();
            int a = find(parent, node.from);
            int b = find(parent, node.to);
            if (a != b) { // 같은 부모를 가지면 사이클 발생 (최소 비용 신장 트리 조건x)
                union(parent, a, b); // 부모가 다른 경우 두 노드를 합쳐줌
                sum += node.dis;
            }
        }
        System.out.println(sum);
        br.close();
    }
    // 자신의 루트부모노드를 찾는 함수
    public static int find(int[] parent, int x) {
        if (x == parent[x]) return x; // 종료조건 (부모와 같은 경우 부모를 찾은 것)
        return parent[x] = find(parent, parent[x]); // 자신의 부모의 부모를 찾기위해 재귀호출
    }
    // 부모노드를 함치는 함수 (같은 그래프에 속하도록 합치는 함수)
    public static void union(int[] parent, int x, int y) {
        // 합치고자 하는 두 개 노드의 부모를 찾음
        x = find(parent, x);
        y = find(parent, y);
        // 더 작은 노드로 합쳐줌
        if (x < y) parent[y] = x;
        else parent[x] = y;
    }

    static class Node implements Comparable<Node>{
        public int from;
        public int to;
        public int dis;

        public Node(int from, int to, int dis) {
            this.from = from;
            this.to = to;
            this.dis = dis;
        }

        @Override
        public int compareTo(Node node) {
            return dis - node.dis;
        }
    }
}

👍 Reference
안경잡이개발자 님 블로그
https://m.blog.naver.com/ndb796/221230967614