문제

https://www.acmicpc.net/problem/15736

게임을 진행할 차례인 학부에서 출전한 선수들 N명이 존재한다. 학생들의 앞 탁자에는 N개의 깃발이 청색이 위로 백색이 아래로 보이도록 놓여있다.

이때 출전한 선수 중 첫 번째 선수는 N개의 깃발 중 1의 배수에 해당하는 번호의 깃발을 뒤집어 놓는다. 다음 두 번째 선수는 N개의 깃발 중 2의 배수에 해당하는 번호의 깃발을 뒤집어 놓는다. i 번째 선수는 i의 배수에 해당하는 번호의 깃발을 뒤집고, N 번째 선수까지 진행하면 끝이 난다.

그렇다면 이 게임에서 N 명의 선수가 참가하고 N개의 깃발이 존재할 때, N 번째 선수까지 진행하여 완료된 상태에서 백색이 위로 놓여있는 깃발의 수가 몇 개인지 알아보자.

상황 : 1번 선수부터 N번 선수까지 차례대로 자기번호의 배수에 해당하는 깃발을 뒤집는다
원하는 것 : 백색이 위로 놓여있는 깃발의 수를 구하고 싶다

풀이과정

일단, 완전탐색을 할 수 있나 알아보자.

첫 번째 줄에 출전한 학생의 수이자, 깃발의 개수인 N(1 ≤ N ≤ 2,100,000,000)이 주어진다.

입력값이 최대 21억으로 시뮬레이션을 돌렸다간 21억 by 21억 배열을 만들어서 해야하는데 메모리가 터져버리고 말 것 이다. 물론 계산도.. 주어진 시간이 1초이니까 최소 1억번을 계산해야하는데 완전탐색은 불가능한 이야기다.

그러면 어떻게 해야할까? 일단 그림을 그려보자.

초기 상태: 청 청 청
1번째 선수: 백 백 백 (모든 깃발 뒤집기)
2번째 선수: 백 청 백 (2번째 깃발 뒤집기)
3번째 선수: 백 청 청 (3번째 깃발 뒤집기)

초기 상태: 청 청 청 청 청
1번째 선수: 백 백 백 백 백 (모든 깃발 뒤집기)
2번째 선수: 백 청 백 청 백 (2번째 깃발 뒤집기)
3번째 선수: 백 청 청 청 백 (3번째 깃발 뒤집기)
4번째 선수: 백 청 청 백 백 (4번째 깃발 뒤집기)
5번째 선수: 백 청 청 백 청 (5번째 깃발 뒤집기)

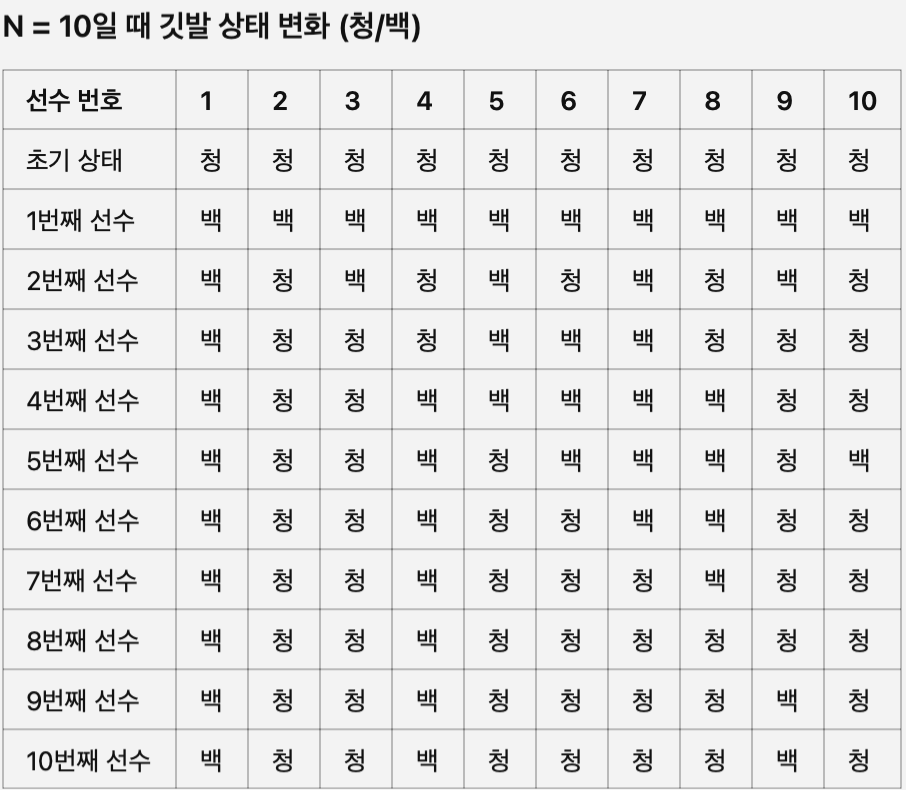
여기서 마지막 상태가 내가 원하는 상태인 백기 일 경우만 살펴보자.

1,4,9 번 깃발이 백기이다 이 깃발들은 홀수번 뒤집혔기 때문에 백기가 될 수 있었다.

왜 홀수냐? 간단하게 생각하자, 청기가 백기가 되려면 최소 1번은 뒤집어야 한다. 만약 청 -> 백 -> 청 -> 백 이렇게 다시 되돌아 오려면 3번 즉, 백기로 되돌아 오려면 홀수번을 뒤집어야 한다는 것을 이해할 수 있을 것이다.

그러면 우리가 원하는 백기가 되는 깃발들은 약수가 홀수개인 경우라고 할 수 있다. 일반적으로 약수의 개수는 짝수인 경우가 많다. 그럼 홀수인 경우는 어떻게 될까? 바로 제곱수인 경우이다.

약수의 특징을 살펴봐야 한다. 약수의 경우 일반적으로 짝을 이룬다.
8의 약수를 보자 (1,8) (2,4) 약수 네개가 모두 짝을 이루고 있다. 서로를 곱하면 8이 되는 형태로 하지만 제곱수의 경우 다르다.

9의 약수를 보자 (1,9) (3,3) 즉, 제곱근은 자기자신과 짝을 이루고 있기 때문에 약수의 개수가 홀수 인 것이다.

다시 문제로 돌아가서, 우리가 할 것은 간단하다 바로 N보다 작은 수 중 제곱수인 수의 개수 를 구하면 되는 것이다.

코드

import java.io.InputStreamReader;
import java.util.Scanner;

/**
 * @author onyoo
 * @performance
 * @category
 * @note
 * @see
 * @since 10/7/24
 **/
public class bj15736 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(new InputStreamReader(System.in));
		int N = sc.nextInt();
		
		int result = 0;
		for(int i=1;i<=N;i++){
			if(Math.pow(i,2) <= N){
				result ++;
			}else{
				break;
			}
		}

		System.out.println(result);
	}
}