선형회귀분석

단순 선형회귀 분석

회귀(Regression)

• 독립변수(x)로 종속변수(y)를 예측하는 것

독립변수 (Independent variable)

• 영향을 미칠 것으로 생각되는 변수

종속변수 (Dependent variable)

• 영향을 받을 것으로 생각되는 변수

회귀계수 (Coefficient)

• 기울기와 절편

다중 선형회귀분석

• 여러 원인이 존재하는 경우에 대해 여러 독립변수를 준비하고 종속변수 y를 설명하는 회귀 방정식을 만들어야 한다.
• 다중 회귀분석은 하나의 결과를 여러 원인으로 설명하기 위한 분석방법이다.
• 각 계수를 결정해야 한다

결정계수(R-squared)

• 독립변수가 종속변수를 얼마만큼 설명해주는지 가리키는 지표
• 0.5라고 하면 독립변수가 종속변수의 50%정도를 설명한다고 함
• 몇 펴센트 이상이 실질적으로 유용하다고 말하기는 어렵고 어떤분야냐에 따라 다름, 다만 일반적으로 20%이상
• SSE(Explained Sum of Squares) : 추정값에서 관측값의 평균을 빼고 총 합
• SSR(Residual Sum of Squares) : 관측값에서 추정값을 뺀, 잔차의 총 합
• SST(Total Sum of Squares) : 관측값에서 관측값의 평균을 뺀 결과의 총 합

선형회귀의 기본적인 가정 5가지

오차(Error)

• 모집단에서 회귀식을 얻어서 회귀식을 통해 얻은 예측값과 관측값의 차이

잔차(Residual)

• 표본집단에서 회귀식을 얻어서 회귀식을 통해 얻은 예측값과 관측값의 차이

선형성(Linearity)

• 종속변수 y와 독립변수 x간 선형적이어야 한다.

잔차 정규성(Normality)

• 잔차는 정규분포를 이루어야 한다.

독립성(independence)

• 다중 선형회귀에만 해당하는 가정
• 독립변수는 x 들은 서로 독립적이어야한다.
• 다중 공선성과 밀접하게 연관되어 있다.

다중 공선성(Multicollinearity)

• 다중 회귀분석을 수행할 경우 독립변수 간에 강한 상관관계(보통 0.6이상)가 없어야 한다.

등분산성(Homoskedasticity)

• 분산이 특정 패턴이 없이 일정해야 한다.

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.api as sm
from math import sqrt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from statsmodels.stats.outliers_influence import variance_inflation_factor
# 데이터 불러오기
dataset = datasets.load_boston()
# 데이터와 타겟데이터를 데이터프레임으로 변환
df_x = pd.DataFrame(dataset.data, columns=dataset.feature_names)
df_y = pd.DataFrame(dataset.target, columns=['MEDV'])
# 데이터와 타겟데이터를 병합
df = pd.concat([df_x, df_y], axis=1)
# pairplot 그리기
sns.pairplot(df[df.columns.values.tolist()]) 
plt.show()

다중 선형회귀

# MinMaxScaler() -> 0~1의 값으로 정규화
min_max_scaler = preprocessing.MinMaxScaler()
scale_columns = ['CRIM', 'ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
df_x[scale_columns] = min_max_scaler.fit_transform(df_x[scale_columns])
# test size를 20퍼로
train_X, test_X, train_y, test_y = train_test_split(df_x, df_y, test_size=0.3)
print(len(train_X), len(test_X), len(train_y), len(test_y) )
# 다중 선형회귀 돌리는 식
m_reg = sm.OLS(train_y, train_X).fit()
print(m_reg.summary())
# 데이터 예측하기
pred_y = np.array(m_reg.predict(test_X))
pred_y = pred_y.reshape(pred_y.shape[0],1)
test_y = np.array(test_y)
# MSE에 루트 씌워서 RMSE만들기
print(sqrt(mean_squared_error(test_y, pred_y)))
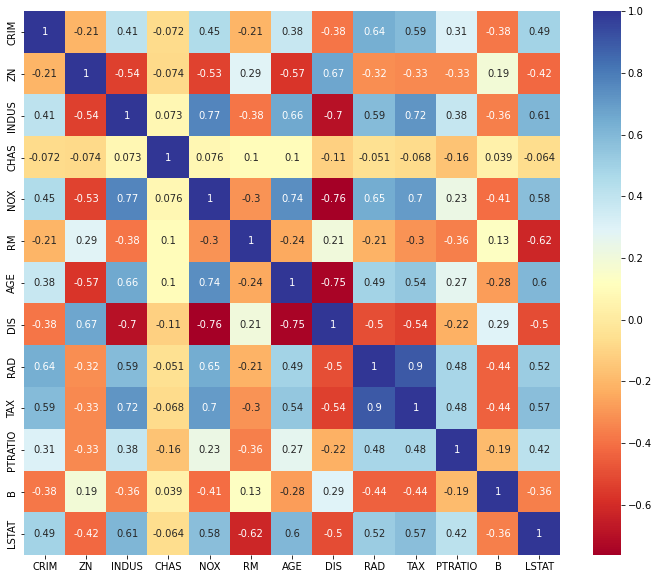
plt.figure(figsize=(12,10))
sns.heatmap(train_X.corr(), annot = True, cmap= 'RdYlBu')
plt.show()
# 1이나 -1에 가까운 값은 서로 상관관계가 있다

다중공산성

# 다중 공산성 구하기
# vif가 10을 넘어가면 다중 공산성이 있다고 판단
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(train_X.values, i) for i in range(train_X.shape[1])]
vif["features"] = train_X.columns
vif
# 공산성이 높은 요소 제거
tmp_train_X1 = train_X.drop('TAX', axis=1)
vif = pd.DataFrame()
vif["VIF Factor"] = [variance_inflation_factor(tmp_train_X1.values, i) for i in range(tmp_train_X1.shape[1])]
vif["features"] = tmp_train_X1.columns
# 다중 선형회귀
train_x_tmp = train_X[vif['features'].tolist()]
m_reg = sm.OLS(train_y, train_x_tmp).fit()
print(m_reg.summary())
# 반복...하고 그래프 그리기
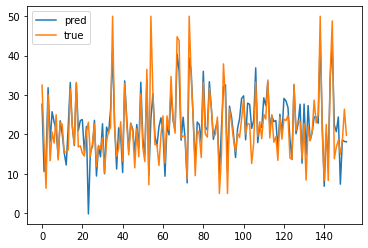
plt.plot(pred_y, label = "pred")
plt.plot(test_y, label = "true")
plt.legend()
plt.show()