[모두가 기술 면접에 합격하는 그날까지]
https://github.com/Lee-Jin-Hyeok/technical-interview-question
목차
- 그래프란?
1-1. 선형 자료구조 vs 비선형 자료구조 - 그래프의 용어
2-1. 그래프(Graph) vs 트리(Tree) - 그래프의 종류
3-1. 방향성이 있는가?
3-2. 가중치가 있는가?
3-3. 사이클이 있는가?
3-4. 완전 그래프 - 그래프의 구현
4-1. 인접 행렬을 이용한 구현 방법
4-2. 인접 리스트를 이용한 구현 방법 - 그래프의 사용
5-1. 그래프의 탐색
5-2. 최소 신장 트리 - 마무리
1. 그래프란?
그래프는 자료가 저장되어 있는 정점들과
이들을 연결하는 간선들의 집합으로 이루어지는
자료구조라고 할 수 있습니다.
일반적으로 생각할 수 있는 '막대그래프', '꺾은선 그래프'와 같은 차트(Chart)형식이 아니라
프로그래밍에서 사용되는 대표적인 비선형 자료구조 중 하나입니다.
1-1. 선형 자료구조 vs 비선형 자료구조
선형 자료구조의 대표적인 예로는 스택(Stack)과 큐(Queue)가 있고
비선형 자료구조의 대표적인 예로는 그래프(Graph)와 트리(Tree)가 있습니다.
비선형 자료구조에 대해서 알아보기 전에 선형 자료구조에 대해서 알아보자면,
선형 자료구조는 N번째 원소를 탐색하고 다음 원소를 탐색할 때
다음으로 탐색할 원소로 지정될 수 있는 원소가 일반적으로 하나인 자료구조를 말합니다.
따라서 비선형 자료구조는 N번째 원소를 탐색하고 다음 원소를 탐색할 때
다음으로 탐색할 원소로 지정될 수 있는 원소가 여러 개일 수 있는 자료구조를 말합니다.
따라서 그래프는 비선형 자료구조라는 것을 알 수 있습니다.
2. 그래프의 용어
그래프를 면접 질문에서 맞닥뜨리거나 공부를 하면서 그래프와 관련된 알고리즘을 만났을 때
그래프의 용어를 정확히 이해하지 못한다면 면접 질문에서 답변의 질이 떨어지거나,
알고리즘을 제대로 이해하지 못하는 경우가 생길 수도 있습니다.
따라서 그래프의 용어를 모두 외우지는 못하더라도 이들을 아는 것은 큰 도움이 될 것입니다.
그래프의 용어는 생각보다 많습니다.
하지만 그만큼 사용하지 않는 용어도 많습니다.
그래서 이번에는 그래프에서 사용되는 핵심적인 용어들을 정리하고자 합니다.
-
정점(Vertex)
그래프에서 자료를 담고 있는 원소를 모두 정점이라고 합니다.
그래프는 정점과 간선으로 이루어진 자료구조이므로 정점은 굉장히 중요한 개념입니다.
정점은 때론 노드(Node)라고도 불리기도하므로 혼동에 유의해야 합니다.따라서 위의 그래프 그림에서는 총 5개의 정점이 존재하고
각각 정점 A, 정점 B ... 등으로 불립니다. (물론 부르는 것에 규칙은 없습니다.)
-
간선(Edge)
간선은 정점 두 개를 연결하는 연결선의 역할을 합니다.
때론 링크(Link)라고도 불립니다. -
차수(Degree)
차수는 하나의 정점과 연결되어 있는 간선의 갯수를 말합니다.
아래에서 다시 소개하겠지만 방향성이 존재하지 않는
무향 그래프(무방향 그래프)에서 존재하는 개념으로,
유향 그래프에서는 진입 차수(In-Degree)와 진출 차수(Out-Degree)이라는
개념으로 대체합니다.흔히 차수 대신 'Degree'를 그대로 발음하여 '디그리'라고 부르는 경우가 많습니다.
-
사이클(Cycle)
그래프에서 같은 간선을 한 번만 거치고 순회하는데
같은 정점을 두 번 이상 방문한 경우 본 그래프에 '사이클'이 존재한다고 합니다.
이는 오히려 글로 풀어 쓰려면 힘든 개념입니다.
그래프를 딱 봤을 때 원이 그려지면 사이클이 존재하는 그래프입니다.사이클이 존재하지 않은 그래프를 트리(Tree)라고 하며
그래프와 같이 비선형 자료구조의 대표적인 자료구조입니다.사이클(Cycle) 대신 루프(Loop)라고도 할 수 있는데,
그래프에서의 루프는 다른 뜻도 포함할 수 있기 때문에
사이클이라고 표현하는 것이 좋을 것 같습니다.
-
자기 참조, 자기 루프(Self-Loop, Loop)
어떠한 정점의 간선이 자기 자신과 연결되어 있을 경우
이를 Self-Loop라고 합니다.'자기 참조'와 같이 한글이 아닌 'Self-Loop'를 그대로 발음하여
보통 '셀프-루프'라고 합니다.
-
경로(Path)
'경로'라는 뜻에서 알 수 있듯이
그래프에서 정점들을 간선을 통해 지나다니면서 생기는 경로를 말합니다.- Simple Path
Simple Path는 Path를 구성하는 정점들을 지나다니는 간선이
겹치지 않는 Path를 말합니다. - Elementary Path
Elementary Path는 Path를 구성하는 정점이 겹치지 않는 Path를 말합니다.
- Simple Path
2-1. 그래프(Graph) vs 트리(Tree)
그래프와 트리는 분명히 차이가 있지만 차이를 명확히 대답하지 못하는 경우가 있기도 합니다.
그래프와 트리의 차이는 사이클(Cycle)의 유무에 있습니다.
사이클이 존재하면 그냥 그래프인 것이고, 사이클이 존재하면 트리인 것입니다.
트리는 부모 노드에서 자식 노드로 향하는 단방향 간선을 가지고 있지만
그래프는 그러한 제한이 존재하지 않습니다.
그러므로 트리는 그래프의 한 종류로써, 트리가 그래프의 부분집합이라는 것을 알 수 있습니다.
3. 그래프의 종류
그래프에는 방향성이 있는가에 따라서, 가중치가 있는가에 따라서, 사이클이 있느냐에 따라서
그래프의 종류를 나눌 수 있고 이를 혼합하여 다양한 그래프를 만들 수 있습니다.
3-1. 방향성이 있는가?
정점과 정점을 연결하는 간선이 들어가고 나오는 방향이 존재할 경우
'간선에 방향성이 있다'라고 하고 이러한 간선을 가지는 그래프를
'방향성이 있는 그래프', '유향 그래프' 등으로 부릅니다. (Directed Graph)
반대의 경우를 '무향 그래프'라고 합니다. (Undirected Graph)
위의 그림처럼 간선의 끝부분에 화살표 형식으로 방향이 존재하는 그래프를
유향 그래프라고 합니다.
유향 그래프의 경우 방향이 존재하기 때문에 정점과 정점 사이에 간선이 연결되어 있다고 해서
무조건 이동할 수 있는 것이 아닙니다.
화살표의 방향에 따라 '단방향 간선'과 '양방향 간선'으로 나뉘는데
단방향 간선이 존재하기 때문에 무향 그래프와 다르게 Path를 만드는데
간선의 종류도 고려해야 한다는 특징이 있습니다.
A -> C (불가능), A -> B -> C (가능)
3-2. 가중치가 있는가?
기존에 위의 그래프의 경우에는 간선 간의 차이가 존재하지 않기 때문에
A 정점에서 D 정점까지 갈 수 있는 최단 거리 Path를 구하시오! 라고 한다면
답은 A -> B -> D 또는 A -> C -> D가 될 것입니다.
하지만 '가중치 그래프(Weighted Graph)'의 경우에는 간선에 가중치가 존재할 수 있습니다.
쉽게 생각하면 정점과 정점 사이의 거리가 정해졌다고 생각하면 좋습니다.
간선의 가중치는 간단하게 '가중치'라고도 하고 '코스트(Cost)'라고도 합니다.
다음 그림은 위의 그림에서 가중치를 적용한 가중치 그래프입니다.
만약 위와 같은 문제가 주어진다면 답은 A -> C -> D가 될 것입니다.
왜냐하면 A -> B -> D로 가는 코스트는 3 + 5로 8이지만
A -> C -> D로 가는 코스트는 6 + 1로 7이기 때문입니다.
유향/무향 그래프와 가중치 그래프는 같이 공존할 수 있습니다.
그럴 경우 부르는 이름은 정해져 있지는 않지만
'유향 가중치 그래프' 등으로 부를 수 있을 것 같습니다.
3-3. 사이클이 있는가?
그래프에는 사이클(Cycle)이 존재할 수도, 존재하지 않을 수도 있습니다.
사이클이 존재할 경우 '순환 그래프',
존재하지 않을 경우 '비순환 그래프'라고 합니다.
3-4. 완전 그래프(Complete Graph)
완전 그래프는 모든 정점이 다른 모든 정점과 연결되어 있는 그래프를 말합니다.
따라서 다음과 같은 그래프를 '완전 그래프'라고 말합니다.
무향 그래프의 경우 간선의 갯수가
((정점의 갯수) * ((정점의 갯수) - 1)) / 2
라는 특징을 가지고 있다.
4. 그래프의 구현
그래프를 구현하는 방법은 크게 '인접 행렬'과 '인접 리스트'가 있습니다.
4-1. 인접 행렬을 이용한 구현 방법
인접 행렬은 정점으로부터 인접한 정점들을 표기해놓은 표(행렬)입니다.
그럼 인접 행렬을 소개하기 위햇거 다음과 같은 그래프가 존재한다고 합시다.
이때 인접 행렬은 다음과 같이 만들어질 수 있습니다.
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 0 | 1 |
| C | 1 | 1 | 0 | 0 | 0 |
| D | 1 | 0 | 0 | 0 | 1 |
| E | 0 | 1 | 0 | 1 | 0 |
왼쪽에 있는 A, B, C, D, E 정점들이 갈 수 있는 위에 있는 정점에 대하여
1을 등록하고 가지 못하는 정점에 대해서는 0을 등록하여 만든 표라고 볼 수 있습니다.
무향 그래프의 경우 이 표가 왼쪽에서 내려오는 대각선 대칭이며,
유향 그래프의 경우에는 A -> B 일때 B -> A 임을 확신할 수 없으므로
대칭 형태가 이루어지지 않을 수도 있습니다.
또한 가중치가 있는 그래프의 경우에는 등록하는 값이 1또는 0이 아니라
그 가중치(코스트)를 등록합니다.
2차원 배열이라고 생각하면 쉽게 이해할 수 있습니다.
보통 실제로 구현할 때도 2차원 배열을 이용하여 구현합니다.
자기 자신으로 가는 경우에는 0으로 표기하는데
이는 자기 자신으로 가는 이유도 없을 뿐더러 가중치 그래프의 경우
0인 것이 바람직하기 때문이기도 합니다.
4-2. 인접 리스트를 이용한 구현 방법
인접 리스트는 하나의 정점을 기준으로 인접해있는 정점을
리스트 형태로 저장해서 구현하는 방법입니다.
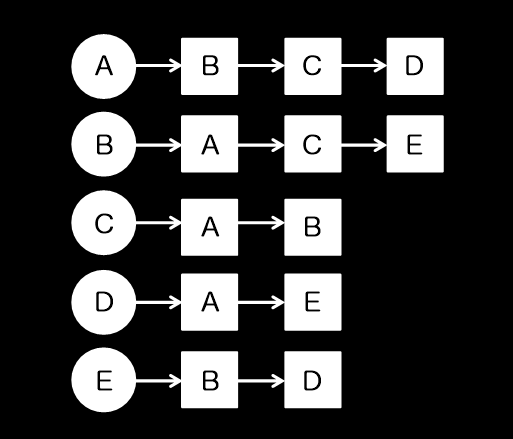
인접 행렬을 설명할 때 사용했던 그래프를 인접 리스트로 구현하면 위와 같이 만들어집니다.
이러면 A 정점이 어떤 정점으로 갈 수 있는지 한 눈으로 볼 수 있어서
인접 행렬보다 좋아보이기도 합니다.
A에서 B, C, D를 갈 수 있다는 것이지
A에서 B, B에서 C를 갈 수 있다는 뜻은 아닙니다.
5. 그래프의 사용
5-1. 그래프의 탐색
스택, 큐, 트리 등 다른 자료구조에서는 탐색을 시작하는 시작점이 분명히 존재하는 반면,
그래프의 경우에는 시작하는 점이 따로 존재하지 않습니다.
그래서 그래프를 탐색할 때에는 시작점을 사용자든, 개발자든, 의도에 맞춰서
시작점을 설정해주어야 합니다.
그래프를 탐색하는 방법에는 크게 DFS와 BFS가 존재합니다.
DFS는 Depth First Search의 약자로 한글로 번역하면 깊이 우선 탐색이라는 뜻입니다.
DFS는 인접 정점 중 어떠한 정점을 골라서 탐색하고,
또 그 정점의 인접 정점 중 하나를 골라서 탐색하는 식으로 진행되는 탐색방법입니다.
하지만 DFS는 그래프의 깊이가 무한이 깊을 경우 무한 루프에 빠질 가능성이 있는 알고리즘입니다.
BFS는 Breadth First Search의 약자로 한글로 번역하면 너비 우선 탐색이라는 뜻입니다.
BFS는 인접 정점을 모두 탐색한 뒤 하나의 인접 정점을 골라서
또 인접 정점을 모두 탐색하는 식으로 탐색하는 탐색방법입니다.
찾고자 하는 정점의 깊이가 깊을 경우 찾는데 오래 걸릴 수 있습니다.
5-2. 최소 신장 트리
최소 신장 트리를 만드는 과정에서 그래프가 사용됩니다.
그래프는 우리가 흔히 접할 수 있는 네비게이션과 같이 최단 경로를 찾아주는 시스템에 사용됩니다.
그런데 그래프에서 어떤 곳이 최단 경로인지 알 수 있도록 찾는 알고리즘이 필요한데,
알고리즘을 통해 만들어지는 그래프가 '최소 신장 트리'입니다.
최소 신장 트리(Minimum Spanning Tree)는 가장 최적의 경로만을 남긴 그래프를 말하는데요,
만들고 나서 결과물을 보면 트리이기 때문에 최소 신장 그래프가 아니라 최소 신장 트리라고 부릅니다.
이 최소 신장 트리를 만드는 알고리즘은 Prim, Dijkstra, Kruskal 등이 있습니다.
마무리
지금까지 그래프가 무슨 자료구조인지 알아보고,
용어, 종류, 구현방법, 사용처에 대해서 알아보았습니다.
개인적으로 그래프는 그래프 자체보다는
Prim, Dijkstra, Kruskal 알고리즘이 중요하다고 생각합니다.
특히 면접 질문에 많이 나오고 다른 라우터 프로토콜 등에도 자주 등장하는
Dijkstra 알고리즘이 중요하니 꼭 알아두시는 것을 추천드립니다.
또한 그래프 자체는 용어 정도만 정확히 익히고 있으면 된다고 생각합니다.
여기 나와있는 그래프의 용어는 일부에 불가하며
수많은 그래프의 용어가 존재합니다.
부족한 제 글을 읽어주셔서 감사합니다.
더 노력하는 개발자가 되도록 노력하겠습니다!!

