[모두가 기술 면접에 합격하는 그날까지]
https://github.com/Lee-Jin-Hyeok/technical-interview-question
목차
- 이분 탐색(Binary Search)란?
- 이분 탐색의 탐색 과정
- 이분 탐색의 특징
3-1. 장점
3-2. 단점 - 마무리
1. 이분 탐색(Binary Search)란?
이분 탐색은 정렬되어 있는 자료를 두 부분으로 나누어서 탐색하는 알고리즘입니다.
이분 탐색은 O(log n)의 시간 복잡도를 가지며, 이진 탐색이라고도 불립니다.
2. 이분 탐색의 탐색 과정
이분 탐색은 자료가 N개 있을 때 N/2번째 인덱스에 존재하는 자료와
찾고자 하는 자료를 비교하여 (오름차순 정렬일때) 찾고자 하는 자료가 더 크면
왼쪽을 버리고, 더 작으면 오른쪽을 버리면서 탐색합니다.
다음과 같은 자료의 구성이 존재할 경우 이분 탐색을 통해 8을 찾는 과정은 다음과 같습니다.
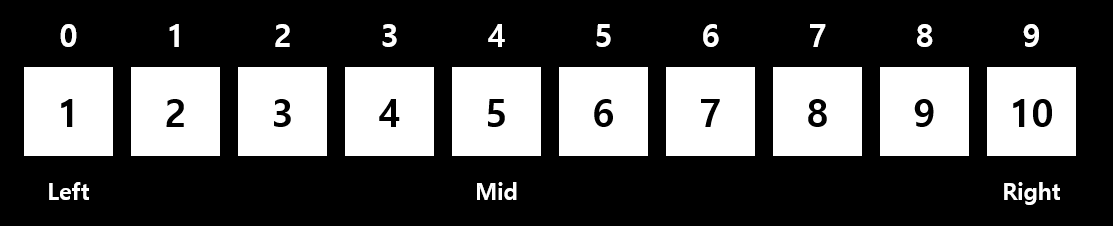
- 가장 왼쪽의 자료의 인덱스를 Left, 가장 오른쪽의 자료의 인덱스를 Right라고 두고,
(Left + Right) / 2한 인덱스를 Mide라고 둡니다.
찾고자 하는 값(8)보다 Mid의 값(5)가 더 작으므로,
인덱스 4 왼쪽에 있는 값들은 무시합니다.
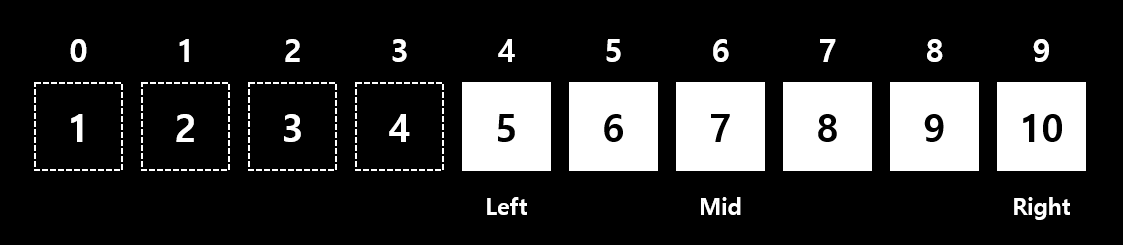
- 마찬가지로 찾고자 하는 값인 8보다 Mid의 값인 7이 작으므로,
인덱스 6 왼쪽에 있는 값들을 무시합니다.
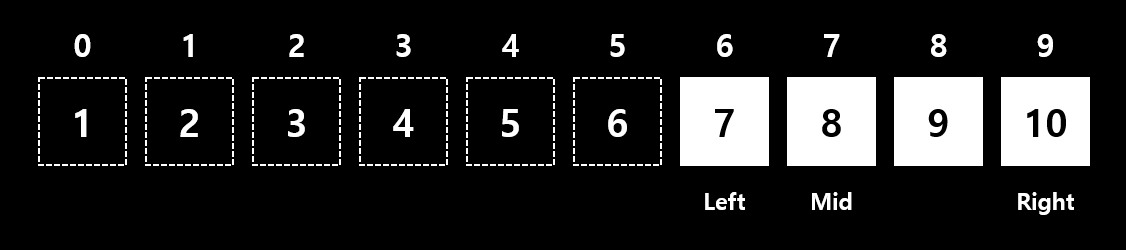
- 찾고자 하는 값과 Mid의 값이 같으므로 값을 찾았습니다.
이분 탐색은 이와 같은 방식으로 탐색을 진행합니다.
O(log n)의 시간 복잡도를 가지고 있기 때문에 순차 탐색에 비해서 훨씬 빠른 성능을 자랑합니다.
3. 이분 탐색의 특징
3-1. 장점
- 탐색 과정에서 봤던 것처럼 순차 탐색에 비해서 훨씬 빠른 성능을 자랑합니다.
- 구현하기가 간단합니다.
3-2. 단점
- 반드시 정렬되어 있어야 사용할 수 있는 알고리즘입니다.
4. 마무리
탐색하는 알고리즘 중 가장 혁신적이면서도 가장 간단한 알고리즘이었습니다.
C를 배우고 구현해봤던 기억이 있는 추억의 알고리즘이었던 것 같습니다.
제 글을 읽어주신 분들께 정말로 감사드립니다.
더 노력하는 개발자가 되도록 노력하겠습니다.

